Chapter 2: Highest common factor and lowest common multiple
2.1 Highest common factor
Factors
A factor is any of the two or more whole numbers we multiply to get a product. For example: . The numbers 6 and 2 are factors of 12.
A factor is also described as a whole number that divides into a larger number without a remainder. For example: . The number 6 divides perfectly into 12. Therefore, the number 6 is a factor of 12.
factor A factor is a whole number that divides into a larger number without a remainder.
Worked example 2.1: Factors
Find all the factors of the number 60.
-
Step 1: Any number larger than 1 has the number itself and 1 as factors.
-
Step 2: Start with 2 and see if it divides into 60 without a remainder.
-
Step 3: Try each consecutive number to see if it divides into 60 without a remainder. Stop when you get to a number that you already have as an answer.
\begin{array}{2} \frac{60}{3} = 20 \hspace{10mm} &3 \times 20 = 60 \newline \frac{60}{4} = 15 &4 \times 15 = 60 \newline \frac{60}{5} = 12 &5 \times 12 = 60 \newline \frac{60}{6} = 10 &6 \times 10 = 60 \newline \end{array}The numbers 7, 8 and 9 do not divide into 60 without a remainder, so they are not factors of 60.
You already have the number 10, as 60 divided by 6 is 10, so you can stop there.
-
Step 4: List all the factors from the smallest number to the largest number.
The factors of 60 are: 1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60
Exercise 2.1: Find factors
Find all the factors of the following numbers:
-
54
\begin{array}{2} \text{1 and itself} \hspace{10mm}&1 \times 54=54 \newline \frac{54}{2} = 27 &2 \times 27 = 54 \newline \frac{54}{3} = 18 &3 \times 18 = 54 \newline \frac{54}{6} = 9 & 6 \times 9 = 54 \newline \frac{54}{9} = 6 & \text{already divided} \end{array}
The factors of 54 are: 1; 2; 3; 6; 9; 18; 27; 54
-
39
\begin{array}{2} \text{1 and itself} \hspace{10mm}&1 \times 39=39 \newline \frac{39}{3} = 13 & 3 \times 13 = 39 \newline \frac{39}{13} = 3 & \text{already divided} \end{array}
The factors of 39 are: 1; 3; 13; 39
-
45
\begin{array}{2} \text{1 and itself} \hspace{10mm}&1 \times 45=45 \newline \frac{45}{3} = 15 & 3 \times 15 = 45 \newline \frac{45}{5} = 9 & 5 \times 9 = 45 \newline \frac{45}{9} = 5 & \text{already divided} \end{array}
The factors of 45 are: 1; 3; 5; 9; 15; 45
Prime factors
The number 3 has only two factors: 1 and 3. Similarly, the number 11 has only two factors: 1 and 11. These are examples of prime numbers.
prime number A prime number is a number that has only two factors: 1 and the number itself.
The prime numbers between 1 and 100 are highlighted in the grid below.
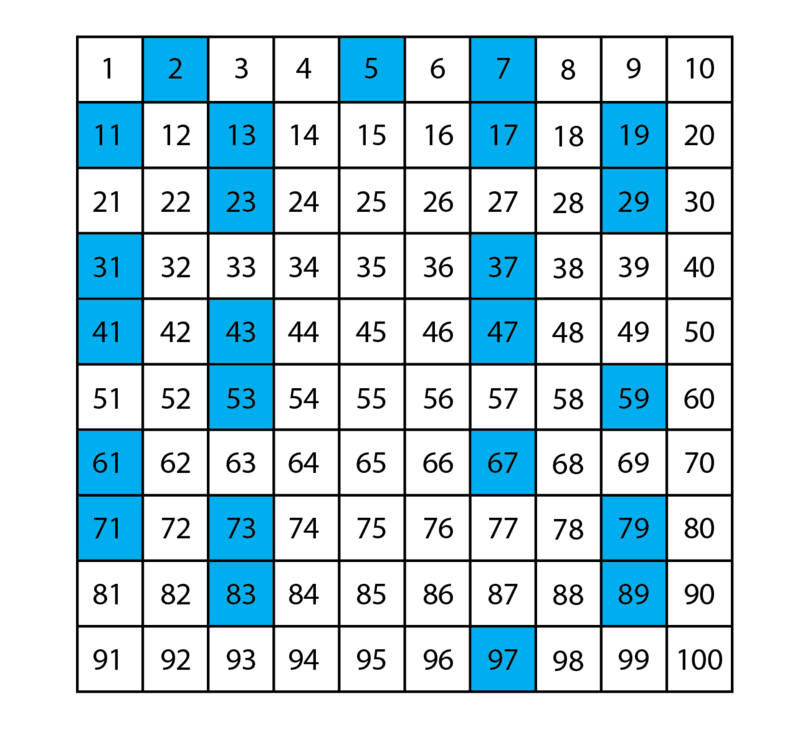
prime factors These are the factors of a number that are also prime numbers. Any non-prime number can be broken down into prime factors. We can then write the number as a product of its prime factors.
prime factor A prime factor is a factor that is also a prime number.
Worked example 2.2: Prime factors
Find the prime factors of 80.
-
Step 1: Find the smallest prime number that is a factor of 80. Express 80 as a product of two factors.
-
Step 2: Find the smallest prime number that is a factor of the non-prime factor from Step 1. Express 80 as a product of three factors.
-
Step 3: Repeat Step 2 until 80 is expressed as a product of only prime numbers.
Remember that 1 is not a prime number.
Exercise 2.2: Express numbers as products of prime factors
Express the following numbers as products of prime factors:
-
30
\begin{array}{2} & \frac{30}{2}=15 &\hspace{10 mm}30=2 \times 15 \newline & \frac{15}{3}=5 &\hspace{10mm} 30=2 \times 3 \times 5 \end{array}
-
140
\begin{array}{2} & \frac{140}{2}=70 &\hspace{10 mm}140=2 \times 70 \newline & \frac{70}{2}=35 &\hspace{10mm} 140=2 \times 2 \times 35 \newline & \frac{35}{5}=7 &\hspace{10mm} 140=2 \times 2 \times 5 \times 7 \newline \end{array}
-
195
\begin{array}{2} & \frac{195}{3}=65 &\hspace{10 mm}195=3 \times 65 \newline & \frac{65}{5}=13 &\hspace{10mm} 195=3 \times 5 \times 13 \newline \end{array}
-
252
\begin{array}{2} & \frac{252}{2}=126 &\hspace{10 mm}252=2 \times 126 \newline & \frac{126}{2}=63 &\hspace{10mm} 252=2 \times 2 \times 63 \newline & \frac{63}{3}=21 &\hspace{10mm} 252=2 \times 2 \times 3 \times 21 \newline & \frac{21}{3}=7 &\hspace{10mm} 252=2 \times 2 \times 3 \times 3 \times 7 \newline \end{array}
-
297
\begin{array}{2} & \frac{297}{3}=99 &\hspace{10 mm}297=3 \times 99 \newline & \frac{99}{3}=33 &\hspace{10mm} 297=3 \times 3 \times 33 \newline & \frac{33}{3}=11 &\hspace{10mm} 297=3 \times 3 \times 3 \times 11 \newline \end{array}
Index form
Finding and writing down the prime factors of large numbers can become confusing. To make the process easier, we may use continued division and write the prime factors in index form. The index or power of a number tells us how many times we multiply the number by itself. For example, means . In this case, 4 is the power or index of 2.
index form Index form tells you how many times to use the same number in a multiplication by writing a superscript next to the number, for example means multiply 3 by 3.
An index of 1 means a number is not multiplied by itself. Therefore, and have the same meaning.
Worked example 2.3: Prime factors in index form
Find the prime factors of 180 and write them in index form.
-
Step 1: Divide the smallest prime factor of 180 until it cannot divide any further.
\begin{array}{r | r} 2 & 180 \newline \hline 2 & 90 \newline \hline & 45 \end{array} -
Step 2: Move to the next prime factor of 180. Keep on dividing until it cannot divide any further.
\begin{array}{r | r} 2 & 180 \newline \hline 2 & 90 \newline \hline 3 & 45 \newline \hline 3 & 15 \newline \hline & 5 \end{array} -
Step 3: Repeat Step 2 until you get 1 as an answer.
\begin{array}{r | r} 2 & 180 \newline \hline 2 & 90 \newline \hline 3 & 45 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array} -
Step 4: Write down all the prime factors of 180. Use superscripts to write the index of each prime factor, that is, how many times the prime factor divided.
The index of each prime factor shows us how many times we must multiply each prime factor to get 180 again:
Exercise 2.3: Express numbers as products of prime factors in index form
Express the following numbers as prime factors in index form:
-
60
\begin{array}{r | r} 2 & 60 \newline \hline 2 & 30 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
-
144
\begin{array}{r | r} 2 & 144 \newline \hline 2 & 72 \newline \hline 2 & 36 \newline \hline 2 & 18 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array}
-
198
\begin{array}{r | r} 2 & 198 \newline \hline 3 & 99 \newline \hline 3 & 33 \newline \hline 11 & 11 \newline \hline & 1 \end{array}
-
300
\begin{array}{r | r} 2 & 300 \newline \hline 2 & 150 \newline \hline 3 & 75 \newline \hline 5 & 25 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
-
3 375
\begin{array}{r | r} 3 & 3\space 375 \newline \hline 3 & 1\space 125 \newline \hline 3 & 375 \newline \hline 5 & 125 \newline \hline 5 & 25 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
Common factors
Two numbers have a common factor if the same number is a factor of both numbers. For example, the number 2 divides into both 10 and 12 without a remainder. Therefore, 2 is a common factor of 10 and 12.
common factor A common factor is a factor of two or more numbers.
Worked example 2.4: Common factors
Find the common factors of 12 and 18.
-
Step 1: List all the factors for both numbers, from the smallest factor to the largest factor.
The factors of 12 are: 1; 2; 3; 4; 6; 12
The factors of 18 are: 1; 2; 3; 6; 9; 18 -
Step 2: Identify the numbers that appear in both lists.
The numbers 1, 2 and 3 are the common factors of 12 and 18.
The number 1 is a common factor of all whole numbers.
Exercise 2.4: Find common factors
Find the common factors of the following sets of numbers:
-
15 and 27
The factors of 15 are: 1; 3; 5; 15
The factors of 27 are: 1; 3; 9; 27The common factors are 1 and 3.
-
30 and 45
The factors of 30 are: 1; 2; 3; 5; 6; 10; 15; 30
The factors of 45 are: 1; 3; 5; 9; 15; 45The common factors are 1, 3, 5 and 15.
-
10, 20 and 30
The factors of 10 are: 1; 2; 5; 10
The factors of 20 are: 1; 2; 4; 5; 10; 20
The factors of 30 are: 1; 2; 3; 5; 6; 10; 15; 30The common factors are 1, 2, 5 and 10.
The highest common factor (HCF) of two numbers is the largest number that is a factor of both. For example, the common factors of 12 and 16 are 1, 2 and 4. The number 4 is the largest number on the list, so it is the highest common factor.
highest common factor (HCF) The highest common factor is the largest whole number that divides into two or more numbers without a remainder.
Exercise 2.5: Find the HCF
In Exercise 2.4, you determined the common factors of the following sets of numbers. Now identify the HCF in each case.
-
15 and 27
The common factors are 1 and 3.
HCF = 3 -
30 and 45
The common factors are 1, 3, 5 and 15.
HCF = 15 -
10, 20 and 30
The common factors are 1, 2, 5 and 10.
HCF = 10
Worked example 2.5: HCF using prime factors
Find the HCF of 60 and 80.
-
Step 1: Express each number as a product of prime factors.
\begin{array}{r | r} 2 & 60 \newline \hline 2 & 30 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 80 \newline \hline 2 & 40 \newline \hline 2 & 20 \newline \hline 2 & 10 \newline \hline 5 & 5 \newline \hline & 1 \end{array} -
Step 2: Identify all the prime factors that are contained in both numbers.
The number 2 appears twice for 80 and 60:
The number 3 does not appear for 80
The number 5 appears once for 80 and 60: -
Step 3: Multiply the prime factors you identified to get the HCF.
Worked example 2.6: HCF using prime factors in index form
Find the HCF of 90 and 108.
-
Step 1: Express each number as a product of prime factors in index form.
\begin{array}{r | r} 2 & 90 \newline \hline 3 & 45 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 108 \newline \hline 2 & 54 \newline \hline 3 & 27 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} -
Step 2: Identify the prime factors that are contained in both numbers, to the lowest index.
The number 2 divided into both 90 and 108. The lowest index both numbers have as a factor is one:
The number 3 divided into both 90 and 108. The lowest index both numbers have as a factor is two: -
Step 3: Multiply the prime factors you identified to get the HCF.
Exercise 2.6: Use different methods to find the HCF
-
For the following sets of numbers, find all the factors of each number and then find the HCF.
- 15 and 80
Factors of 15: 1; 3; 5; 15
Factors of 80: 1; 2; 4; 5; 8; 10; 16; 20; 40; 80
HCF = 5
- 40 and 64
Factors of 40: 1; 2; 4; 5; 8; 10; 20; 40
Factors of 64: 1; 2; 4; 8; 16; 32; 64
HCF = 8
- 50 and 70
Factors of 50: 1; 2; 5; 10; 25; 50
Factors of 70: 1; 2; 5; 7; 10; 14; 35; 70
HCF = 10
- 18, 24 and 32
Factors of 18: 1; 2; 3; 6; 9; 18
Factors of 24: 1; 2; 3; 4; 6; 8; 12; 24
Factors of 32: 1; 2; 4; 8; 16; 32
HCF = 2
- 30, 45 and 75
Factors of 30: 1; 2; 3; 5; 6; 10; 15; 30
Factors of 45: 1; 3; 5; 9; 15; 45
Factors of 75: 1; 3; 5; 15; 25; 75
HCF = 15
-
For the following sets of numbers, express each number as a product of prime factors and then find the HCF.
- 39 and 169
\begin{array}{r | r} 3 & 39 \newline \hline 13 & 13 \newline \hline & 1 \end{array} \begin{array}{r | r} 13 & 169 \newline \hline 13 & 13 \newline \hline & 1 \end{array}
HCF = 13
- 45 and 63
\begin{array}{r | r} 3 & 45 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 3 & 63 \newline \hline 3 & 21 \newline \hline 7 & 7 \newline \hline & 1 \end{array}
- 144 and 216
\begin{array}{r | r} 2 & 144 \newline \hline 2 & 72 \newline \hline 2 & 36 \newline \hline 2 & 18 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 216 \newline \hline 2 & 108 \newline \hline 2 & 54 \newline \hline 3 & 27 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array}
- 28, 42 and 70
\begin{array}{r | r} 2 & 28 \newline \hline 2 & 14 \newline \hline 7 & 7 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 42 \newline \hline 3 & 21 \newline \hline 7 & 7 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 70 \newline \hline 5 & 35 \newline \hline 7 & 7 \newline \hline & 1 \end{array}
- 36, 63 and 72
\begin{array}{r | r} 2 & 36 \newline \hline 2 & 18 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 3 & 63 \newline \hline 3 & 21 \newline \hline 7 & 7 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 72 \newline \hline 2 & 36 \newline \hline 2 & 18 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array}
-
For the following sets of numbers, express each number as a product of prime factors in index form and then find the HCF.
- 36 and 120
\begin{array}{r | r} 2 & 36 \newline \hline 2 & 18 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 120 \newline \hline 2 & 60 \newline \hline 2 & 30 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
- 125 and 300
\begin{array}{r | r} 5 & 125 \newline \hline 5 & 25 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 300 \newline \hline 2 & 150 \newline \hline 3 & 75 \newline \hline 5 & 25 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
- 288 and 360
\begin{array}{r | r} 2 & 288 \newline \hline 2 & 144 \newline \hline 2 & 72 \newline \hline 2 & 36 \newline \hline 2 & 18 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 360 \newline \hline 2 & 180 \newline \hline 2 & 90 \newline \hline 3 & 45 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
- 32, 56 and 140
\begin{array}{r | r} 2 & 32 \newline \hline 2 & 16 \newline \hline 2 & 8 \newline \hline 2 & 4 \newline \hline 2 & 2 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 56 \newline \hline 2 & 28 \newline \hline 2 & 14 \newline \hline 7 & 7 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 140 \newline \hline 2 & 70 \newline \hline 5 & 35 \newline \hline 7 & 7 \newline \hline & 1 \end{array}
- 96, 160 and 224
\begin{array}{r | r} 2 & 96 \newline \hline 2 & 48 \newline \hline 2 & 24 \newline \hline 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 160 \newline \hline 2 & 80 \newline \hline 2 & 40 \newline \hline 2 & 20 \newline \hline 2 & 10 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 224 \newline \hline 2 & 112 \newline \hline 2 & 56 \newline \hline 2 & 28 \newline \hline 2 & 14 \newline \hline 7 & 7 \newline \hline & 1 \end{array}
2.2 Lowest common multiple
Multiples
Natural numbers are the numbers we use for counting. They include all the positive whole numbers from 1 onwards: . The multiples of a given number are the numbers you get when you multiply the given number with the natural numbers. For example, the multiples of the number 5 are:
A multiple is also described as a whole number into which a smaller number divides without a remainder. For example: . The number 6 divides perfectly into 12. Therefore, the number 12 is a multiple of 6.
multiple A multiple is a whole number into which a smaller number divides without a remainder.
Exercise 2.7: Find multiples
Write down the first five multiples of the following numbers.
-
8
The first five multiples are:
-
13
The first five multiples are:
-
21
The first five multiples are:
Common multiples
A multiple is a number that can be divided by another number without a remainder. Two numbers have a common multiple if the same number is a multiple of both those numbers. For example, the number 12 is a common multiple of the numbers 3 and 4. We know this because both 3 and 4 divide into 12 without a remainder.
common multiple A common multiple is a multiple of two or more numbers.
Worked example 2.7: Common multiples
Find three common multiples of 5 and 6.
-
Step 1: List the first ten multiples of each number.
The first ten multiples of 5 are:
The first ten multiples of 6 are: -
Step 2: Identify the numbers that appear in both lists.
The number 30 is the only number that appears in both lists.
-
Step 3: Expand the lists until you find another number that appear in both lists.
Multiples of 5:
Multiples of 6:The number 60 also appears in both lists.
-
Step 4: Repeat Step 3 until you find the required number of common multiples.
Multiples of 5:
Multiples of 6:The number 90 also appears in both lists.
-
Step 5: Write down the common multiples.
Three common multiples of 5 and 6 are:
An easy way to find a common multiple of two or more numbers is to multiply the numbers. For example, . This tells us that 30 is a common multiple of 5 and 6. If you multiply 30 two more times, you get 60 and then 90, which gives you the three common multiples required.
Exercise 2.8: Find common multiples
Find two common multiples of the following sets of numbers:
-
12 and 15
Multiples of 12:
Multiples of 15:
Common multiple: 60
Common multiple: 180Two common multiples of 12 and 15 are:
-
5, 10 and 15
Multiples of 5:
Multiples of 10:
Multiples of 15:
Common multiple: 30
Common multiple: 750Two common multiples of 5, 10 and 15 are:
-
2, 4 and 6
Multiples of 2:
Multiples of 4:
Multiples of 6:
Common multiple: 12
Common multiple: 48Two common multiples of 2, 4 and 6 are:
The lowest common multiple (LCM) of two numbers is the smallest number that is a multiple of both. For example, the first three common multiples of the numbers 4 and 6 are 12, 24 and 36. The number 12 is the smallest of these multiples.
lowest common multiple (LCM) The lowest common multiple is the smallest whole number into which two or more numbers divide without a remainder.
Exercise 2.9: Find the LCM
In Exercise 2.8, you determined two common multiples of the following sets of numbers. Now identify the LCM in each case.
-
12 and 15
Multiples of 12:
Multiples of 15: -
5, 10 and 15
Multiples of 5:
Multiples of 10:
Multiples of 15: -
2, 4 and 6
Multiples of 2:
Multiples of 4:
Multiples of 6:
Worked example 2.8: LCM using prime factors
Find the LCM of 12 and 18.
-
Step 1: Express each number as a product of prime factors.
\begin{array}{r | r} 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 18 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} -
Step 2: Identify all the prime factors that must be included in a common multiple.
Any multiple of 12 must contain: (The factor is included in ; see next line)
Any multiple of 18 must contain: (The factor is included in ; see previous line)A multiple that contains automatically contains . Similarly, a multiple that contains automatically contains .
-
Step 3: Multiply the prime factors that have to be included in both multiples to get the LCM.
Worked example 2.9: LCM using prime factors in index form
Find the LCM of 60 and 45.
-
Step 1: Express each number as a product of prime factors in index form.
\begin{array}{r | r} 2 & 60 \newline \hline 2 & 30 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 3 & 45 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array} -
Step 2: List all the prime factors that were used, to the highest index.
The factor 2 was used and its highest index is two:
The factor 3 was used and its highest index is two:
The factor 5 was used: -
Step 3: Multiply the prime factors you listed to get the LCM.
Exercise 2.10: Use different methods to find the LCM
-
For the following sets of numbers, use lists of multiples to find the LCM.
- 6 and 21
Multiples of 6:
Multiples of 21:- 4 and 11
Multiples of 4:
Multiples of 11:- 7 and 9
Multiples of 7:
Multiples of 9:- 2, 3 and 5
Multiples of 2:
Multiples of 3:
Multiples of 5:- 6, 10 and 12
Multiples of 6:
Multiples of 10:
Multiples of 12: -
For the following sets of numbers, express each number as a product of prime factors and then find the LCM.
- 9 and 12
\begin{array}{r | r} 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array}
Any multiple of 9 must contain:
Any multiple of 12 must contain: ( is included in )- 20 and 50
\begin{array}{r | r} 2 & 20 \newline \hline 2 & 10 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 50 \newline \hline 5 & 25 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
Any multiple of 20 must contain: ( is included in below)
Any multiple of 50 must contain: ( is included in above)- 24 and 40
\begin{array}{r | r} 2 & 24 \newline \hline 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 40 \newline \hline 2 & 20 \newline \hline 2 & 10 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
Any multiple of both 24 and 40 must contain:
Any multiple of 24 must contain:
Any multiple of 40 must contain:- 6, 8 and 12
\begin{array}{r | r} 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 8 \newline \hline 2 & 4 \newline \hline 2 & 2 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array}
Any multiple of 6 must contain: ( is included in below)
Any multiple of 8 must contain:
Requirements for multiples of 12 are already listed ( is included in ; listed for the number )- 10, 16 and 18
\begin{array}{r | r} 2 & 10 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 16 \newline \hline 2 & 8 \newline \hline 2 & 4 \newline \hline 2 & 2 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 18 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array}
Any multiple of 10 must contain: ( is included in below)
Any multiple of 16 must contain:
Any multiple of 18 must contain: ( is included in above) -
For the following sets of numbers, express each number as a product of prime factors in index form and then find the LCM.
- 12 and 27
\begin{array}{r | r} 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 3 & 27 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array}
- 20 and 25
\begin{array}{r | r} 2 & 20 \newline \hline 2 & 10 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 5 & 25 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
- 24 and 28
\begin{array}{r | r} 2 & 24 \newline \hline 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 28 \newline \hline 2 & 14 \newline \hline 7 & 7 \newline \hline & 1 \end{array}
- 9, 12 and 15
\begin{array}{r | r} 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
- 48, 72 and 120
\begin{array}{r | r} 2 & 48 \newline \hline 2 & 24 \newline \hline 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 72 \newline \hline 2 & 36 \newline \hline 2 & 18 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 120 \newline \hline 2 & 60 \newline \hline 2 & 30 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
2.3 Compare HCF and LCM
Be careful to not confuse HCF and LCM. The differences are listed in the table.
| HCF (highest common factor) | LCM (lowest common multiple) |
|---|---|
| A factor of two or more numbers | A multiple of two of more numbers |
| HCF must divide into the given numbers | Given numbers must divide into LCM |
| Only common prime factors to lowest index | All prime factors to highest index |
| Smaller than or equal to given numbers | Larger than or equal to given numbers |
Worked example 2.10: HCF and LCM
Find the HCF and the LCM of 24 and 32.
-
Step 1: Express each number as a product of prime factors in index form.
\begin{array}{r | r} 2 & 24 \newline \hline 2 & 12 \newline \hline 2 & 6 \newline \hline 3 & 3 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 32 \newline \hline 2 & 16 \newline \hline 2 & 8 \newline \hline 2 & 4 \newline \hline 2 & 2 \newline \hline & 1 \end{array} -
Step 2: For the HCF, identify the common prime factors to the lowest index. For the LCM, list all the prime factors to the highest index.
| HCF | LCM |
|---|---|
| Largest number that can divide into 24 and 32 | Smallest number into which 24 and 32 can divide |
Exercise 2.10: Determine HCF and LCM
The prime factorisation of three numbers are as follows:
-
Determine the LCM of the three numbers.
-
Determine the HCF of the three numbers.
-
Apart from the HCF, identify another common factor for the three numbers.
-
Calculate the three original numbers.
2.4 Practical applications
You can use your knowledge of factors and multiples to solve problems. Here are some hints:
- Decide whether the problem is about factors or multiples. Factors divide into a given number. Multiples are the products of a given number and the natural numbers.
- If you have to divide two or more amounts into smaller units, finding the HCF might solve the problem.
- If you have to find a larger amount from smaller units, finding the LCM might solve the problem.
- When you get stuck, list all the factors, or list the first ten multiples of the given numbers. Try to connect the lists to the question.
Exercise 2.11: Use factors and multiples to solve problems
-
Chinasa is a student. This year, her age is a multiple of 6. Next year, her age will be a multiple of 5. If Chinasa is younger than 40, how old will she be next year?
Multiples of 6 smaller than 40:
Multiples of 5 smaller than 40:Her age next year must be one more than her age this year. The number 25 (a multiple of 5) is one more than the number 24 (a multiple of 6).
Therefore, she will be 25 next year.
-
Zahrah decides to sell sweets for extra pocket money. She buys a bag of chocolate bars and a bag of toffees. At home, she opens the bags and discovers that she has 24 chocolate bars and 80 toffees. She decides to make up smaller packets to sell. She divides all the sweets into packets that have equal amounts of chocolate bars and toffees. What is the maximum number of packets she can make up?
Find the largest number that can divide into 24 and 80, that is, the HCF.
Therefore, the maximum number of packets Zahrah can make up is 8.
-
It is school holidays. Suleiman, Umar and Faruq want to earn some pocket money. They decide to wash cars on the days that they do not have chores to do at home. Suleiman washes 4 cars per day and Uman washes 5 cars per day. Faruq is the fastest and washes 6 cars per day. At the end of the holidays, they find to their surprise that each of them washed the same total number of cars over the holidays.
- Determine the minimum number of cars each person could have washed over the holidays.
Find the smallest number that is a multiple of 4, 5 and 6, that is, the LCM.
- Calculate how many days of the school holidays each person washed cars.
Suleiman: days
Umar: days
Faruq: days
-
Chika's family has a few dogs and a few chickens. They have a total of 8 animals. The animals have 22 legs altogether. How many dogs and how many chickens does the family have?
\begin{array}{l r r r r r r r r} \text{number of chickens}\space\space&1&2&3&4&5&6&7 \newline \text{number of legs}\space\space&2&4&6&8&10&12&14 \newline \space \newline \text{number of dogs}\space\space&1&2&3&4&5&6&7 \newline \text{number of legs}\space\space&4&8&12&16&20&24&28 \newline \end{array}
1 chicken and 7 dogs have legs
2 chickens and 6 dogs have legs
3 chickens and 5 dogs have legs
4 chickens and 4 dogs have legs
5 chickens and 3 dogs have legs -
A class of 26 boys and 39 girls must be divided into small groups for an activity.
- If the teacher wants equal numbers of boys and girls in each group, what is the maximum number of groups she can form?
Find the largest number that can divide into 26 and 39, that is, the HCF.
The teacher can form 13 groups.
- How many boys and how many girls are in each group?
boys
girls
- After the first activity, the teacher realises that there should be only 2 boys and 2 girls in each group. She decides to form a few groups with only girls. How many additional groups with 4 girls in each can she form?
There are girls to divide into groups.
She can from 3 additional groups.
- Will there be any of the additional groups with more than 4 members?
Yes. One girl is left over, so one group will have 5 members.
2.4 Summary
- A factor is a whole number that divides into a larger number without a remainder. For example, 4 is a factor of 24.
- A prime factor is a factor that is also a prime number. For example, 3 is a prime factor of 24, but 8 is not a prime factor.
- We can express any non-prime number as a product of its prime factors. For example, 24 can be expressed as .
- Index form is a way of writing as a superscript how many times a number is multiplied by itself. For example, means .
- A common factor of two or more numbers is a factor of all the numbers. For example, 4 is a common factor of 8, 24 and 60.
- The highest common factor (HCF) of two or more numbers is the largest factor of all the numbers. For example, 2 is a common factor of 12, 24 and 60, but 4 is the highest common factor of the three numbers.
- A multiple is a whole number into which a smaller number divides without a remainder. For example, 24 is a multiple of 4.
- A common multiple of two or more numbers is a multiple of all the numbers. For example, 24 is a common multiple of the numbers 2, 3, 4 and 6.
- The lowest common multiple (LCM) of two or more numbers is the smallest whole number that is a multiple of all the numbers. For example, 24 is a common multiple of 3, 4 and 6, but 12 is the lowest common multiple of the three numbers.
- When we express two or more numbers as prime factors in index form:
- the HCF is the product of the common prime factors to the lowest index
- the LCM is the product of all the prime factors to the highest index.
