Chapter 10: Trigonometry
There are many different branches of Mathematics. You have worked with algebra and geometry, for example. In this chapter you will be introduced to another branch of Mathematics, namely trigonometry.
The word "trigonometry" comes from two Greek words:
- trigon means triangle
- metria means measurement.
So, trigonometry is the branch of Mathematics in which we study the relationships between the sides and angles of triangles, and their measurements.
trigonometry Trigonometry is the study of the relationships between the sides and angles of triangles.
Trigonometry was developed by Greek mathematicians, so we often use Greek letters when we do trigonometry. Some examples of Greek letters include:
- is the Greek letter "alpha"
- is the Greek letter "beta"
- is the Greek letter "theta"
- is the Greek letter "delta"
10.1 Trigonometric ratios
Before we start to explore the theory of trigonometry, complete the following exercise to get a better understanding of the foundation of trigonometry.
Exercise 10.1: Investigate ratios of similar triangles
-
Consider the three right-angled triangles given below. The triangles are similar, because their matching angles are the same and their matching sides are in proportion.

Use the lengths of the sides indicated to give the ratios of the sides listed below. Give your answers as simplified fractions.
-
What do you notice about your answers in question 1?
The numerical value of the three ratios is the same.
-
Use the lengths of the sides indicated to give the ratios of the sides listed below. Give your answers as simplified fractions.
-
What do you notice about your answers in question 3?
The numerical value of the three ratios is the same.
-
Use the lengths of the sides indicated to give the ratios of the sides listed below. Give your answers as simplified fractions.
-
What do you notice about your answers in question 5?
The numerical value of the three ratios is the same.
-
Use the lengths of the sides indicated to give the ratios of the sides listed below. Give your answers as simplified fractions.
-
What do you notice about your answers in question 7?
The numerical value of the three ratios is the same.
Identifying sides in a right-angled triangle
You will have noticed in the exercise above that if the matching angles are the same, then the ratios of the matching sides will also be the same, even if the lengths of the sides are different.
In Chapter 9, you learnt that we can say that two shapes are similar if their matching sides are in proportion, and their matching angles are equal.
In the right-angled triangles below, is similar to .
In similar triangles, the ratios of the lengths of their corresponding (matching) sides are equal.
Use your fingers to trace over the sides to identify the corresponding sides and the ratios that are equal. If you start at and :
\begin{align} \dfrac{AB}{BC} & = \dfrac{DE}{EF} \\ \dfrac{AC}{BC} & = \dfrac{DF}{EF} \\ \dfrac{AB}{AC} & = \dfrac{DE}{DF} \\ \end {align}The ratios of similar right-angled triangles are used in trigonometry. Specific words are used to name the sides.
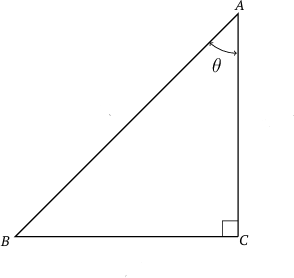
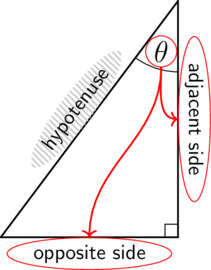
Consider the right-angled triangle below, with marked (we say "theta").
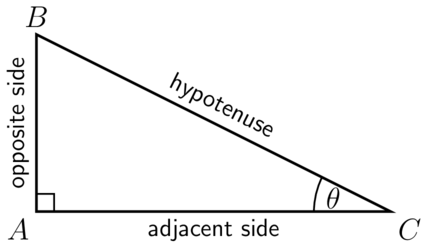
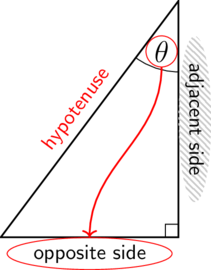
In a right-angled triangle, we refer to the three sides according to how they are placed in relation to the angle .
- The side opposite the right angle is called the hypotenuse. The hypotenuse is always the longest side in the triangle.
- The side opposite is called the opposite side.
- The side next to is called the adjacent side.
If we mark as , then the sides will be named as follows:
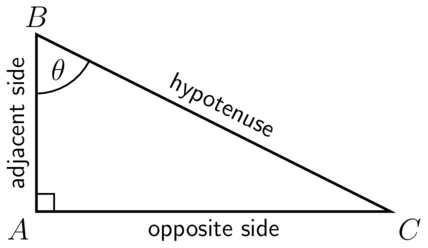
The hypotenuse remains the same no matter which interior angle you are using, because it is always opposite the right angle and it is always the longest side of the triangle. The opposite and adjacent sides depend on the angle from which we are looking.
hypotenuse The hypotenuse is the side opposite the right angle, and is always the longest side of a triangle.
opposite side The opposite side is the side opposite the given angle.
adjacent side The adjacent side is the side next to the given angle.
The definitions of opposite side, adjacent side and hypotenuse can only be used when working with right-angled triangles. Always check to make sure that the triangle has a right angle before you use the definitions, otherwise you will get the wrong answer.
Worked example 10.1: Identifying sides in a right-angled triangle
For the given triangle, label the hypotenuse, opposite side and adjacent side in relation to .
-
Step 1: Identify the hypotenuse.
The hypotenuse is always opposite the right angle.
Hypotenuse:
-
Step 2: Identify the side that is opposite angle .
Side is directly opposite angle .
Opposite side:
-
Step 3: Identify the side that is adjacent to angle .
Side is "attached" to angle .
Adjacent side:

Exercise 10.2: Identify sides in a right-angled triangle
-
For the following triangle, label the hypotenuse, opposite side and adjacent side of the triangle in relation to .

- Hypotenuse:
- Opposite side:
- Adjacent side:

-
The diagram below shows a right-angled triangle with sides labelled Side 1, Side 2 and Side 3. There is an acute angle, angle . Consider the diagram and answer the questions that follow.

- Which side is the hypotenuse?
The hypotenuse is Side 3.
- Which sides are opposite and adjacent to the angle ?
The side opposite angle is Side 2. The side adjacent to angle is Side 1.
-
The diagram below shows a right-angled triangle with sides , and , and two acute angles: , and .

- Which side is opposite angle ?
The side opposite angle is .
- Which side is opposite angle ?
The side opposite angle is .
-
The diagram below shows a right-angled triangle with sides , and , and two acute angles: and .
- Which side is adjacent to angle ?
The side adjacent to angle is .
- Which side is adjacent to angle ?
The side adjacent to angle is .
-
In each of the following five triangles, state whether , and is the hypotenuse, opposite side or adjacent side of the triangle with respect to .
- Triangle 1:
- is the adjacent side
- is the hypotenuse
- is the opposite side
- Triangle 2:
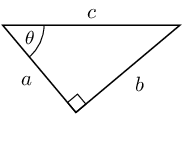
- is the adjacent side
- is the opposite side
- is the hypotenuse
- Triangle 3:
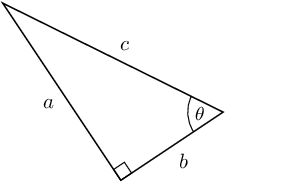
- is the opposite side
- is the adjacent side
- is the hypotenuse
- Triangle 4:
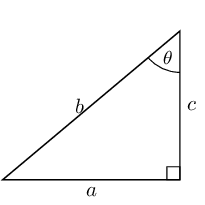
- is the opposite side
- is the hypotenuse
- is the adjacent side
- Triangle 5:
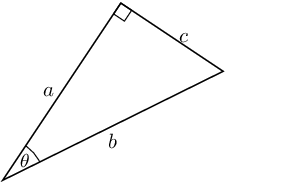
- is the adjacent side
- is the hypotenuse
- is the opposite side
-
The diagram below shows a right-angled triangle with sides labelled Side 1, Side 2 and Side 3. There are two acute angles, angle and angle .
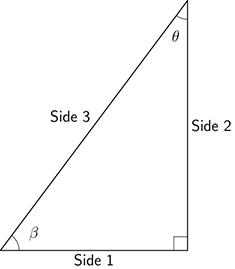
- Which side is the hypotenuse?
The hypotenuse is Side 3.
- Which sides are opposite and adjacent to the angle ?
The side opposite angle is Side 1. The side adjacent to angle is Side 2.
- Which sides are opposite and adjacent to the angle ?
The side opposite angle is Side 2. The side adjacent to angle is Side 1.

-
Explain what is wrong with the following diagram.
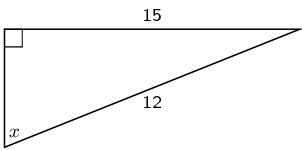
The given lengths are incorrect. The hypotenuse is always the longest side of the right-angled triangle, but in this triangle, the hypotenuse is labelled as being shorter than one of the other sides.
Defining trigonometric ratios in a right-angled triangle
We give special names to the ratios of specific sides in a right-angled triangle. There are three ratios that form the basis of trigonometry.
The names given to the trigonometric ratios are:
- .
These names are abbreviations of the full names, which are:
- is an abbreviation of "the sine of "
- is an abbreviation of "the cosine of "
- is an abbreviation of "the tangent of ".
You cannot do a calculation with or or on its own: sine, cosine and tangent are each a ratio of sides in a right-angled triangle related to a specific angle. So, you always work with the sine of an angle, such as , or the cosine of an angle, such as , or the tangent of an angle, such as .
It will be very helpful for you to memorise these ratios. To help you, just remember this strange word: SOHCAHTOA. It comes from:
SOH:
CAH:
TOA:
Worked example 10.2: Finding trigonometric ratios
Give the ratio for in the following triangle.
-
Step 1: Identify the hypotenuse, opposite side and adjacent side in relation to the angle marked in the given triangle.
- Hypotenuse:
- Opposite side:
- Adjacent side:
-
Step 2: Write down the definition for and substitute the correct sides.
You can use SOHCAHTOA to help you remember the definition for tan. Tan is TOA, so it is opposite side over adjacent side.
\begin{align} \tan\theta& = \dfrac{\text{opposite side}}{\text{adjacent side}} \\ &= \dfrac{BC}{AC} \\ \end{align}
It is important to use the correct notation when you write down a calculation in Mathematics.
- means "point ".
- means "angle ".
- means "the cosine of angle ". (We do not write .)
Exercise 10.3: Find trigonometric ratios
-
Consider the triangle given below and give each of the trigonometric ratios that follow.
Use SOHCAHTOA to help you remember the definitions for the ratios.
-
State whether the following trigonometric ratios have been given correctly.
Definition of the sine ratio:
This trigonometric ratio has not been given correctly.
This trigonometric ratio has been given correctly.
-
Which trigonometric ratio of is defined as the adjacent side over the hypotenuse in the given triangle?

The ratio defined as the adjacent side over the hypotenuse is .
-
Which trigonometric ratio of is defined as the opposite side over the hypotenuse in the given triangle?
The ratio defined as the opposite side over the hypotenuse is .
-
Which trigonometric ratio of is defined as the opposite side over the adjacent side in the given triangle?
The ratio defined as the opposite side over the adjacent side is .
-
Consider the following diagram and answer the questions that follow.
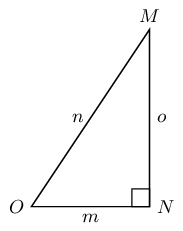
- Write down in terms of , and .
- Write down in terms of , and .
- Write down in terms of , and .
- Write down in terms of , and .
-
State which sides of the triangle you would use to find , and .
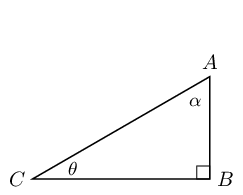
Identify the sides with respect to first:
- hypotenuse =
- opposite side =
- adjacent side =
Therefore:
- =
- =
- =
-
Which of these statements is true about ?
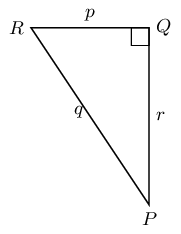
A: =
B: =
C: =
D: =Looking at each of the given ratios we can see that only statement C is correct.
is correct.
-
The triangle below is right-angled at . Use the triangle to answer the questions that follow.
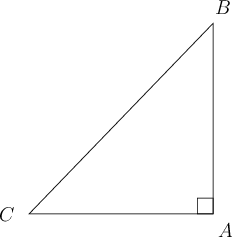
- What is the part of the statement represented by in the following equation?
The missing part of the statement is .
- What is the part of the statement that would make the following equation complete?
The missing part of the statement is .
-
The triangle below is right-angled at . Use the triangle to answer the following questions.

- What is the part of the statement represented by in the following equation?
The missing part of the statement is .
- What is the part of the statement that would make the following equation complete?
The missing part of the statement is .
Evaluating trigonometric ratios
Now that you know how to identify the different trigonometric ratios, you will be able to give values for the ratios. If you are given the lengths of sides or the sizes of angles of right-angled triangles, you can use the definitions to give the correct values of the ratios.
Worked example 10.3: Evaluating trigonometric ratios
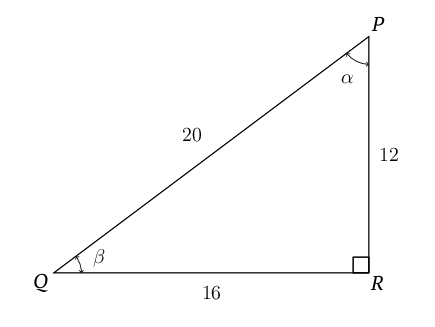
The diagram below shows a right-angled triangle with sides of length 16, 12, and 20 units. The two acute angles are labelled and .
Determine the value of for this triangle. Give your answer as a simplified fraction.
-
Step 1: Write down the definition of the ratio in terms of the sides of this triangle.
Use SOHCAHTOA to help you remember the tan ratio: TOA.
\begin{align} \tan \beta & = \dfrac{PR}{QR} \\ \end{align} -
Step 2: Determine the value of for the given triangle.
It is given that is 12 units in length, and is 16 units. Therefore:
\begin{align} \tan\beta & = \dfrac{PR}{QR} \\ & = \dfrac{12}{16} \\ & = \dfrac{3}{4} \\ \end{align}
Exercise 10.4: Evaluate trigonometric ratios
-
Find the value of the ratio of for the given right-angled triangle.
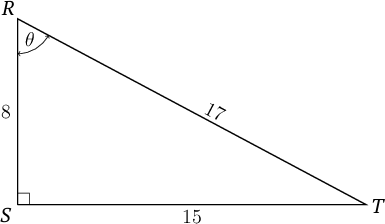
Use SOHCAHTOA to help you remember the sin ratio: SOH.
\begin{align} \sin \theta & = \dfrac{ST}{RT} \\ & = \dfrac{15}{17} \\ \end{align} -
Find the value of the ratio of for the given right-angled triangle.
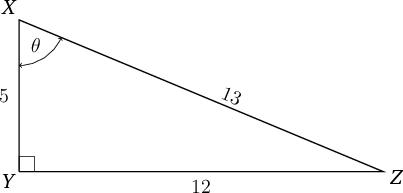
Use SOHCAHTOA to help you remember the cos ratio: CAH.
\begin{align} \cos\theta & = \dfrac{XY}{XZ} \\ & = \dfrac{5}{13} \\ \end{align} -
The diagram below shows a right-angled triangle with sides of length 30, 34, and 16 units. The two acute angles are labelled and .
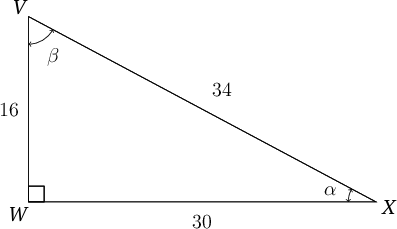
Determine the value of each of the following trigonometric ratios for this triangle.
\begin{align} \sin\beta & = \dfrac{WX}{VX} \\ & = \dfrac{30}{34} \\ & = \dfrac{15}{17} \\ \end{align}
\begin{align} \cos\alpha & = \dfrac{WX}{VX} \\ & = \dfrac{30}{34} \\ & = \dfrac{15}{17} \\ \end{align}
\begin{align} \tan\beta & = \dfrac{WX}{VW} \\ & = \dfrac{30}{16} \\ & = \dfrac{15}{8} \\ \end{align}
\begin{align} \tan\alpha & = \dfrac{VW}{WX} \\ & = \dfrac{16}{30} \\ & = \dfrac{8}{15} \\ \end{align}
-
State which sides of the triangle you would use to find , and . Then find the values of each of the three ratios.
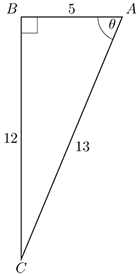
Identify the sides with respect to the angle marked first:
- hypotenuse =
- opposite side =
- adjacent side =
-
Consider the triangle given below. State which statement is correct. Also explain what is incorrect in the other statements.
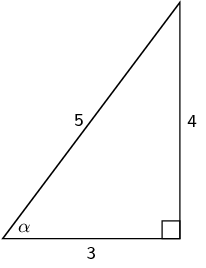
A:
B:
C:
D:A is incorrect, because has the angle and the lengths of the sides switched around.
B is incorrect, because uses the wrong sides with respect to for .
C is correct.
D is incorrect, because uses the wrong sides with respect to for the ratio. Note that you may give the fraction as a decimal number, but first you need to write the correct fraction.
-
The following equation is based on the triangle give below.
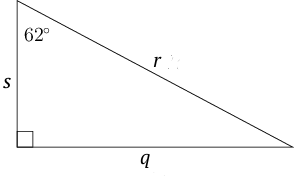
What is the quantity represented by ?
The missing quantity is .
-
Use the triangle below to find the following ratios.
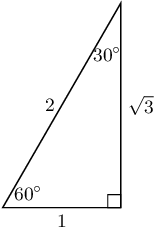
Leave your answers in surd (root) form where necessary.
-
Use the triangle below to find the following ratios.
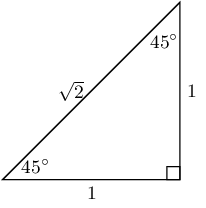
Leave your answers in surd form where necessary.
-
The diagram below shows a right-angled triangle, with acute angles labelled and . The sides of the triangle are labelled 6, 8 and 10 units. Answer the questions that follow. Give fractions in their simplest form.
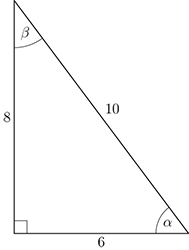
- Write down the value of .
\begin{align} \sin \alpha & = \dfrac{8}{10} \\ & = \dfrac{4}{5} \end{align}
- Write down the value of .
\begin{align} \cos \beta & = \dfrac{8}{10} \\ & = \dfrac{4}{5} \end{align}
- What do you notice about the two answers above?
The two answers are the same, so .
In question 9 in the exercise above, because of the following rule.
In a right-angled triangle, the two angles other than the right angle will always add up . So in the triangle in question 9, + = . The name for two angles that add up to is complementary angles.
In a right-angled triangle, if the two complementary angles are and , then it is always true that:
This is true because the side opposite is the side adjacent to .
10.2 Using trigonometric ratios in calculations
When we know how to identify trigonometric ratios in right-angled triangles, we can use them to calculate unknown sides or angles.
In the exercise above, you have found the trigonometric ratios for some angles, for example, , and . These are always the ratios for these angle sizes. So is always equal to 1.
If we look at , we can work out the numerical value of that ratio, using a calculator:
If you have a scientific calculator, you can work out the numerical value of the trigonometric ratio for any angle size.
If you are given the numerical value of a specific ratio, you can work out the size of the angle. For example, if you were given , then you could work out that .
You will learn how to do these two types of calculations in the next two worked examples.
You will need to use a calculator to do these calculations. There are many different kinds of scientific calculators, and some work differently from others. It is important that you know how to use your calculator. Some of the buttons mentioned in this chapter may be different on your calculator.
Make sure that your calculator is set to work in degrees, because we are working with angle sizes in degrees.
- If there is a button marked on your calculator, press on that button.
- If there is a button marked , press this button until for "degrees" displays at the top of the calculator screen.
- The on this button is for "radians" and the is for "gradians". These options are given because angles can also be measured in radians and gradians. You will not need to use them in your calculations for now.
You can also find many calculators online (on the internet) or as apps on cell phones. If you use an online scientific calculator, you can follow the methods described in this chapter. There are also online calculators available that only do trigonometric calculations, but it is best to use a scientific calculator for your work in this chapter.
When working with trigonometric ratios, if no instructions are given, round off your answers to two decimal places. Make sure that you only round off in the final step. If you round off too soon, your final answer may not be accurate.
Worked example 10.4: Finding the value of a ratio if the angle size is given
Use a calculator to determine the value of .
-
Step 1: Make sure you know what you need to work out.
You are given the size of an angle, .
You have been asked to calculate the numerical value of the sine of that angle size.
-
Step 2: Enter each part of the calculation on your calculator in the correct order.
Work from left to right:
-
Step 3: Read off the answer.
The calculator should give the following: 0.9520…
-
Step 4: Round off the answer and write it down.
If no instructions are given, round off to two decimal places. Do not include any units the answer.
When you are given the angle size, and you need to find a numerical value for a particular ratio of that angle, as in the worked example above, you are simplifying (or evaluating) an expression.
An expression that contains a trigonometric ratio can also involve other operations, such as multiplication or division. In the worked example below, you will learn how to use a calculator to multiply a trigonometric ratio.
Worked example 10.5: Multiplying the value of a ratio for a given angle size
Use a calculator to determine the value of .
-
Step 1: Make sure you know what you need to work out.
You are given the size of an angle, .
You have been asked to calculate the numerical value of the tan of that angle size, and then multiply that value by 3.67.
-
Step 2: Enter each part of the calculation on your calculator in the correct order.
Work from left to right:
-
Step 3: Read off the answer.
The calculator should give the following: 3.61911….
-
Step 4: Round off the answer and write it down.
If no instructions are given, round off to two decimal places. Do not include any units the answer.
As you have seen in the worked example above, if the size of the angle is given, you use one of the following buttons on your calculator to find the numerical value of of a ratio:
, or
If the numerical value of a ratio is given, and you need to find the size of the angle (for example, the value of ), then you need to use one of the following buttons on your calculator to find the angle:
, or
Sometimes these buttons are available next to the , and buttons. If they are not, to get to them, you will need to press a "second function" key on your calculator. This has different names on different calculators, such as:
, or , or , or , or
Make sure the scientific calculator you are using has one of these buttons, and that you can get to the , and buttons.
To get, for example, from to on an actual scientific calculator, you will need to:
- press the "second function" key, such as or
- then press
- and this should activate on your calculator.
On online calculators, sometimes if you press one of these keys or buttons, you are taken to a different screen that has the options.
If you are not sure how to get to the options on your calculator, ask for advice.
Worked example 10.6: Finding the the angle size if the value of a ratio is given
Use a calculator to solve for if .
-
Step 1: Make sure you know what you need to work out.
You are given the numerical value of the cosine of an angle, .
You are not given , so you need to calculate what the size of the angle is.
-
Step 2: Enter each part of the calculation on your calculator in the correct order.
You will need to press a "second function" key on your calculator to get to . Press that key first, and then:
-
Step 3: Read off the answer.
The calculator should give the following: 68.34604…
-
Step 4: Round off the answer and write it down.
If no instructions are given, round off to two decimal places.
is an angle, and it is important to show that the angle is measured in degrees by writing the after your answer.
\begin {align} \cos \theta & = 0.369\\ \therefore \theta & = \cos^{-1} 0.369 \\ & = 68.3460... \\ \end {align}=
You will have noticed in the worked example above that when you need to find the size of an angle, you are solving an equation. You needed to solve for .
Exercise 10.5: Use a calculator in trigonometry
-
Use a calculator to find the values of each of the following expressions. Round your answers to two decimal places.
Take note that sometimes you need to press and then to calculate the value of the ratio first. Only then can you divide by 0.5.
-
Use a calculator to find the value of the unknown angle in each case. Show how you solve the equation, and round your answer to two decimal places.
\begin {align} \sin \theta & = 0.572\\ \therefore \theta &= \sin^{-1} 0.572 \\ &= 34.8898... \\ \end {align}
=
\begin {align} \cos \alpha & = 0.181\\ \therefore \alpha &= \cos^{-1} 0.181 \\ &= 79.57^{\circ} \\ \end {align}
\begin {align} \tan \beta & = 2.53\\ \therefore \beta &= \tan^{-1} 2.53 \\ &= 68.43^{\circ} \\ \end {align}
\begin {align} \sin \theta &= \dfrac{2}{7} \\ \therefore \theta & = \sin^{-1} \left( \frac{2}{7} \right) \\ &= 16.60^{\circ} \\ \end {align}
\begin {align} \cos \alpha & = \dfrac{5}{11} \\ \therefore \alpha & = \cos^{-1} \left( \frac{5}{11} \right) \\ & = 62.96^{\circ} \\ \end {align}
\begin {align} \tan \delta & = \dfrac{14}{5} \\ \therefore \delta & = \tan^{-1} \left( \frac{14}{5} \right ) \\ & = 70.35^{\circ} \\ \end{align}
If you are given the sizes of two sides or two angles of a triangle, you can calculate the sizes of the other sides and angles. Now that you are familiar with your calculator, you are ready to calculate unknown sides or angles in right-angled triangles. In all these calculations the most important part of the solution will be to decide which one of the three trigonometric ratios to use.
To help you to identify which trigonometric ratio you should use, you can use colours and shading to show the angle(s) and side(s) that are given, as well as the angle or side that you have to calculate.
Once you have two sides and an angle in colour, you will find it easier to decide which ratio to use.
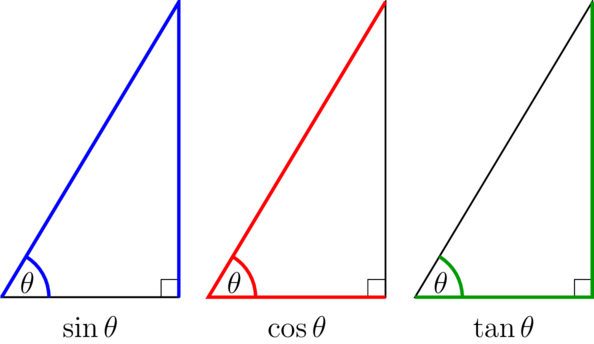
- Use if an angle, its opposite side and the hypotenuse are given (in blue).
- Use if an angle, its adjacent side and the hypotenuse are given (in red).
- Use if an angle, its opposite side and its adjacent side are given (in green).
Worked example 10.7: Identifying the correct trigonometric ratio to calculate a missing side
Study the given right-angled with . The angle given in the diagram is . The side given is .
Calculate the length of side . Round your answer to two decimal places if appropriate.
-
Step 1: Use colour to mark the given side and angle, as well as the angle that you have to calculate.
If you can, rotate the triangle so that it is easy to recognise the ratio.
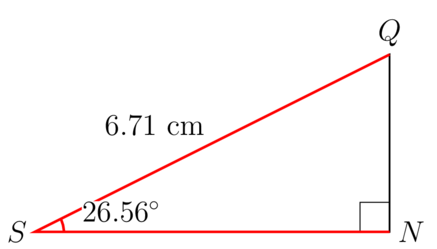
-
Step 2: Decide which trigonometric ratio to use and write down the definition.
You are given a side that is adjacent to the angle and the hypotenuse.
Use SOHCAHTOA to help you remember the ratios. "CAH" includes adjacent and hypotenuse, so the ratio you need to use is the cosine of the angle.
\begin{align} \cos S & = \dfrac{\text {adjacent}}{\text {hypotenuse}} \\ \end{align} -
Step 3: Write the ratio in terms of its sides, and substitute the given values into the equation.
\begin{align} \cos S & = \dfrac{SN}{SQ} \\ \cos 26.56^{\circ} & = \dfrac{SN}{6.71} \\ \end{align} -
Step 4: Solve the equation.
Write the ratio on the left hand side as a fraction with a denominator of 1.
Then you have one fraction equal to another fraction, and you can multiply both sides of the equation by the multiplicative inverse.
\begin{align} \dfrac{\cos 26.56^{\circ}}{1} & = \dfrac{SN}{6.71} \\ \dfrac{6.71}{1} \times \dfrac{\cos 26.56^{\circ}}{1} & = \dfrac{SN}{6.71} \times \dfrac{6.71}{1}\\ 6.71 \times \cos 26.56^{\circ} &= SN\\ \end{align} -
Step 5: Use a calculator to work out the answer.
\begin{align} SN & = 6.71 \cos 26.56^{\circ} \\ & = 6.00187... \\ \end{align} -
Step 6: Give the answer in full and rounded off correctly.
The length of is .
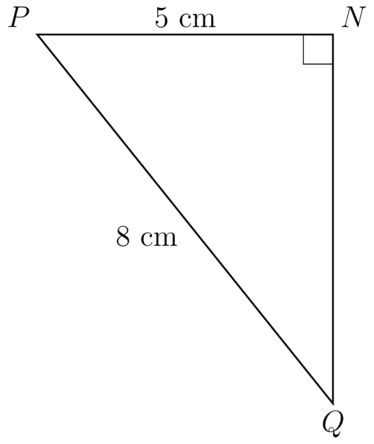
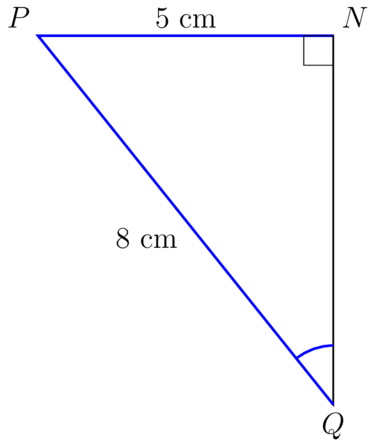
Worked example 10.8: Identifying the correct trigonometric ratio to calculate a missing angle
The diagram below shows right-angled with . The sides given are = and = .
Calculate the value of . Round your answer to two decimal places if appropriate.
-
Step 1: Use colour to mark the given sides as well as the unknown angle.
-
Step 2: Decide which trigonometric ratio to use and write down the definition.
Side is opposite the unknown angle.
Side is the hypotenuse.
The trigonometric ratio linking the opposite side to the hypotenuse is the sine ratio.
\begin{align} \sin Q & = \dfrac{NP}{PQ} \\ \end{align} -
Step 3: Substitute the given values.
\begin{align} \sin Q & = \dfrac{NP}{PQ} \\ & = \dfrac{5}{8} \\ \end{align} -
Step 4: Solve the equation.
\begin{align} \sin Q & = \dfrac{NP}{PQ} \\ & = \dfrac{5}{8} \\ \therefore \hat {Q} & = \sin^{- 1} \left( \frac{5}{8} \right) \\ & = 38.68218... \\ \end{align} -
Step 5: Give the answer in full, rounded off correctly, and including the degree symbol.
=
Exercise 10.6: Use the correct trigonometric ratios to calculate missing sides and angles
-
Study the given right-angled with . The sides given are = and = .
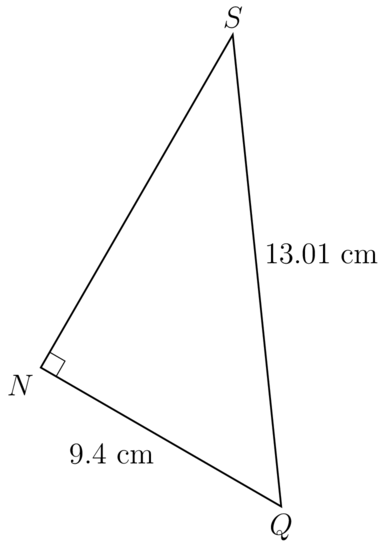
Calculate the value of . Round your answer to two decimal places if appropriate.
Find the correct trigonometric ratio to solve for the unknown angle.
\begin{align} \sin S & = \dfrac{NQ}{SQ} \\ & = \dfrac{9.4}{13.01} \\ \therefore \hat {S} & = \sin^{- 1} \left( \frac{9.4}{13.01} \right) \\ & = 46.26302... \\ \end{align} The coloured lines and angle correspond to the sine ratio, opposite over hypotenuse.
The coloured lines and angle correspond to the sine ratio, opposite over hypotenuse.=
-
Determine the value of in the diagram given below.
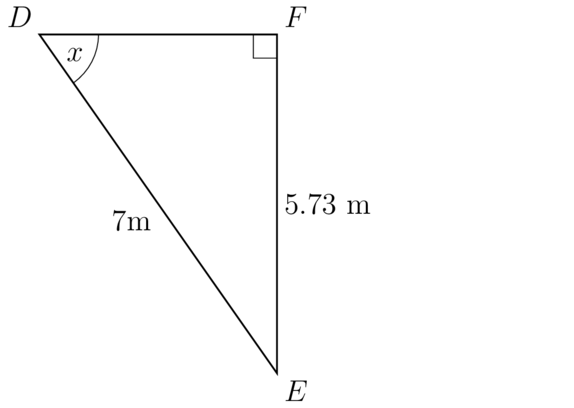
\begin{align} \sin x & = \dfrac{FE}{DE} \\ & = \dfrac{5.73}{7} \\ \therefore x & = \sin^{- 1}\left( \frac{5.73}{7} \right) \\ & = 54.9420... \\ \end{align}
-
Determine the value of in the given triangle.
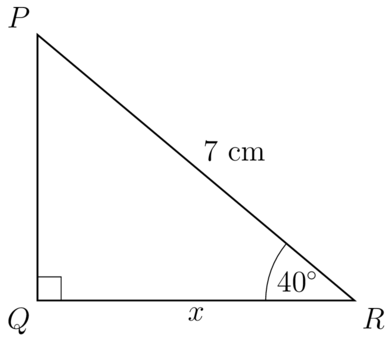
\begin{align} \cos R & = \dfrac{QR}{PR} \\ \cos \text{40}^{\circ} & = \dfrac{x}{7} \\ \dfrac{\cos \text{40}^{\circ} }{1} & = \dfrac{x}{7} \\ x & = 7 \cos \text{40}^{\circ} \\ & = 5.36231... \\ \end{align}
=
-
Determine the value of in the triangle given below.

\begin{align} \cos \theta & = \dfrac{BC}{AC} \\ & = \dfrac{8.19}{10} \\ \therefore x & = \cos^{-1} \left( \frac{8.19}{10} \right) \\ & = 35.0151... \\ \end{align}
=
-
Determine the value of in the given triangle. Give the answer rounded off to one decimal place.
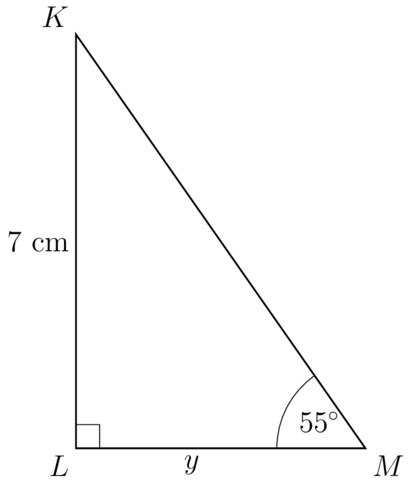
\begin{align} \tan M & = \dfrac{KL}{LM} \\ \tan \text{55}^{\circ} & = \dfrac{7}{y} \\ \dfrac {\tan \text{55}^{\circ} } {1} & = \dfrac{7}{y} \\ y \times \tan \text{55}^{\circ} & = 7 \\ y \times \tan \text{55}^{\circ} \div {\tan \text{55}^{\circ}} & = 7 \div {\tan \text{55}^{\circ}} \\ y & = 4.9014... \\ \end{align}
=
-
Determine the value of in the triangle given below.
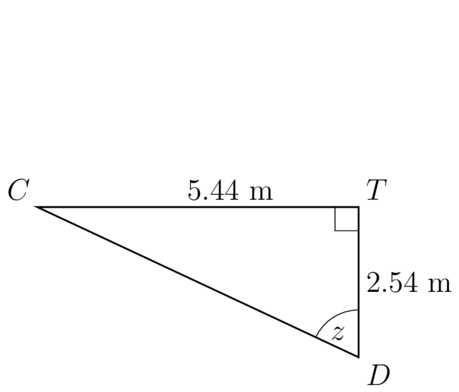
\begin{align} \tan z & = \dfrac{CT}{DT} \\ & = \dfrac{5.44}{2.54} \\ \therefore z & = \tan^ {-1} \left( \frac{5.44}{2.54}\right) \\ & = 64.9715... \\ \end{align}
=
10.3 Practical applications
It is very useful to know how to use trigonometric ratios to calculate an unknown side or an unknown angle in a right-angled triangle. There are often real-life situations that we can represent using a right-angled triangle. Then we use the trigonometric ratios to calculate unknown values.
Worked example 10.9: Using trigonometry to solve problems
A person stands at point , looking up at a bird sitting at the top of a tree at point .
The height of the tree is metres, point is metres away from the foot of the tree, and the angle of inclination (upwards from the horizontal) to the top of the tree is .
Calculate the height of the tree ( ) as shown in the diagram below. Round your answer to two decimal places if necessary.
-
Step 1: Decide which trigonometric ratio to use. Write down the definition of the ratio in terms of the lines.
In relation to , the side that you need to calculate is , which is opposite, and , which is adjacent. If we have opposite and adjacent sides, we need to use tan.
\begin{array}{ll} \tan A & = \dfrac{BC}{AC} \\ \end{array} -
Step 2: Substitute the given values.
\begin{align} \tan A &= \dfrac{BC}{AC} \\ \tan 35^{\circ} &= \dfrac{x}{7.14} \\ \end{align} -
Step 3: Multiply across and solve for .
\begin{align} \dfrac {\tan 35^{\circ} }{1} &= \dfrac{x}{7.14} \\ x & = \text{7.14} \times \tan 35^{\circ} \\ x & = \text{4.9994...} \\ \end{align} -
Step 4: Round the answer off to two decimal places and remember to include the correct units.
The height of the tree, , is .
Exercise 10.7: Use trigonometry to solve problems
-
A person stands at point , looking up at a satellite dish on the top of a building, at point .
The height of the building is , the line-of-sight distance from point to the top of the building (point ) is , and the angle of inclination (from the horizontal) to the top of the building is .
Calculate the line-of-sight distance to the top of the building ( ). Round your answer to one decimal place.

Because you have opposite over hypotenuse, use the sine ratio to solve for .
\begin{align} \sin A & = \dfrac{BC}{AB} \\ \sin 62^{\circ} & = \dfrac{6}{x} \\ \dfrac {\sin 62^{\circ} }{1} & = \dfrac{6}{x} \\ x \times \sin 62^{\circ} &= 6 \\ x & = 6 \div {\sin 62^{\circ} } \\ & = 6.79542... \\ \end{align}The line-of-sight distance to the top of the building is .
-
Ayanti is outside flying a kite. Here are two facts about the situation:
- The distance straight from Ayanti to the kite is .
- The height of the kite above the ground is .
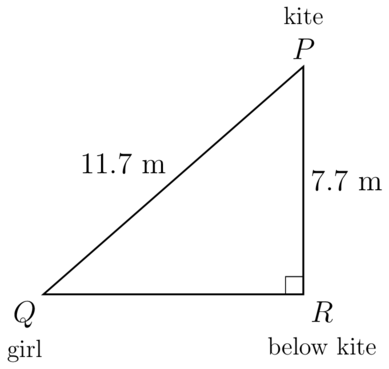
Calculate the angle of inclination from Ayanti up to the kite.
Round your answer to two decimal places.
You need to solve for the size of the angle at . Use the sine ratio to solve for .
\begin{align} \sin Q & = \dfrac{PR}{PQ} \\ & = \dfrac{7.7}{11.7} \\ \therefore Q & = \sin^{- 1}\left( \frac{7.7}{11.7} \right) \\ & = \text{41.1566...} \\ \end{align}The angle of inclination from Ayanti up to the kite is .
-
A person stands at point , looking up at a bird sitting on the top of a tree, point .
Point is metres away from the foot of the tree, the line-of-sight distance from point to the top of the tree (point ) is metres, and the angle of inclination (from the horizontal) to the top of the tree is .
Calculate the distance between the person and the foot of the tree ( ), as shown in the diagram. Round your answer to one decimal place.

Use the cosine ratio to solve for .
\begin{align} \cos L & = \dfrac{JL}{KL} \\ \cos 65^{\circ} & = \dfrac{x}{9.93} \\ \dfrac{\cos 65^{\circ}} {1} & = \dfrac{x}{9.93} \\ \therefore x & =9.93 \times \cos 65^{\circ}\\ & = 4.1965... \\ \end{align}The distance between the person and the foot of the tree, , is 4.2 m.
-
A person sits at point , looking up at the top of a tree, point .
Point is metres away from the foot of the tree, the line-of-sight distance from point to the top of the tree is metres, and the angle of inclination from the horizontal to the the top of the tree is .
Calculate the angle of inclination, . Round your answer to two decimal places.

Use the cosine ratio to solve for .
In this case, you need to calculate the cos ratio of one value divided by another value. You can do this in one step on your calculator without pressing in between.
\begin{align} \cos\beta & = \dfrac{QR}{PR} \\ & = \dfrac{5.03}{7.83} \\ \therefore \beta & = \cos^{-1} \left(\frac{5.03}{7.83} \right) \\ \therefore \beta & = 50.0289... \\ \end{align}The angle of inclination from the horizontal to the the top of the tree, , is .
-
Akeju made a scale drawing of a wooden construction that she noticed next to a lake. On her scale drawing, = and = . Calculate the length of on the scale drawing. Round the answer off to one decimal place.

Use the tangent ratio to find .
\begin{align} \tan A & = \dfrac{BC}{AB} \\ \tan 53^{\circ} & = \dfrac{BC}{3} \\ \dfrac{\tan 53^{\circ}} {1} & = \dfrac{BC}{3} \\ \therefore BC & = 3 \times \tan 53^{\circ} \\ & = 3.9811... \\ \end{align}=
-
A man is sitting in a small boat, fishing on a lake. He catches a fish. The horizontal distance from the man in the boat to the point directly above the fish is . The distance from the surface of the water straight down to the fish is .
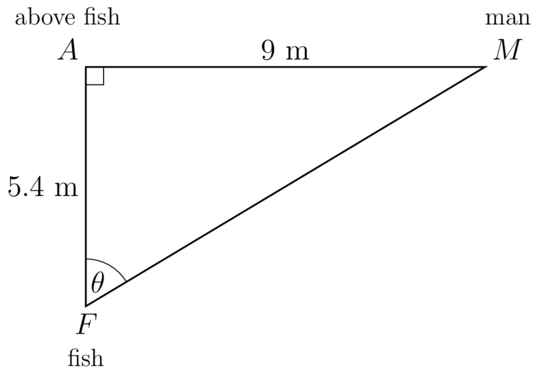
Find the angle at the fish's position between the man and the vertical direction.
Round your answer to two decimal places.
Use tan to solve for .
\begin{align} \tan F & = \dfrac{AM}{AF} \\ & = \dfrac{9}{5.4} \\ \therefore \theta & = \tan^{- 1}\left( \frac{9}{5.4} \right) \\ & = \text{59.0362...} \\ \end{align}=
-
is a flagpole on top of a building. The width of the building is and the line-of-sight ( ) from the top of the building to the top of the flagpole is .

Answer the following two questions and round your answers off to two decimal places.
- Calculate the size of .
Use the sine ratio to solve for .
\begin {align} \sin P &= \dfrac{QR}{PR} \\ & = \dfrac{5}{5.32} \\ \therefore \hat {P} & = \sin^{-1} \left( \frac{5}{5.32} \right) \\ & = 70.0263...\\ \end {align}=
- Calculate the height of the flagpole.
Use the Theorem of Pythagoras to calculate the length of .
\begin{align} {PQ}^{2} + {QR}^{2} &= {PR}^{2} \quad (\text{Pythagoras}) \\ {PQ}^{2} + 5^{2} & = {5.32^{2}} \\ {PQ}^{2} + 25 - 25 & = 28.3024 - 25 \\ {PQ}^{2} & = 3.3024\\ \therefore PQ & = \sqrt {3.3024} \\ & = 1.81725... \\ \end{align}The height of the flagpole is .
-
An architect designed a house, but she did not have time to fill in all the measurements on the diagram. The architect said that = and = . The front view of the house shows an isosceles triangle on top of a rectangle.
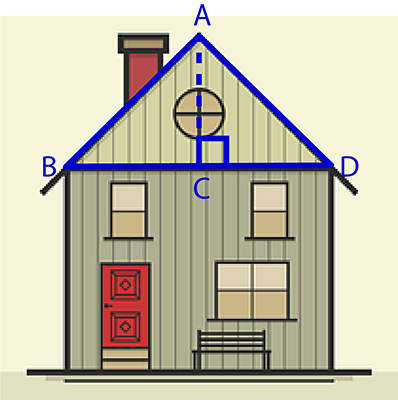
Use the diagram to carry out the following calculations. Round your answer to two decimal places.
- Calculate the size of .
Calculate the length of in isosceles :
\begin {align} CD & = BD \times \dfrac{1}{2} \\ & = \text{9 m} \times \dfrac{1}{2} \\ & = \text{4.5 m} \\ \end {align}Use the tangent ratio to solve for :
In :
\begin {align} \tan D & = \dfrac{AC}{CD} \\ & = \dfrac{3.8}{4.5} \\ \therefore \hat {D} & = \tan^{-1} \left( \frac{3.8}{4.5} \right) \\ & = 40.17923... \end {align}=
- Calculate the length of .
Use the Theorem of Pythagoras to calculate the length of .
\begin{align} AD^{2} & = AC^{2} + CD^{2} \quad (\text{Pythagoras}) \\ & = 3.8^{2} + 4.5^{2} \\ & = 14.44 + 20.25 \\ & = 34.69 \\ \therefore AD & = \sqrt {34.69} \\ & = 5.88982... \\ \end{align}=
10.3 Summary
- Trigonometry is the study of the relationships between the sides and angles of triangles.
- In a right-angled triangle, we refer to the three sides according to how they are placed in relation to the
angle ðœƒ.
- The side opposite the right angle is called the hypotenuse. The hypotenuse is always the longest side in the triangle.
- The side opposite is called the opposite side.
- The side next to is called the adjacent side.
- We define three trigonometric ratios for right-angled triangles:
- We use trigonometric ratios in right-angled triangles to calculate missing lengths of sides or sizes of angles.
- We often use calculators when we do these calculations.
- We can represent real life situations using a right-angled triangle and then use trigonometric ratios to calculate unknown values.