Chapter 4: Equivalent fractions
4.1 Types of fractions
A fraction is part of a whole. There are different ways to write fractions. One way is to write the fraction as one whole number on top of another whole number with a dividing line between, as .
The bottom number is called the denominator. It represents all the parts that the whole is divided into. The top number is called the numerator. It represents only the parts of the whole we are dealing with. Fractions that are written like this are called common fractions.
fraction A fraction is a part of a whole.
denominator The denominator is the number written below the line in a fraction; it represents all the parts of a whole.
numerator The numerator is the number written above the line in a fraction; it represents only the parts of a whole we are dealing with.
common fraction A common fraction is a fraction that is written in the form , where the numerator and denominator are both whole numbers.
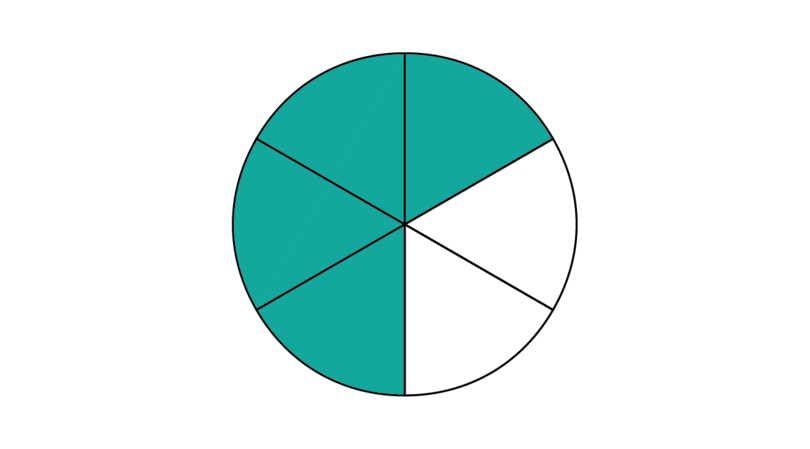
For example, if you cut a cake into seven pieces, you can say that the whole cake is made up of .
Suppose you eat two of the pieces.
- The fraction of the cake you ate is . The denominator shows that the cake was cut into 7 pieces. The numerator shows that 2 pieces were eaten.
- The fraction of the cake that is left over is . The denominator still shows that the cake was cut into 7 pieces. The numerator now shows that 5 pieces are left over.
The fractions and are proper fractions. A proper fraction is smaller than 1. Its numerator is smaller than its denominator.
proper fraction A proper fraction is a fraction that is smaller than 1, so the numerator is smaller than the denominator.
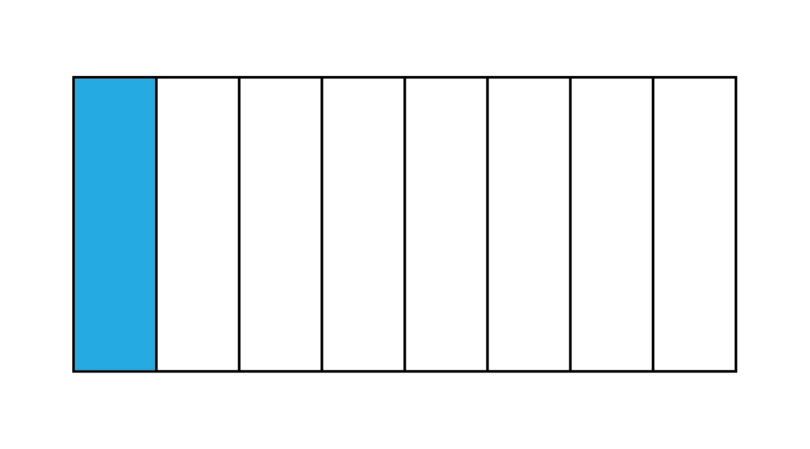
Exercise 4.1: Write proper fractions from diagrams
For each diagram, express the shaded part as a proper fraction.
A mixed number is made up of a whole number and a proper fraction. For example, apples mean you have two whole apples and one half of another apple.
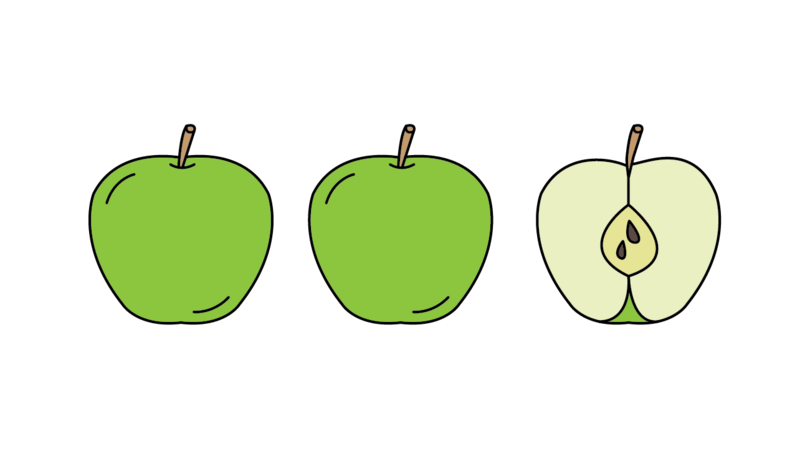
mixed number A mixed number is a number that is made up of a whole number and a proper fraction.
A mixed number may be expressed as an improper fraction. An improper fraction is larger than 1. Its numerator is larger than its denominator. Suppose we cut the two whole apples shown above into halves as well. We will then have five halves.
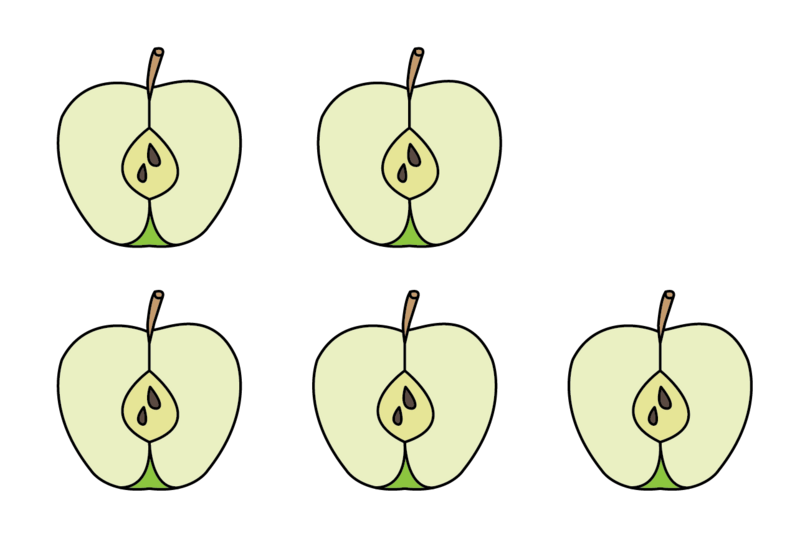
These five halves may be written as . The denominator tells us that there are 2 parts in one whole apple, so we are dealing with halves. The numerator tells us that we have 5 halves. Therefore, the mixed number may be expressed as the improper fraction .
improper fraction An improper fraction is a fraction that is larger than 1, so the numerator is larger than the denominator.
Worked example 4.1: Expressing mixed numbers as improper fractions
Write as an improper fraction.
-
Step 1: Use the denominator to see how many parts there are in one whole.
- The denominator of the proper fraction in this mixed number is 4.
- This means that each whole is divided into 4 parts. We are dealing with quarters.
-
Step 2: Determine how may parts the whole number represents. Multiply the whole number by the denominator from Step 1.
- The whole number in this mixed number is 5.
- If there are 4 parts in one whole, there must be parts in five wholes.
-
Step 3: Add the additional parts that are given by the numerator of the proper fraction.
- The numerator of the proper fraction is 3.
- So, as well as the 20 parts given by the whole number, we have another 3 parts.
- The total parts are .
-
Step 4: Write the improper fraction in the form .
- The numerator gives the total parts we have: 23
- The denominator tells us how many parts there are in one whole: 4
Worked example 4.2: Expressing improper fractions as mixed numbers
Write as a mixed number.
-
Step 1: Use the denominator to see how many parts there are in one whole.
- The denominator of this improper fraction is 3.
- This means that each whole is divided into 3 parts. We are dealing with thirds.
-
Step 2: Determine how many whole numbers can be formed from the total parts we have. To do this, divide the numerator by the denominator from Step 1.
- The numerator gives the total parts we have: 26
- If there are 3 parts in one whole, we can form 8 wholes from 26 parts:
The whole number part of the mixed number is: 8
-
Step 3: Determine what fraction is left over after we formed the whole numbers.
- You know that the denominator, which tells us how many parts there are in one whole, is 3.
- To work out the numerator, use the parts that are left over after we formed the whole numbers. If you look at the long division, the remainder is 2.
After we formed the whole numbers, the fraction is left over.
-
Step 4: Write down the mixed number as a whole number followed by a proper fraction.
Exercise 4.2: Convert between mixed numbers and improper fractions
- Express the following mixed numbers as improper fractions.
Parts in one whole: 7
Parts in 6 wholes:
Total parts:Parts in one whole: 11
Parts in 2 wholes:
Total parts:Parts in one whole: 3
Parts in 13 wholes:
Total parts: - Express the following improper fractions as mixed numbers.
Parts in one whole: 7
Total parts: 30Whole number: 4
Fraction:Parts in one whole: 9
Total parts: 112Whole number: 12
Fraction:Parts in one whole: 11
Total parts: 85Whole number: 7
Fraction:
Once you understand how to express a mixed number as an improper fraction, you may use this short method.
Example:
Denominator:
Numerator:
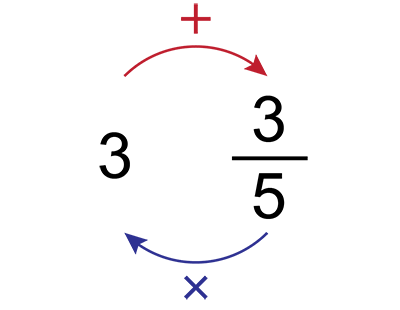
Answer:
4.2 Equivalent fractions
Fractions that represent the same part of a whole in different ways are called equivalent fractions. Look at the three diagrams below. The fraction of the rectangle that is shaded is given next to each diagram.

All three fractions represent half of the rectangle. The fractions have different numerators and denominators, but they all represent the value .
equivalent fractions Equivalent fractions are fractions that have different numerators and denominators, but they represent the same part of a whole, and they have the same value.
Find equivalent fractions
We find equivalent fractions by multiplying or dividing the numerator and the denominator by the same whole number.
Worked example 4.3: Working out equivalent fractions
Find the missing numbers in these equivalent fractions:
-
Step 1: Start with the first pair. Identify what is given, which in this case is the two denominators. Was the first denominator multiplied or divided to get the second denominator, and by what whole number?
The denominator was multiplied by 4 to get 16:
-
Step 2: Repeat the action identified in Step 1 for the remaining part of the fraction.
The numerator must also be multiplied by 4:
-
Step 3: Repeat Steps 1 and 2 to find the next missing number.
The numerator was divided by 2:
The denominator must also be divided by 2:
-
Step 4: Repeat Steps 1 and 2 for the last fraction. If it is not possible to perform Step 1 with the fraction to the left of the missing number, use any other fraction that is complete.
It is not possible to multiply the numerator 6 or the numerator 12 by a whole number and then get 15 as an answer. You have to use the fraction .
The numerator was multiplied by 5:
The denominator must also be multiplied by 5:
-
Step 5: Write down the full answer.
Improper fractions can also have equivalent fractions. Earlier on in this chapter, we showed that apples is equal to apples. The improper fraction tells us that we are dealing with apple halves and that we have 5 apple halves.

Suppose we cut each apple half into two pieces. We will then have ten apple quarters.
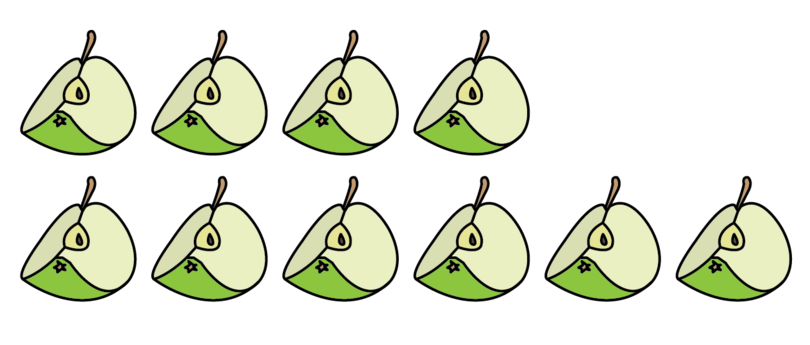
This may be expressed as . The denominator tells us that there are 4 parts in one whole apple, so we are dealing with quarters. The numerator tells us that we have 10 quarters. Therefore, the fractions and are equivalent fractions. In this case, the numerator and denominator were multiplied by 2:
Exercise 4.3: Determine equivalent fractions
Find the missing numbers in each list of equivalent fractions.
Simplify equivalent fractions
A fraction is in its simplest form when the numerator and the denominator have no common factor. For example, is the simplest form of the fractions and . These fractions are not in their simplest form, because in , 2 and 4 have 2 as a common factor, and in , 4 and 8 have 2 and 4 as common factors.
simplest form A fraction is in its simplest form when the numerator and denominator have no common factor.
Worked example 4.4: Finding the simplest form of a fraction
Find the simplest form of the fraction .
-
Method 1 (Prime numbers)
1. Find the smallest prime number that is a factor of both the numerator and the denominator. In this case the factor is 2.
2. Divide both the numerator and denominator by this prime number. Write down the equivalent fraction.
3. Repeat until the prime number can no longer divide into both the numerator and the denominator.
4. Move on to the next prime number that is a factor of both the numerator and the denominator. In this case the factor is 5. Divide both the numerator and the denominator by 5.
5. Repeat this process until the numerator and the denominator have no more common factors.The simplest form of is .
-
Method 2 (HCF)
1. Express both the numerator and the denominator as a product of their prime numbers.
\begin{array}{r | r} 2 & 40 \newline \hline 2 & 20 \newline \hline 2 & 10 \newline \hline 5 & 5 \newline \hline & 1 \end{array} \begin{array}{r | r} 2 & 60 \newline \hline 2 & 30 \newline \hline 3 & 15 \newline \hline 5 & 5 \newline \hline & 1 \end{array}
2. Find the HCF of the numerator and the denominator.
3. Divide the numerator and the denominator by their HCF.The simplest form of is .
If necessary, go back to Chapter 2 to see how to find the highest common factor (HCF) of two or more numbers.
-
Method 3 (Inspection)
1. Find any common factor of the numerator and the denominator.
2. Divide both the numerator and denominator by this factor. Write down the equivalent fraction.
3. Repeat this process until the numerator and the denominator have no more common factors.The simplest form of is .
Exercise 4.4: Simplify fractions
Find the simplest form of each of the following fractions, using the method of your choice.
-
Using Method 1 (Prime numbers):
The simplest form of is .
-
Using Method 1 (Prime numbers):
The simplest form of is .
-
Using Method 2 (HCF):
The simplest form of is .
-
Using Method 2 (HCF):
The simplest form of is .
-
Using Method 3 (Inspection):
The simplest form of is .
Identify equivalent fractions
Fractions that are equivalent have the same simplest form. Look at the two diagrams below. The fraction of the rectangle that is shaded is given next to each diagram.
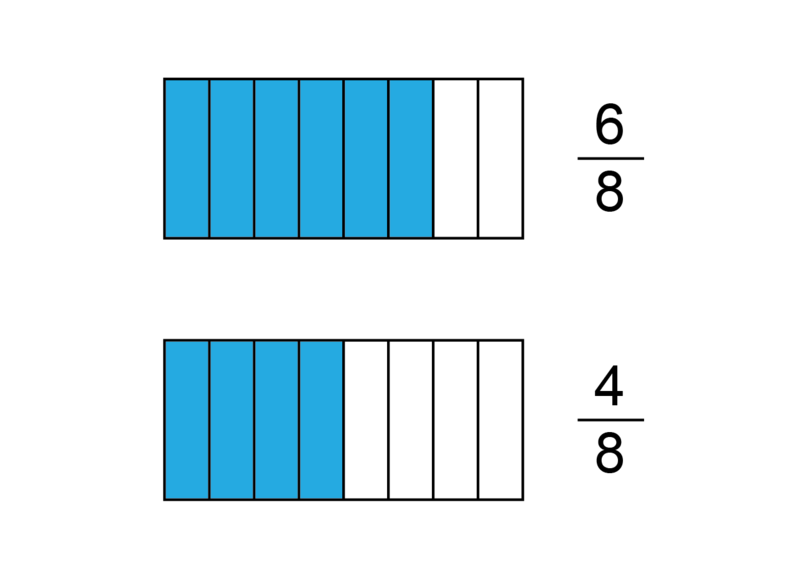
It is easy to see that the fractions and are not equivalent. They do not represent the same part of the whole rectangle. We can check this by finding the simplest form of each fraction.
This shows that the fractions and do not have the same value. They are therefore not equivalent.
Remember that equivalent fractions have the same simplest form.
Exercise 4.5: Determine whether fractions are equivalent or not
For each of the following pairs of fractions, determine whether they are equivalent or not.
-
and
The fractions and are equivalent.
-
and
The fractions and are equivalent.
-
and
The fractions and are NOT equivalent.
-
and
The fractions and are equivalent.
-
and
The fractions and are NOT equivalent.
4.3 Comparing fractions
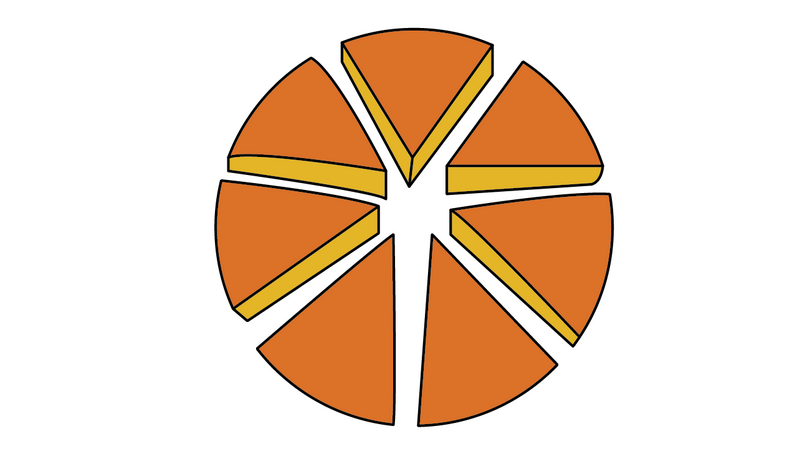
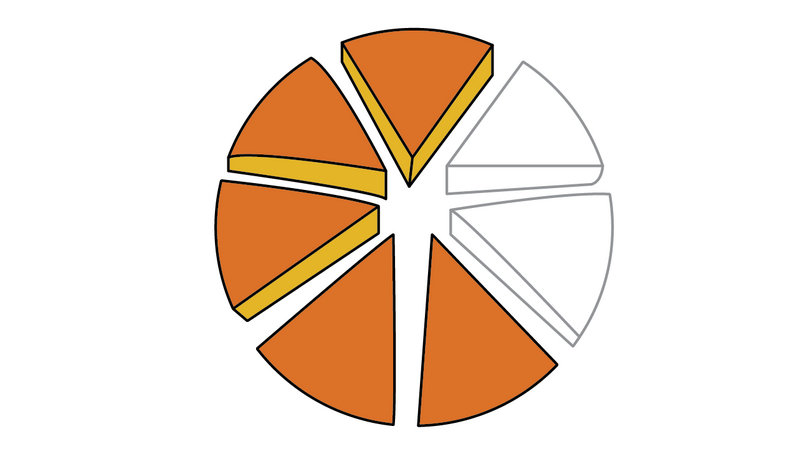
It may be difficult to compare fractions that do not have the same denominator. Look at the two diagrams below. The fraction of the circle that is shaded is given below each diagram.

Which fraction is larger, or ? It is not so easy to decide this just by looking at the diagrams or the fractions themselves. However, if we express both fractions with the same denominator, it becomes easier to compare them.
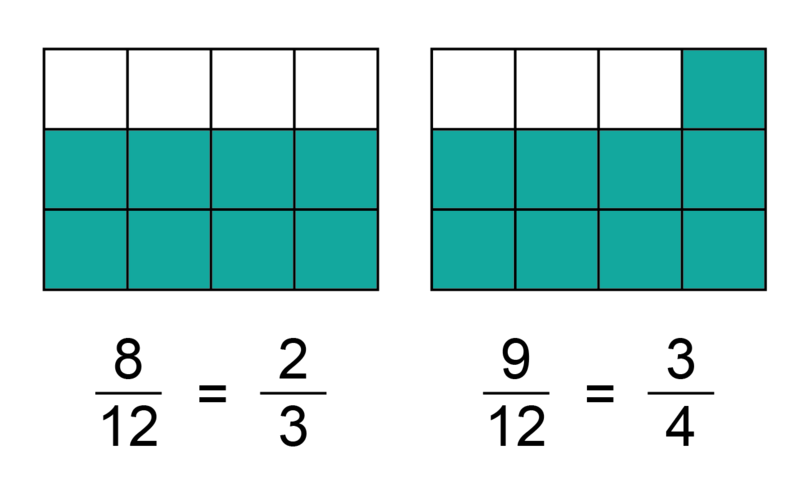
Now it is clear that is the larger fraction. We may write this in two ways:
-
\frac{2}{3}<\frac{3}{4} , which means is smaller than
-
, which means is larger than
To be able to compare fractions, we first need to find the lowest common denominator (LCD) for the fractions. This is the lowest common multiple (LCM) of the denominators. Then we need to express the two fractions as equivalent fractions using this same denominator.
lowest common denominator (LCD) The LCD is the smallest whole number into which the denominators of two or more fractions can divide without a remainder.
If necessary, go back to Chapter 2 to see how to find the LCM of two or more numbers.
If we express more than two fractions using the same denominator, this allows us to order the fractions in ascending order or descending order. Fractions that are arranged in ascending order start with the smallest fraction, then have the next smallest, and so on, and the largest fraction is last. For example . Fractions that are arranged in descending order start with the largest fraction, then have the next largest, and so on, and the smallest fraction is last. For example .
ascending order When numbers of any kind are arranged in ascending order, they are arranged from the smallest to the largest.
descending order When numbers of any kind are arranged in descending order, they are arranged from the largest to the smallest.
Worked example 4.5: Ordering fractions
Arrange the following fractions in ascending order:
-
Step 1: Before we can compare fractions, we need to give equivalent fractions using the same denominator. To do this, first find the LCD of the fractions.
The denominators expressed as products of their prime factors are:
-
Step 2: For each given fraction, find an equivalent fraction using the denominator calculated in Step 1.
-
Step 3: Write the original fractions in the required order.
Ascending order means we have to start with the smallest fraction and end with the largest fraction: .
The original fractions, arranged in ascending order, are:
Exercise 4.6: Order and compare fractions
-
Arrange the following fractions in ascending order:
Ascending order:
-
Arrange the following fractions in descending order:
Descending order:
-
Look at this list of fractions: .
From the list, identify:
- two fractions that are equivalent
- the fraction with the highest value
The proper fractions are all smaller than 1. The two improper fractions are larger than 1, so work only with them.
- the fraction with the lowest value
Both improper fractions are larger than 1. The three proper fractions are smaller than 1, so work only with them.
From a) above:
But:
- an improper fraction that is smaller than 3
From b) above:
\therefore\frac{17}{6}<3- a fraction that is equivalent to
From c) above:
4.4 Decimal fractions
Instead of writing a fraction as a common fraction, we can also write it as a decimal fraction. We use decimal notation to write decimal fractions. In this notation, the numerator is written after a decimal point and the denominator is not written down. Before you can write a common fraction as a decimal fraction, the denominator always has to be a power of ten.
In the first section of this chapter, you learnt that a mixed number is a whole number and a proper fraction. Mixed numbers may also be written in decimal notation. The decimal point separates the whole numbers from the fractions. For example, 2.5 means that we have 2 wholes and a fraction of .
decimal fraction A decimal fraction is a fraction that is written in decimal notation, with the whole number before the decimal point and the fraction after it.
decimal notation Decimal notation is a way of writing a fraction by putting the numerator after a decimal point. The denominator is not written down.
In decimal notation, the number of digits after the decimal point shows us which power of ten is the fraction's denominator. You learnt about these decimal fractions in Chapter 1:
\begin{array}{|l|l|l|l|} \hline \textbf{Name} & \textbf{Common fraction} & \textbf{Powers of ten} & \textbf{Decimal fraction} \newline \hline \text{One tenth} & \frac{1}{10} & \frac{1}{10}=10^{-1} & 0.1 \newline \hline \text{One hundredth} & \frac{1}{100} & \frac{1}{10\times10}=10^{-2} & 0.01 \newline \hline \text{One thousandth} & \frac{1}{1,000} & \frac{1}{10\times10\times10}=10^{-3} & 0.001 \newline \hline \text{One ten thousandth} & \frac{1}{10,000} & \frac{1}{10\times10\times10\times10}=10^{-4} & 0.0001 \newline \hline \end{array}You do not need to write zeros at the end of decimal fractions. For example, we write 0.5 rather than 0.50 or 0.500. This is because .
Converting decimal fractions to common fractions
The fraction 0.5 and the fraction represent exactly the same part of a whole, namely a half. The fractions and are equivalent fractions. A decimal fraction and a common fraction are just different ways of expressing the same value.
Worked example 4.6: Converting decimal fractions to common fractions
Write 4.08 as a common fraction.
-
Step 1: Use the number of digits after the decimal point to determine which power of ten is the denominator.
There are 2 digits after the decimal point. Therefore, the denominator is:
-
Step 2: Starting from the first non-zero digit of the decimal fraction, write the digits without the decimal point. This becomes the numerator of the common fraction.
-
Step 3: Find the simplest form of the fraction obtained in Step 2.
Exercise 4.7: Convert decimal fractions to common fractions
Convert the following decimal fractions to common fractions.
-
1.05
There are 2 digits after the decimal point:
In its simplest form:
-
0.128
There are 3 digits after the decimal point:
In its simplest form:
-
0.0275
There are 4 digits after the decimal point:
In its simplest form:
Converting common fractions to decimal fractions
When a common fraction has a denominator that is a power of ten, it is easy to convert it to a decimal fraction. You dealt with the place values of decimal fractions in Chapter 1.
\begin{array}{|c|c|c|c|c|c|} \hline \text{units} & \text{.} & \text{tenths} & \text{hundredths} & \text{thousandths} & \text{ten thousandths} \newline (1) & \text{.} & \left( \frac{1}{10} \right) & \left( \frac{1}{100} \right) & \left( \frac{1}{1,000} \right) & \left( \frac{1}{10,000} \right) \newline \text{u} & \text{.} & \text{t} & \text{h} & \text{th} & \text{tth} \newline \hline \end{array}Consider the fraction . If the denominator is 1,000, the corresponding decimal fraction must have 3 digits after the decimal point. We may write it in a place value table.
\begin{array}{|c|c|c|c|c|c|} \hline (1) & \text{.} & \left( \frac{1}{10} \right) & \left( \frac{1}{100} \right) & \left( \frac{1}{1,000} \right) & \left( \frac{1}{10,000} \right) \newline \text{u} & \text{.} & \text{t} & \text{h} & \text{th} & \text{tth} \newline \hline 0 & \text{.} & 0 & 3 & 0 & \newline \hline \end{array}The place value table shows that we have zero units, zero tenths, three hundredths and zero thousandths. Remember that we do not write zeros at the end of decimal fraction. This fraction is therefore written as 0.03.
Similarly, the common fraction may be expressed as 0.30, which is written as 0.3. The common fraction may be expressed as 3.0, which is written as 3.
Exercise 4.8: Convert common fractions with denominators that are powers of ten to decimal fractions
Convert the following common fractions to decimal fractions.
-
There must be 3 digits after the decimal point: 0.506
-
There must be 4 digits after the decimal point: 0.0029
-
The must be 2 digits after the decimal point: 7.20
This is written as: 7.2
When the denominator of a common fraction is not a power of ten, we use division to convert the common fraction to a decimal fraction.
Worked example 4.7: Converting common fractions to decimal fractions
Write as a decimal fraction.
-
Step 1: Divide the denominator into the numerator. If it cannot divide, write a zero.
-
Step 2: Put a decimal point after the zero and after the numerator.
-
Step 3: Add zeros after the decimal point in the numerator.
The numbers 5; 5.0; 5.00; 5.000; 5.0000 and so on all represent the value 5.
-
Step 4: Carry on with the division.
-
Step 5: Write down the answer.
The division will carry on forever, because we keep on getting the same remainder. This is called a recurring decimal. We write it with a dot above the digit that repeats.
Exercise 4.9: Convert common fractions to decimal fractions
Convert the following common fractions to decimal fractions.
4.5 Percentages
As well as writing a fraction as a common fraction or a decimal fraction, we may also express a fraction as a percentage. A percentage is a fraction in which the denominator is always 100. Only the numerator is written down, followed by a percentage symbol: %. The symbol shows that the number we wrote down gives the parts of a whole that is divided into 100.
percentage A percentage is a fraction in which the denominator is 100 and where only the numerator is written down, followed by a percentage symbol.
This figure is divided into 100 parts. There are 22 blocks that are shaded. The common fraction tells you what part is shaded. To express this as a percentage, we write only the numerator, followed by a percentage symbol: 22%.
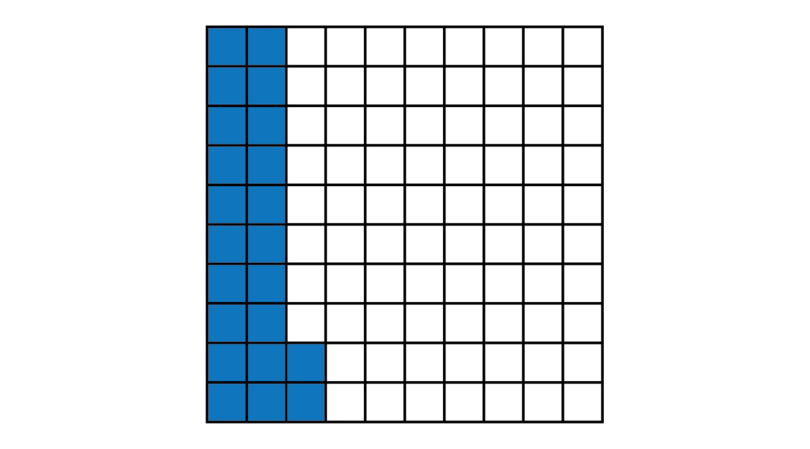
If we shade all the blocks in the figure, the shaded fraction will be . One full whole is therefore 100%.
Converting percentages to common fractions
It is easy to convert percentages to common fractions. We simply use the form . We know that the denominator is always 100, so we have . The numerator is the number before the percentage symbol.
For example, . The simplest form of this fraction is .
Exercise 4.10: Convert percentages to common fractions
Convert the following percentages to common fractions.
-
55%
In its simplest form:
-
80%
In its simplest form:
-
4%
In its simplest form:
Converting common fractions to percentages
To express a common fraction as a percentage, we need to know how many parts out of 100 we are dealing with. Consider the fraction . It shows that we are dealing with 2 parts of a whole that is divided into 5. This square has 100 small blocks in the background, but it is divided into 5 equal rectangles.

We may represent the fraction by shading 2 of the 5 rectangles.

If you count the small blocks that are shaded, you will see that 40 out of the 100 small blocks are shaded. This means that . The fraction has a denominator of 100, so it may be written as a percentage: 40%.
Worked example 4.8: Converting common fractions to percentages
Write as a percentage.
-
Step 1: Find the LCM of 100 and the denominator.
-
Step 2: Find the equivalent fraction in which the denominator is equal to the number obtained in Step 1.
-
Step 3: Simplify the fraction from Step 2 until its denominator is 100.
A common fraction cannot have a decimal fraction as its numerator or denominator. The "fraction" obtained in Step 3 is just used to help us get to the answer.
-
Step 4: Write down the numerator from Step 3, followed by a percentage symbol.
There are other ways to convert common fractions to percentages. You will learn more about this in Chapter 6.
Exercise 4.11: Convert common fractions to percentages
Convert the following common fractions to percentages.
-
-
-
Use long division to determine the numerator:
We keep on getting the same remainder, so this division produces a recurring decimal. We write a dot above the digit that repeats.
4.6 Practical applications
Fractions are very useful in everyday life. We use equivalent fractions to compare different fractions and to convert one type of fraction to another.
Exercise 4.12: Use equivalent fractions to solve problems
-
A teacher has 25 learners in her class. At break time, she decides to give each of them one quarter of an orange to eat. How many oranges does she need?
Parts in one whole: 4
Total parts: 25
She needs oranges.Whole number: 6
Fraction:
She needs oranges. -
After a birthday party, cakes are left over. If the leftover cake is cut into equal pieces, how many people could get one piece each?
Parts in one whole: 5
Parts in 2 cakes:
Additional pieces: 2
Total pieces available: -
The floor of a room is tiled with 64 identical tiles. A carpet is put in the centre of the room. The carpet covers of the tiled surface. How many tiles are under the carpet?
There are 24 tiles under the carpet.
-
A bag with 72 sweets is divided between Musa, Umar and Isa. Musa gets 27 sweets, Umar gets 12 sweets, and Isa gets the rest of the sweets. Determine which fraction of the bag each boy received.
Musa:
Umar:
Isa received sweets:
-
Atinuke and Eniola buy a bag of rice. Atinuke gets of the bag, Eniola gets of the bag and a little bit is left over. Who received the larger portion of rice, Atinuke or Eniola?
Eniola received the larger portion of the rice.
-
A wall with a surface area of 1 m is painted. The painter knocks over the can of paint and some of the paint cannot be recovered. She is only able to paint 0.85 m of the wall. Express the fraction of the wall that was painted as a common fraction.
There are 2 digits after the decimal point:
-
Amadi has to walk 1 km to school. After walking of the way, he realises that he forgot a book at home and he turns around. Determine the distance Amadi walked before he turned around. Give the answer in kilometres.
Amadi walked 0.625 km before he turned around.
-
Jummai got 88% for a class test. The test was for 25 marks. Calculate Jummai's mark out of 25.
Jummai's mark was 22 out of 25.
-
There are 30 students in a class. If 21 students are girls, what percentage of the class is female?
Fraction of the class that is female:
70% of the class is female.
-
A children's clothing store advertises a 15% discount on a dress of ₦3,000. Calculate the value of the discount.
The discount is ₦450.
4.7 Summary
- A common fraction is a fraction that is written in the form , where the numerator and denominator are both whole numbers.
- A proper fraction is smaller than 1. The numerator is smaller than the denominator, for example .
- A mixed number consists of a whole number and a proper fraction, for example .
- An improper fraction is larger than 1. The numerator is larger than the denominator, for example .
- Equivalent fractions have different numerators and denominators, but they represent the same part of a whole and therefore the same value. For example, .
- A fraction is in its simplest form when the numerator and denominator have no common factor.
- To be able to compare fractions, we must express them with the same denominators. The lowest common denominator (LCD) of two or more fractions is the smallest whole number into which all the denominators can divide without a remainder.
- A decimal fraction is a fraction expressed in decimal notation, where the numerator is written after a decimal point and the denominator is not written down. The denominator in a decimal fraction must be a power of ten.
- In decimal notation, the decimal point separates whole numbers from fractions.
- In decimal notation, the number of digits after the decimal point shows us which power of ten is the fraction's denominator. For example, if there are three digits after the decimal point, the denominator is .
- A percentage is a fraction of which the denominator is 100 and where only the numerator is written down, followed by a percentage symbol.