Chapter 15: Angles
In this chapter you will work with angles. You will learn how to label and measure angles. You will also learn about the different angles that are formed on a straight line when straight lines cross each other.
angle An angle is the amount of turn between two straight lines that have a common end point. The common end point is called the vertex of the angle.
15.1 Labelling and measuring angles
We measure angles in degrees. Before we can measure angles, we need to know how to label angles.
Labelling angles
When we label an angle, we name the angle, so that we know which angle it is that we are talking about.
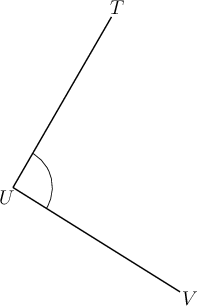
Worked example 15.1: Labelling angles
Consider the following diagram.
Give the correct label for the marked angle.
-
Step 1: Remember that there are three different ways to indicate an angle.
- We may indicate an angle with a above the name of the point where the angle is formed.
- We may show in front of the name of the point.
- We may use the names of the lines that form the angle.
-
Step 2: Find the marked angle on the the diagram.
There is only one angle at point .
-
Step 3: Give the correct answer.
We can label this angle as or .
We could also label this angle as or .
To use the names of the lines that form the angle, trace over the angle with your finger, and label the angle in the order of line labels that you followed.
From now on we will use only one notation. We will label the angle at point as .
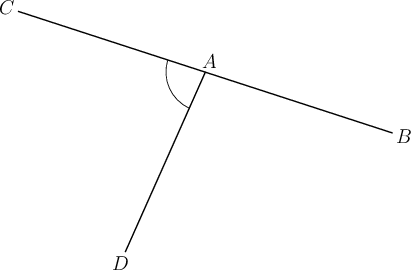
Worked example 15.2: Labelling angles
Consider the following diagram.
Give the correct label for the marked angle.
-
Step 1: Find the marked angle in the diagram.
There are two different angles at point . If we just write , it will be unclear which angle we mean.
To make sure that we are understood correctly, we have to label the marked angle using the names of the lines that form it.
-
Step 2: Give the correct answer.
The marked angle can be labelled as or .
It is easy to make a mistake if you have to refer to an angle as or . It is also time consuming, so we often use small numbers to label angles. We use these to refer more easily to a specific angle. You can tell that these small numbers are not the sizes of the angles, as they are not labelled with the degree symbol (and the numbers are much too small).
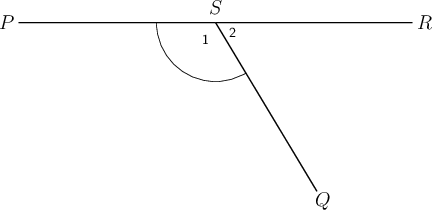
Worked example 15.3: Labelling angles
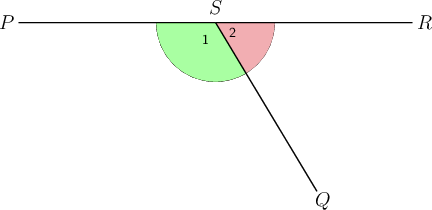
Consider the following diagram.
Give the correct label for the marked angle.
-
Step 1: Find the marked angle in the diagram.
There are two different angles at point , so if we just write it will be unclear which angle we mean.
Ask yourself the following: At what point and number is the marked angle?
-
Step 2: Give the correct answer.
To make sure that we are understood, we use the point label and the relevant number ( ) to label the angle as .
It would also be correct to label the angle as or . However, we do not label angles as , because it is not necessary to use both the angle number and all three line labels.
Exercise 15.1: Label angles
-
Consider the following diagram. Give the correct label for the marked angle.
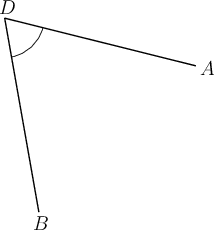
There is only one angle at point , so we can label this angle as without any confusion. We could also label this angle as or . If you trace your finger over the points in this order, you will draw the angle.
-
Consider the following diagram. Give the correct label for the marked angle.
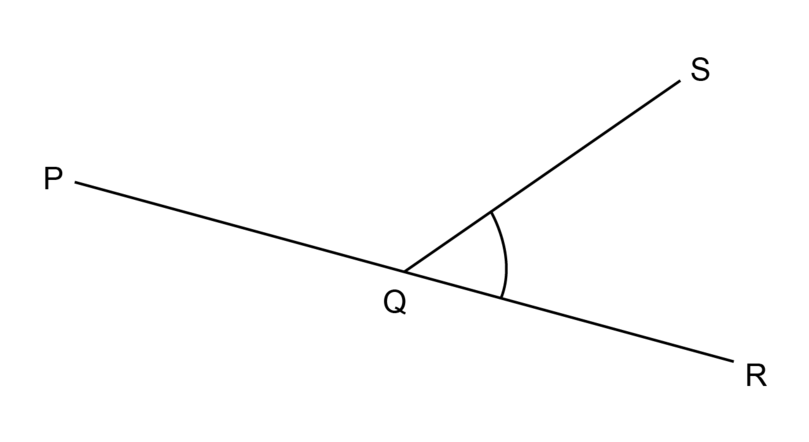
There are two different angles at point . If we just write it will be unclear which angle we mean.
The marked angle can be labelled as or .
-
Consider the following diagram. Give the correct label for the marked angle.
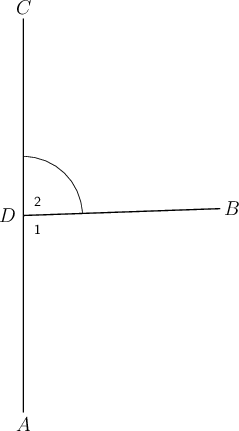
There are two different angles at point . If we just write it will be unclear which angle we mean.
We use the point label and the relevant number ) to label the angle as .
-
Consider the following diagram. Give the correct label for the marked angle.
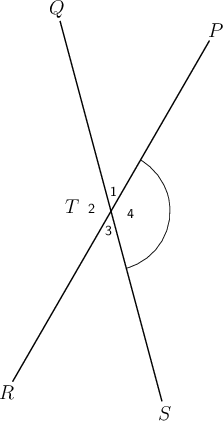
There are four different angles at point . If we just write it will be unclear which angle we mean.
To make sure that we are understood, we use the point label and the relevant number ( ) to label the angle as .
-
Consider the following diagram. How would you mark ?

Measuring angles
We measure angles in degrees. We use a protractor to measure an angle.

Take note of the following when you use a protractor:
-
A protractor has a centre, which can also be called the origin.

When you measure an angle you have to make sure that the centre (or origin) of the protractor is exactly on the vertex of the angle that you want to measure.
-
The centre (or origin) of a protractor is on the base line of the protractor.

When you measure an angle you also have to make sure that one side of the base line of the protractor is exactly on one of the arms of the angle that you want to measure.
-
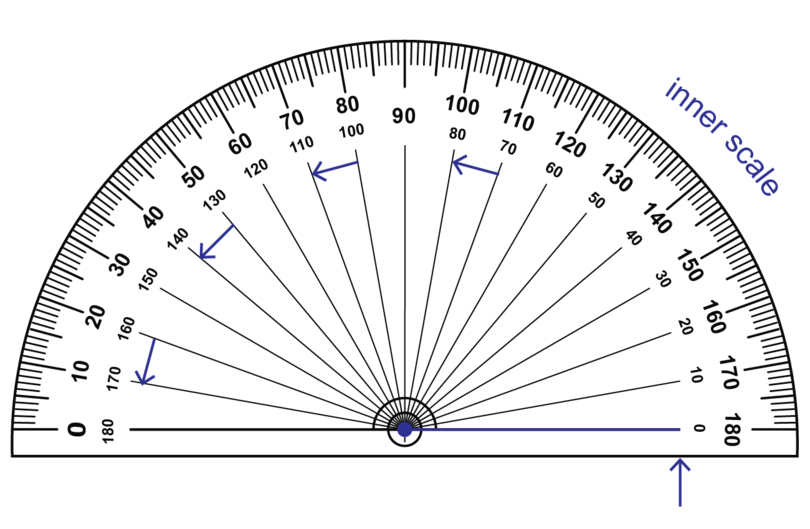
There are two zeroes on a protractor.
If you begin measuring from the zero on the left hand side of the protractor, you use the outer scale on the protractor.
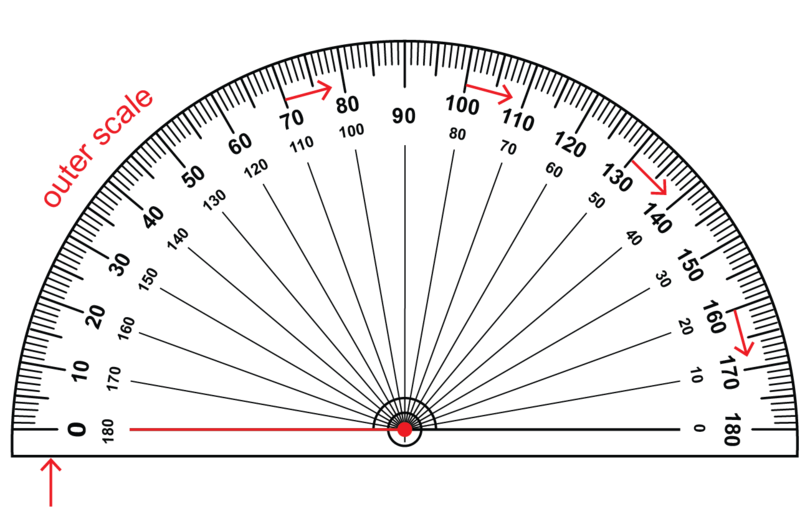
If you begin measuring from the zero on the right hand side of the protractor, you use the inner scale on the protractor.
It is a good idea to estimate the size of an angle before you measure the angle. Then you can be sure that you are reading off the correct answer from the protractor.
Types of angles
Different types of angles have different names. The names you may need to use when working with angles are given in the table below.
| Name of angle | Size of angle |
|---|---|
| acute angle | between and |
| right angle | |
| obtuse angle | between and |
| straight angle | |
| reflex angle | between and |
| revolution |
Worked example 15.4: Measuring a right angle
Use a protractor to measure the given angle in the diagram below.
-
Step 1: Consider the diagram and estimate the size of the angle.
The diagram shows two arms: and . It seems as if they form a right angle, which is shaded green. A right angle is equal to .
-
Step 2: Place the protractor correctly on the angle.
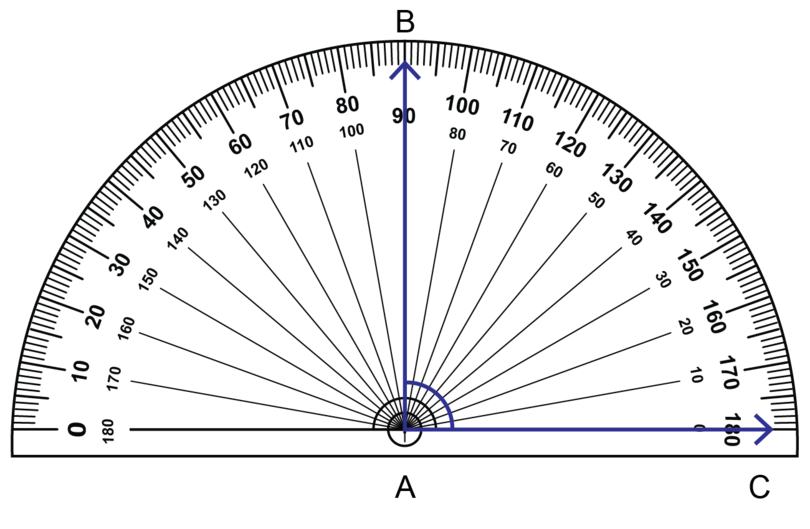
- The centre of the protractor should be on the vertex of the angle.
- The base line of the protractor should be on one arm of the angle.
-
Step 3: Choose the scale you will use.
The arm on which the base line lies is to the right side of the protractor. On the right side, it is the inner scale that starts from 0, so use the inner scale.
-
Step 4: Read off the size of the angle from the protractor, and give the answer. Name the angle correctly, and remember to include the degree symbol.
Worked example 15.5: Measuring an acute angle
Use a protractor to measure the marked angle shown below.
-
Step 1: Consider the diagram and estimate the size of the angle.
The angle shaded red is between two arms: and . It seems that the marked angle is an acute angle.
An acute angle is between and . This angle is nearer to than to .
-
Step 2: Place the protractor correctly on the angle.
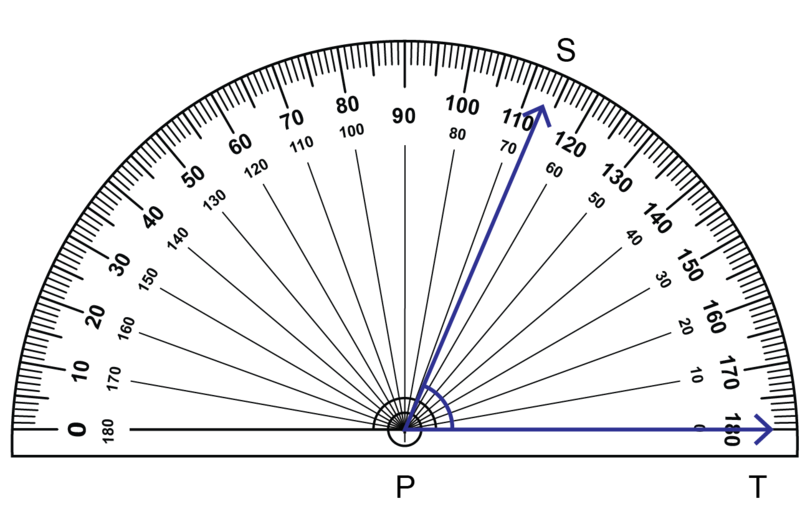
- The centre of the protractor should be on the vertex of the angle.
- The base line of the protractor should be on one arm of the angle.
-
Step 3: Choose the correct scale.
The arm on which the base line lies is to the right side of the protractor, so use the inner scale.
-
Step 4: Read off the size of the angle from the protractor, and check against your estimation.
is an acute angle, and is closer to than to .
-
Step 5: Name the angle, and give the answer.
Worked example 15.6: Measuring an obtuse angle
Use a protractor to measure the marked angle shown below.
Use the dotted lines shown to help with your estimation. The dotted lines have a angle between them.
-
Step 1: Consider the diagram and estimate the size of the angle.
The diagram shows two arms: and . It seems as if they form an obtuse angle, which is shaded red. An obtuse angle is between and . This angle is almost a full straight angle, so it must be very close to .
-
Step 2: Place the protractor correctly on the angle.
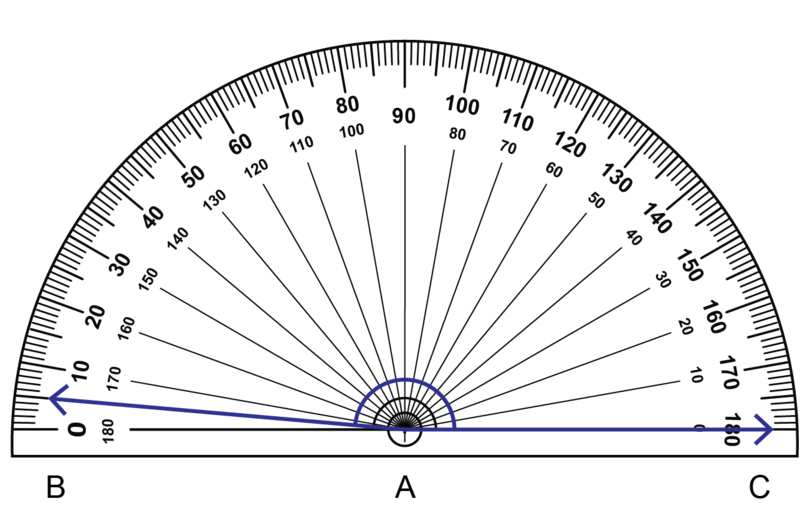
- The centre of the protractor should be on the vertex of the angle.
- The base line of the protractor should be on one arm of the angle.
-
Step 3: Choose the correct scale.
The arm on which the base line lies is to the right side of the protractor, so use the inner scale.
-
Step 4: Read off the size of the angle from the protractor, and check against your estimation.
is an obtuse angle, and is close to .
-
Step 5: Name the angle, and give the answer.
Worked example 15.7: Measuring a reflex angle
Use a protractor and measure the angle shown below.
-
Step 1: Consider the diagram and estimate the size of the angle.
The diagram shows two arms: and . They form a reflex angle, which is shaded red.
A reflex angle is between and . This angle is very near to .
-
Step 2: Find a way to measure this reflex angle.
An ordinary protractor can only measure angles between to . We cannot measure a reflex angle with an ordinary protractor. We have to measure the angle that is not shaded and then subtract the answer from .
-
Step 3: Place the protractor correctly on the angle to measure.
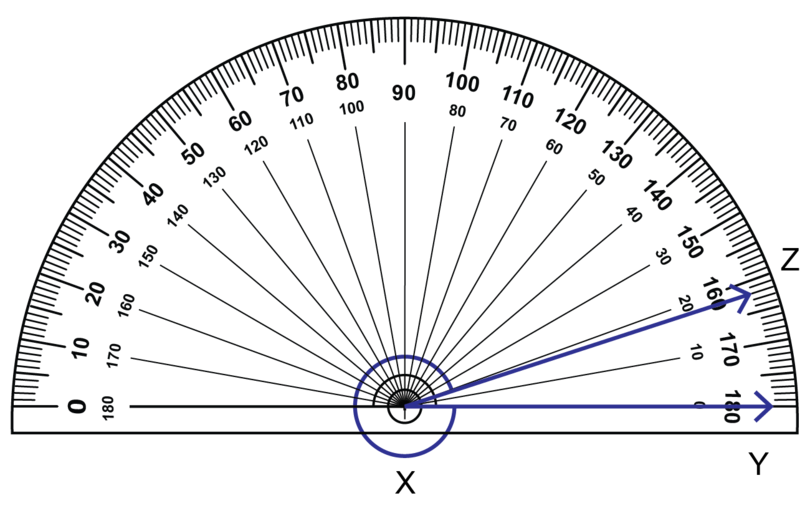
- The centre of the protractor should be on the vertex of the angle.
- The base line of the protractor should be on one arm of the angle.
-
Step 4: Choose the scale and read off the size of the angle.
The acute angle measures .
-
Step 5: Subtract the measured angle from and give the correct answer. Check against your estimation, and name the reflex angle correctly.
\begin {align} \text{Reflex } Z\hat{X}Y &= 360^{\circ} - 18^{\circ}\\ &= 342^{\circ} \end {align}
Remember that reflex angles are always less than , but more than . A full turn or revolution is equal to .
Exercise 15.2: Measure angles
-
Use a protractor and measure the angle shown below.

Estimate the size of the angle: The angle is an acute angle, so the measurement should be between and .
Measure the angle with a protractor.
Answer: -
Use a protractor and measure the angle shown below.

Estimate: acute angle, so between and
Answer: -
Use a protractor and measure the angle shown below.

Estimate: obtuse angle, so between and
Answer: -
Use a protractor and measure the angle shown below.

Estimate: obtuse angle, so between and
Answer: -
Use a protractor and measure the angle shown below.

Estimate: reflex angle, so between and
Measure the angle that is not shaded and then subtract the answer from .
Acute
Subtract to find the size of the reflex angle:
\begin {align} \text{Reflex } Z\hat{X}Y & =360^{\circ} - 70^{\circ}\\ &= 290^{\circ} \end {align} -
Use a protractor and measure the angle shown below.
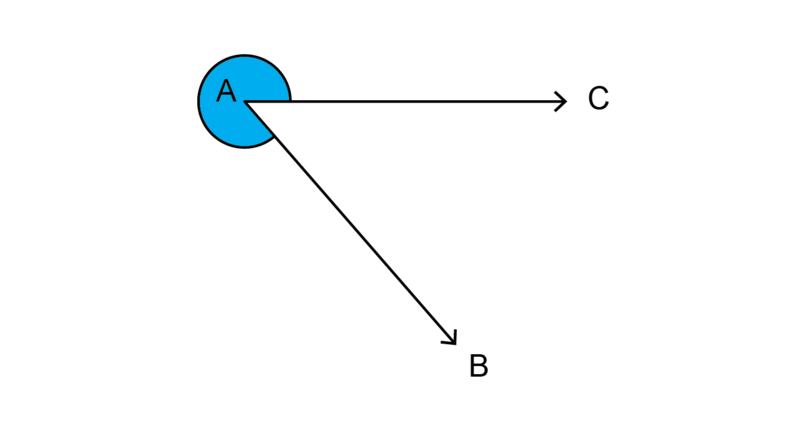
Estimate: reflex angle, so between and
Measure the angle that is not shaded and then subtract the answer from .
Acute
Subtract to find the size of the reflex angle:
\begin {align} \text{Reflex } C\hat{A}B &= 360^{\circ} - 49^{\circ}\\ &= 311^{\circ} \end {align}
15.2 Angles on straight and intersecting lines
You will need to to be able to identify and measure angles on a straight line as well as angles formed by two intersecting lines. When you know the properties of these angles, you can use them to solve problems that involve angles and lines.
Angles on a straight line
A straight line is also called a straight angle. A straight angle is equal to . If a straight line is formed by more than one angle, the sum of those angles will be . We say the angles are supplementary angles.
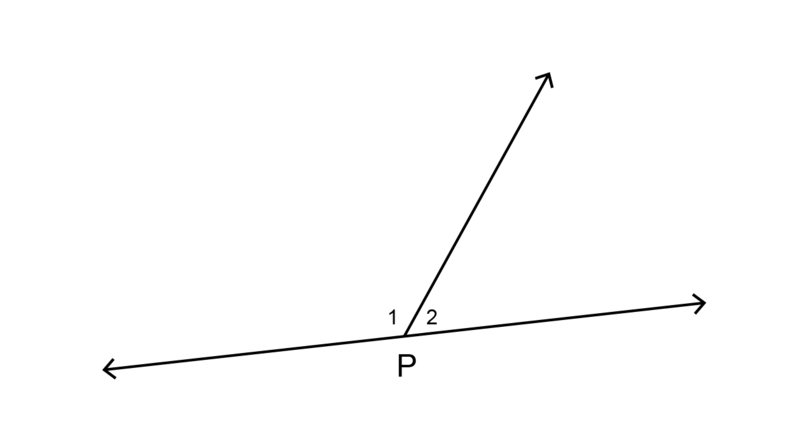
In the diagram above, the two angles are supplementary angles, because they form a straight line. + =
We can also say that the two angles in the diagram above are adjacent angles.
Adjacent angles are next to each other. Two adjacent angles share the same vertex and they also share one common arm.
In the diagram below and have the same vertex, but they do not share a common arm.

and are NOT adjacent angles, because they do not share a common arm.
Adjacent angles do not always have to be supplementary. In the diagram below the two angles are adjacent, but they do not add up to .
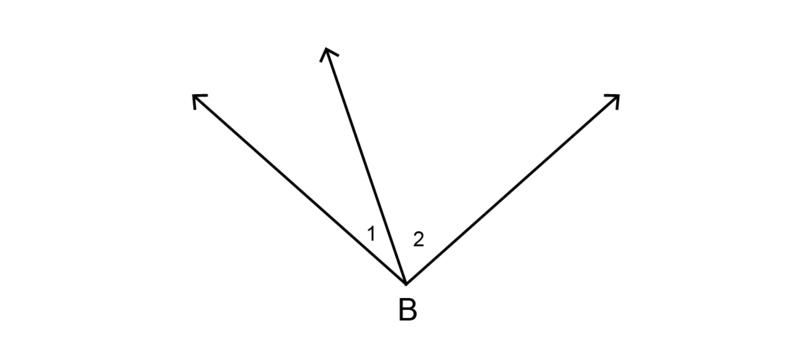
supplementary angles Two (or more) angles are supplementary if they add up to .
adjacent angles Adjacent angles are next to each other. Two adjacent angles share the same vertex and a common arm.
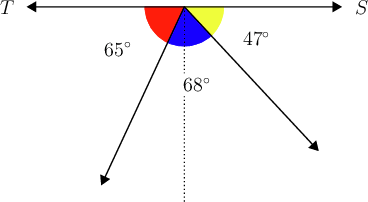
Worked example 15.8: Calculating angles on a straight line
Consider the diagram given below. You are given the following information:
- is a straight line
- =
- =
- =
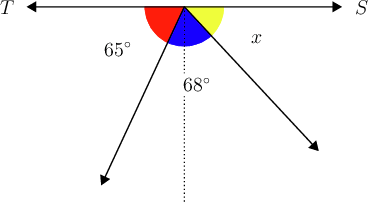
What is the value of ?
-
Step 1: Read the given information and consider the diagram carefully.
Begin the answer by writing down the facts you know.
The angles must have a sum of , because they form a straight line.
-
Step 2: Substitute all the values, including the unknown value, .
\begin{align} a + b + c & = 180^{\circ} \\ 65^{\circ} + 68^{\circ} + x & = 180^{\circ} \\ \end{align} -
Step 3: Solve the equation.
\begin{align} a + b + c & = 180^{\circ} \\ 65^{\circ} + 68^{\circ} + x & = 180^{\circ} \\ 133^{\circ} + x & = 180^{\circ}\\ x & = 180^{\circ} - 133^{\circ}\\ \therefore x & = 47^{\circ} \\ \end{align}You could now complete the diagram by replacing the .
When we refer to lines and line segments we can use different notations:
- means the line segment from point to point .
- means the line through points and .
- Most of the time we simply write for the line through point and point and also for the line segment from point to point .
Exercise 15.3: Calculate angles on a straight line
-
is a straight line, with angles as shown in the diagram below.
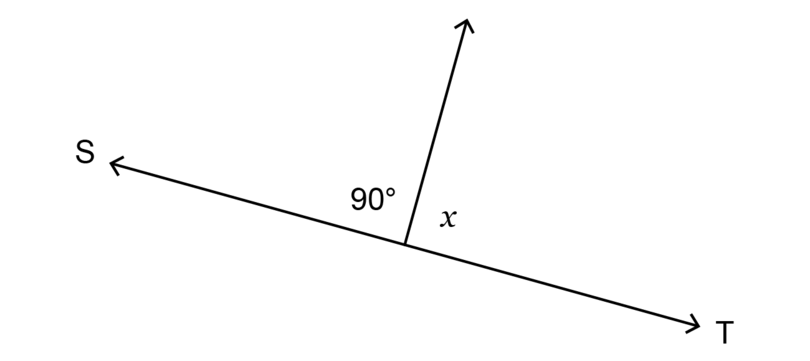
What is the value of ?
The angles must have a sum of , because they form a straight line.
\begin{align} 90^{\circ} + x & = 180^{\circ} \\ \therefore x & = 90^{\circ} \\ \end{align} -
is a straight line, with angles as shown below.
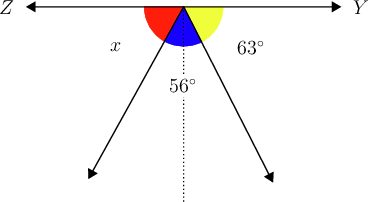
What is the value of ?
The angles must have a sum of , because they form a straight line.
\begin{align} x + 56^{\circ} + 63^{\circ} & = 180^{\circ} \\ x + 119^{\circ} & = 180^{\circ}\\ \therefore x & = 61^{\circ} \\ \end{align} -
is a straight line, with angles as shown below.
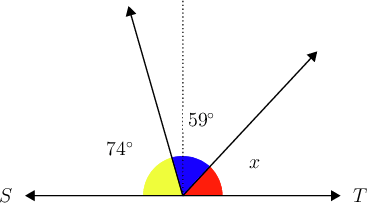
What is the value of ?
The angles must have a sum of , because they form a straight line.
\begin{align} x + 59^{\circ} + 74^{\circ} & = 180^{\circ} \\ x + 133^{\circ} & = 180^{\circ}\\ \therefore x & = 47^{\circ} \\ \end{align}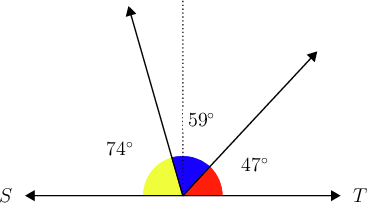
-
Examine the diagram below, and answer the two questions that follow.
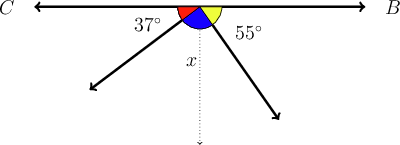
- Calculate .
- What type of angle is represented by ?
The angles must have a sum of , because they form a straight line.
\begin{align} 37^{\circ} + x + 55^{\circ} & = 180^{\circ} \\ 92^{\circ} + x & = 180^{\circ}\\ \therefore x & = 88^{\circ} \\ \end{align}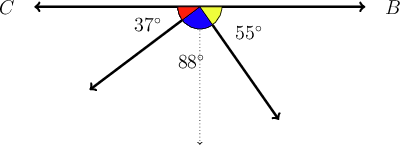
The angle represented by is an acute angle.
-
Examine the diagram below, and answer the questions that follow.
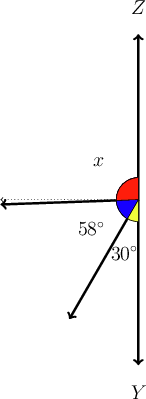
- Calculate .
- What type of angle is represented by ?
The angles must have a sum of , because they form a straight line.
\begin{align} x + 58^{\circ} + 30^{\circ} & = 180^{\circ} \\ x + 88^{\circ} & = 180^{\circ}\\ \therefore x & = 92^{\circ} \\ \end{align}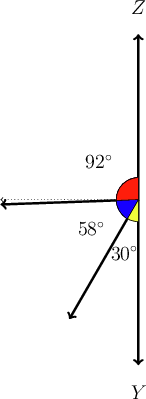
The angle represented by is an obtuse angle.
-
Examine the diagram below, and answer the two questions that follow.
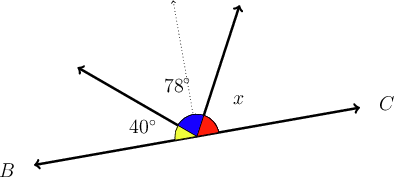
- Calculate .
- What type of angle is represented by ?
The angles must have a sum of , because they form a straight line.
\begin{align} x + 78^{\circ} + 40^{\circ} & = 180^{\circ} \\ x + 118^{\circ} & = 180^{\circ} \\ \therefore x & = 62^{\circ} \\ \end{align}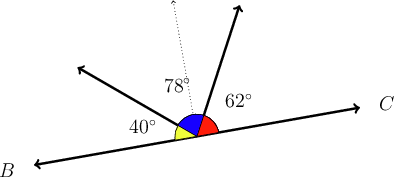
The angle represented by is an acute angle.
-
In the diagram below, line is a straight line with angles labelled above and below it.

Find the values of and , giving reasons for your answer. (Remember to check your answers.)
All of the angles above add up to :
\begin{align} x + 65^{\circ} + 60^{\circ} & = 180^{\circ} \quad(\text{angles on a straight line}) \\ x + 125^{\circ} & = 180^{\circ}\\ x & = 180^{\circ} - 125^{\circ}\\ \therefore x & = 55^{\circ} \\ \end{align}In the same way, all of the angles below add up to :
\begin{align} 26^{\circ} + 82^{\circ} + 35^{\circ} + y & = 180^{\circ} \quad(\text{angles on a straight line}) \\ 143^{\circ} + y & = 180^{\circ} \\ y & = 180^{\circ} - 143^{\circ} \\ \therefore y & = 37^{\circ} \\ \end{align}
The angles in a full turn (revolution) must add up to . This is a good way to check your answers:
\begin{align} 55^{\circ} + 65^{\circ} + 60^{\circ} + 26^{\circ} + 82^{\circ} + 35^{\circ} + 37^{\circ} & = 360^{\circ} \\ \end{align} -
In the diagram below, is a straight line with angles labelled above and below it.
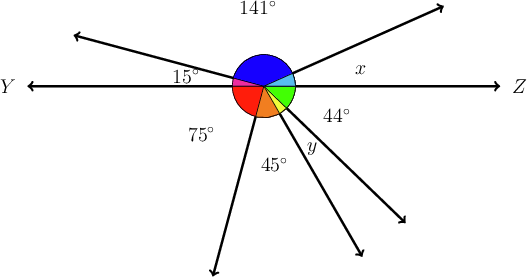
Find the values of and , giving reasons for your answer. (Remember to check your answers.)
All of the angles above add up to :
\begin{align} 15^{\circ} + 141^{\circ} + x & = 180^{\circ}\quad(\text{angles on a straight line}) \\ 156^{\circ} + x & = 180^{\circ}\\ x &= 180^{\circ} - 156^{\circ}\\ \therefore x & = 24^{\circ} \\ \end{align}In the same way, all of the angles below add up to :
\begin{align} 44^{\circ} + y + 45^{\circ} + 75^{\circ} & = 180^{\circ} \quad(\text{angles on a straight line}) \\ 164^{\circ} + y & = 180^{\circ}\\ y & = 180^{\circ} - 164^{\circ}\\ \therefore y & = 16^{\circ} \\ \end{align}Here is the completed diagram, with all of the angle values labelled:
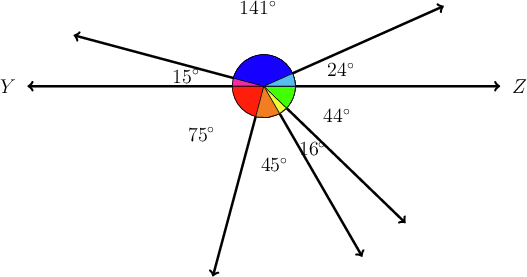
Check your answers:
\begin{align} 15^{\circ} + 141^{\circ} + 24^{\circ} + 44^{\circ} + 16^{\circ} + 45^{\circ} + 75^{\circ} & = 360^{\circ} \\ \end{align}
You will not usually be asked to redraw the diagram to give the missing angle size.
Angles at intersecting lines
When two lines cross each other, we say the two lines are intersecting lines.
intersecting lines Intersecting lines are lines that cross each other.
The diagram shows two straight lines intersecting at a point, and forming the four angles , , and .

Two types of angles are formed by the intersecting lines.
-
Adjacent angles: Adjacent angles are angles that are next to each other. They have the same vertex and they share a common arm.
In the diagram below the following angles are adjacent angles:
- and are adjacent
- and are adjacent
- and are adjacent
- and are adjacent

In each case, these pairs of adjacent angles form a straight line, so they are also supplementary.
Supplementary angles add up to . So, in this case we can also say:
- + =
- + =
- + =
- + =
-
Vertically opposite angles: Two intersecting straight lines form vertically opposite angles.
Vertically opposite angles have the same vertex, but they are on opposite sides of the vertex.
Vertically opposite angles are equal to each other.

In the diagram above:
- = because they are vertically opposite angles.
- = because they are vertically opposite angles.
vertically opposite angles Vertically opposite angles are on the opposite sides of a vertex formed by two intersecting lines. Vertically opposite angles are equal to each other.
The four angles formed by two intersecting straight lines form a revolution. All the angles around one point form a revolution. One revolution is equal to .
+ + + =
We can also use Greek letters to label angles:
- We read as "alpha ".
- We read as "beta ".
- We read as "delta ".
Worked example 15.9: Identifying types of angles at intersecting lines
The diagram shows line intersecting line . The intersecting lines create four different angles. These angles are labelled with the variables , , , and .

Which angle or angles are adjacent to ?
-
Step 1: Consider the diagram and remember the definition for adjacent angles.
Adjacent angles are angles that are next to each other.

-
Step 2: Identify the angle or angle that are adjacent to .
There are two such neighbours: and .
-
Step 3: Give the correct answer.
and are adjacent to .
Which angle is vertically opposite ?
-
Step 1: Consider the diagram and remember the definition for vertically opposite angles.
Vertically opposite angles are angles that share a vertex and are opposite each other.

-
Step 2: Identify the angle that is vertically opposite , and give the correct answer.
is vertically opposite .
Exercise 15.4: Identify angles at intersecting lines
The diagram shows line intersecting line . The intersecting lines create four different angles. These angles are labelled , , , and .
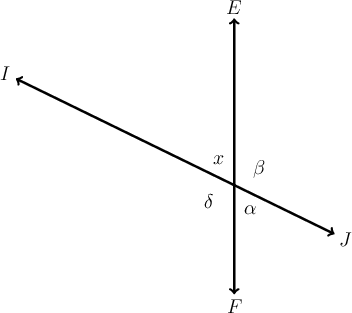
-
Which angle or angles are supplementary to ?
Supplementary angles form a straight line.
and are supplementary.
and are supplementary.
-
Which angle or angles are adjacent to ?
Adjacent angles share the same vertex and a common arm.
is adjacent to .
is adjacent to .
-
Name two pairs of vertically opposite angles.
Vertically opposite angles share the same vertex and are on opposite sides of the vertex.
and are vertically opposite angles.
and are vertically opposite angles.
-
Say whether the following statement is true or false: =
and are vertically opposite angles and vertically opposite angles are equal.
The statement is true.
-
Say whether the following statement is true or false: + + + =
The angles around a point form a revolution and a revolution is equal to (not ).
The statement is false.
Using the properties of angles at intersecting lines in calculations
Now that you know how to identify the different angles formed by two intersecting straight lines, you can use these angles and their properties to do calculations. These will involve working out the value of unknown angle sizes.
When you look at a diagram of two intersecting lines, you have to remember all the facts that you have learnt about intersecting straight lines. Then decide which one you would use to solve the problem.
In geometry, it is as important to give a reason for your answer as it is to find the size of the angle. We write the reasons in a shorter form.
The shorter form of the straight line facts are given in brackets:
- Adjacent angles on a straight line add up to : (adj s on str line)
- Vertically opposite angles are equal: (vert opp s)
- Angles around a point add up to : ( s around a pt)
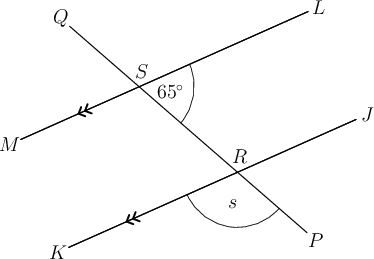
Worked example 15.10: Using properties of intersecting straight lines
In the diagram below, and are straight lines.
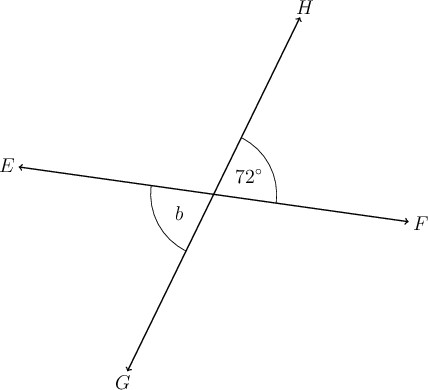
Determine the value of , giving a reason for your answer.
-
Step 1: Consider the diagram.
and are straight lines, which means that they form vertically opposite angles when they intersect. Vertically opposite angles are equal.
-
Step 2: Determine the value of .
We know that is equal to because the two angles are vertically opposite angles.
-
Step 3: Give the correct answer with its shortened reason in brackets.
(vert opp s)
Exercise 15.5: Calculate angles at intersecting straight lines
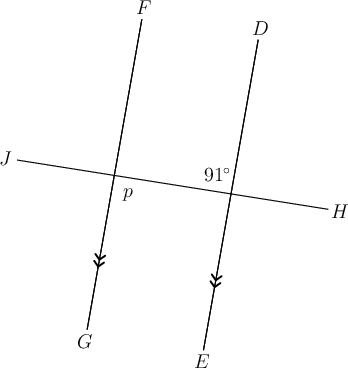
-
In the diagram below, and are straight lines.
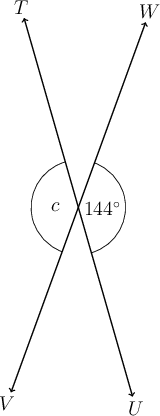
Determine the value of , giving a reason for your answer.
(vert opp s)
-
In the diagram below, and are straight lines.
Determine the value of , giving a reason for your answer.
(vert opp s)
-
In the diagram below, and are straight lines.

Determine the value of , giving a reason for your answer.
The angle is not vertically opposite , so we can just ignore it.
(vert opp s) -
In the diagram below, and are straight lines.

Determine the value of , giving a reason for your answer.
The angle is not vertically opposite , so we can just ignore it.
(vert opp s) -
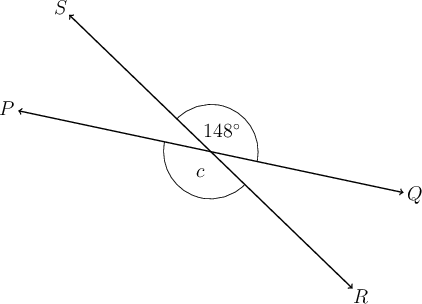
In the diagram below, and are straight lines.

Determine the value of , giving a reason for your answer.
\begin{align} p + 83^{\circ} & = 142^{\circ} (\text {vert opp} \angle s) \\ p & = 142^{\circ} - 83^{\circ}\\ p & = 59^{\circ} \end{align}
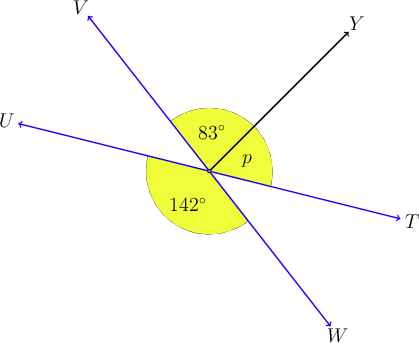
(vert opp s)
15.3 Angles on parallel lines
Parallel lines are always the same distance apart. We use arrow markings to indicate parallel lines, as shown below.
- The two lines that have a single arrow are parallel to each other.
- The two lines that have a double arrow are parallel to each other.
In writing we use two vertical lines to indicate that two lines are parallel:
A transversal is a line that crosses two or more parallel lines. In the diagram below, and is a transversal.
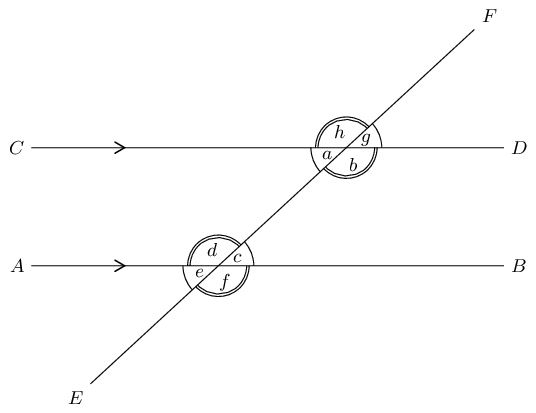
transversal A transversal is a line that intersects two or more parallel lines.
The diagram shows that the transversal intersects the parallel lines and .
The intersecting lines create angles. Some of these angles are labelled.
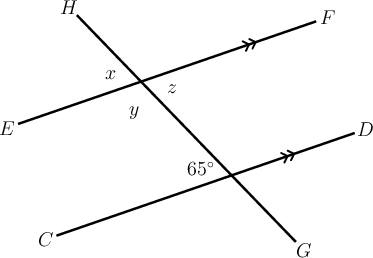
If the two lines are parallel, the four angles around the first intersection are the same as the four angles around the second intersection. We can use this to determine the unknown angles.
- is in the same position as the angle of , so .
- and are angles on a straight line, so = .
- and are vertically opposite angles, so = .
We can fill in the sizes of all the angles on the diagram:

We give special names to the angles formed by two parallel lines and a transversal. There are three types of angles that you should learn to recognise:
-
Corresponding angles: Corresponding angles are in matching positions on the parallel lines. They are on the same side of the parallel lines, and on the same side of the transversal.
If we colour the lines that make corresponding angles, we will see an "F " shape. This helps us to identify corresponding angles.
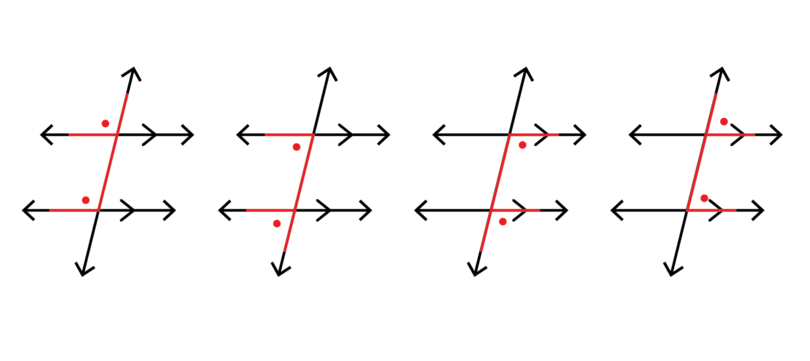
Corresponding angles are equal, but only if the lines cut by the transversal are parallel.
-
Co-interior angles: Co-interior angles are both inside the parallel lines, and on the same side of the transversal.
If we colour the lines that make co-interior angles, we will see a "U " shape. This helps us identify co-interior angles.
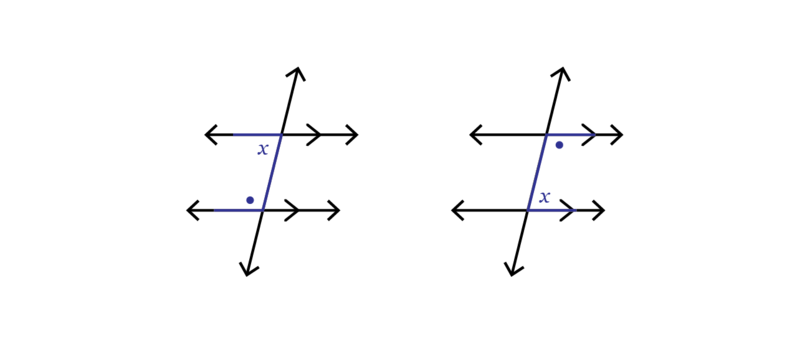
Co-interior angles add up to , but only if the lines cut by the transversal are parallel.
-
Alternate angles: Alternate angles are both inside the parallel lines, but on different sides of the transversal.
If we we colour the lines that make alternate angles, we will see an "N " shape. This helps us identify alternate angles.
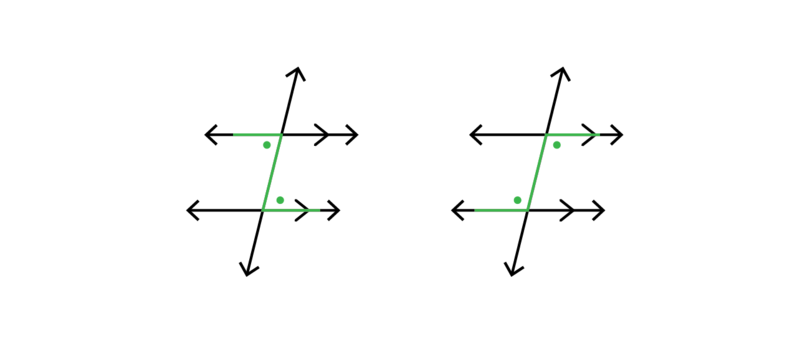
Alternate angles are equal, but only if the lines cut by the transversal are parallel.
corresponding angles Corresponding angles are equal. They are in matching positions on the parallel lines and transversal, in an "F " shape.
co-interior angles Co-interior angles are supplementary. They are both inside the parallel lines and on the same side of the transversal, in a "U " shape.
alternate angles Alternate angles are both inside the parallel lines and on different sides of the transversal, in an "N " shape.
To help you remember these angles, think of Maths is FUN!.
If two parallel lines are cut by a transversal, then:
- F: corresponding angles are equal
- U: co-interior angles are supplementary
- N: alternate angles are equal
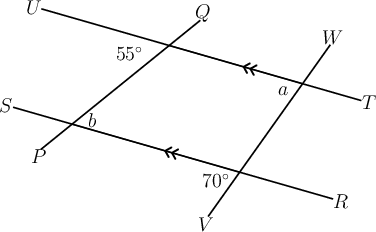
Worked example 15.11: Recognising pairs of angles between parallel lines
In the diagram below, and is a transversal.
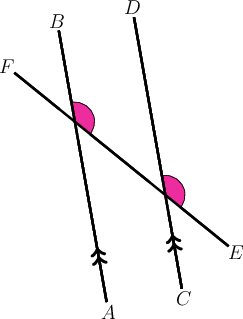
What type of angle pair is shown by the shaded angles? What is the relationship between the two angles?
-
Step 1: Consider the diagram and remember the three types of angles formed by two parallel lines and a transversal.
F: corresponding angles are equal
U: co-interior angles are supplementary
N: alternate angles are equal
-
Step 2: Identify the type of angle pair.
If we draw a shape around the angles, we will see an "F " shape. This helps us to identify corresponding angles.
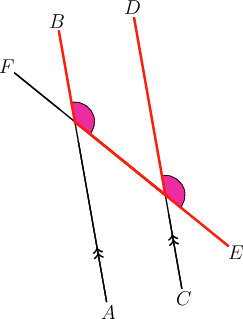
-
Step 3: Give the correct answers.
The shaded angles are corresponding angles.
The corresponding angles are equal because .
Exercise 15.6: Recognise pairs of angles between parallel lines
-
In the diagram below, and is a transversal.
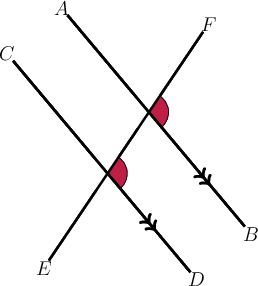
What type of angle pair is shown by the shaded angles?
What is the relationship between the two angles?
If we highlight the angles we will see an "F " shape.
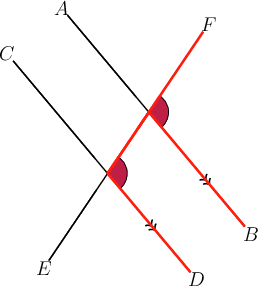
The shaded angles are corresponding angles.
The corresponding angles are equal because .
-
In the diagram below, and is a transversal.
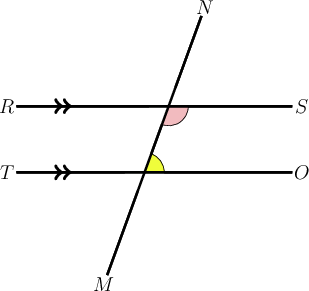
What type of angle pair is shown by the shaded angles?
What is the relationship between the two angles?
If we highlight the angles we will see a "U " shape.
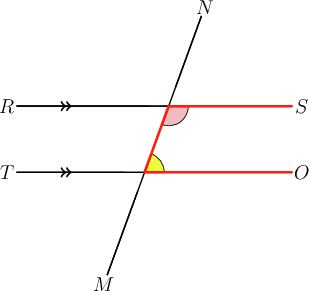
The shaded angles are co-interior angles.
The co-interior angles are supplementary because .
-
In the diagram below, and is a transversal.

What type of angle pair is shown by the shaded angles?
What is the relationship between the two angles?
If we highlight the angles we will see an "N " shape.

The shaded angles are alternate angles.
The alternate angles are equal because .
Using the properties of angles on parallel lines in calculations
Now that you know about corresponding angles, co-interior angles and alternate angles, you can use the properties of these angles to solve problems.
Worked example 15.12: Calculating angles between parallel lines
In the diagram below, and is a transversal.
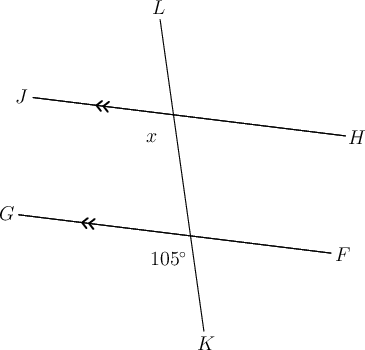
What is the value of ? Give a reason for your answer.
-
Step 1: Consider the diagram and remember the F-U-N angles.
Recognise the position of the angles marked and .
The angles are in matching positions, and make an "F " shape. So, the angles are corresponding angles.
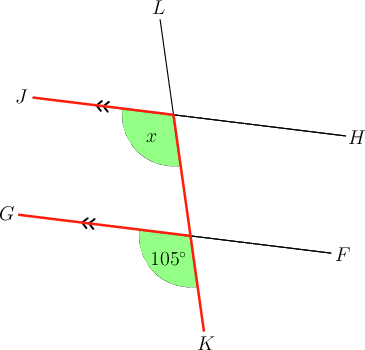
-
Step 2: Since we know that corresponding angles are equal, we can give the answer with its reason.
(corresp s; )
If you use the property of angles on parallel lines, you need to state which lines are parallel in the reason.
For Exercise 15.7, remember the facts that you have learnt about parallel lines, and decide which one of them will be useful.
Exercise 15.7: Calculate angles between parallel lines
-
In the diagram below, and is a transversal.
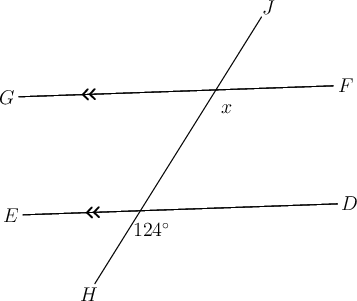
What is the value of ? (Give a reason for your answer.)
If we highlight the angles we will see an "F " shape, so these are corresponding angles.
(corresp s; )
-
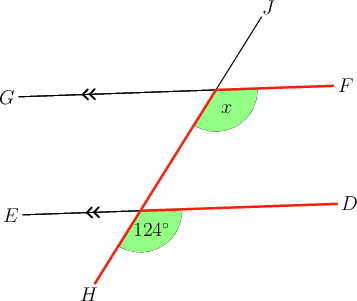
In the diagram below, and is a transversal.
What is the value of ? (Give a reason for your answer.)
If we highlight the angles we will see a "U " shape, so these are co-interior angles.

Since we know that co-interior angles add up to , we can write:
\begin{align} x + 123^{\circ} & = 180^{\circ} \quad(\text{co-int }\angle\text{s; } DE \parallel FG) \\ x & = 180^{\circ} - 123^{\circ} \\ \therefore x & = 57^{\circ} \\ \end{align} -
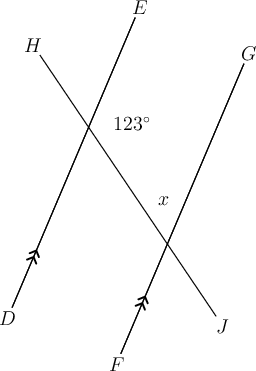
In the diagram below, and is a transversal.
Determine the size of , giving a reason for your answer.
If we highlight the angles we will see an "N " shape, so these are alternate angles.
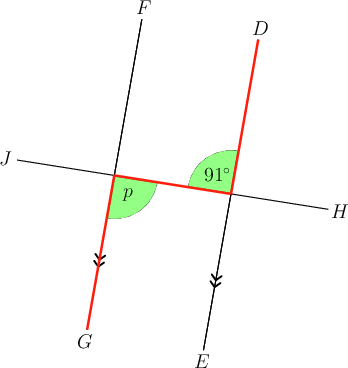
(alt ; )
-
In the diagram below, . Determine the size of , giving a reason for your answer.
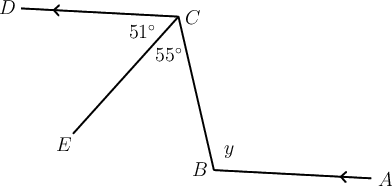
If we highlight the angles we will see an "N " shape, so these are alternate angles.
\begin{align} y & = 55^{\circ} + 51^{\circ} \quad(\text{alt }\angle\text{s; } AB \parallel CD) \\ \therefore y & = 106^{\circ} \\ \end{align}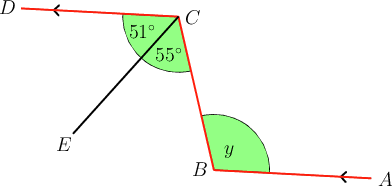
-
In the diagram below, . Determine the size of , giving a reason for your answer.
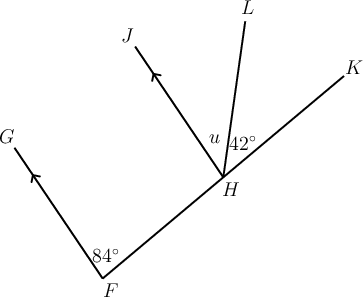
If we highlight the angles we will see an "F " shape, so these are corresponding angles.
\begin{align} u + 42^{\circ} & = 84^{\circ} \quad(\text{corresp }\angle\text{s; } FG \parallel HJ) \\ u & = 84^{\circ} - 42^{\circ} \\ \therefore u & = 42^{\circ} \\ \end{align}
Parallel lines with more than one transversal
It is possible that two parallel lines can have more than one transversal. If this is the case, it is important to identify which lines are parallel lines.
Worked example 15.13: Finding angles when there are two transversals
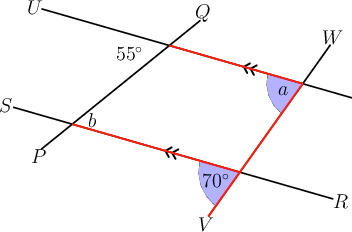
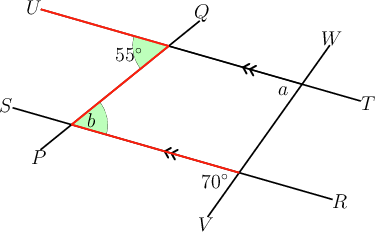
In the diagram below, . Determine the sizes of and , giving reasons for your answers.
Take note that transversal is not parallel to transversal .
-
Step 1: Remember the facts that you have learnt about parallel lines and decide if one of them will be useful here.
Corresponding angles on parallel lines are equal.
Alternate angles on parallel lines are equal.
Co-interior angles on parallel lines add up to .
-
Step 2: Concentrate on first.
We are told in the question that . We can see that the angle marked is corresponding to the angle of .
-
Step 3: Use the corresponding angles.
We know that corresponding angles on parallel lines are equal, so we can write:
\begin{align} a & = 70^{\circ}\quad\left( \text{corresp }\angle\text{s; }RS \parallel TU \right) \\ \end{align}You might have thought that was equal to . The angle of and the angle marked are corresponding angles on and . But, because and are not parallel, is not equal to .
-
Step 4: Determine the size of .
We are told in the question that . We can see that the angle marked is alternate to the angle of .
We know that alternate angles on parallel lines are equal, so we can write:
You might have thought that was equal to . The angle of and the angle marked are alternate angles on and . But, because and are not parallel, is not equal to .
Identify the parallel lines and draw over them in a different colour, if you can.
Exercise 15.8: Find angle sizes where there are two transversals
-
In the diagram below, ; is a transversal and is a transversal. Determine the sizes of and , giving reasons for your answers.

Concentrate on first.
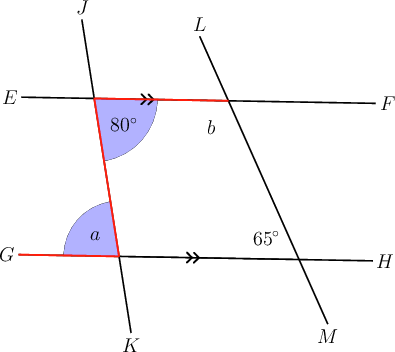
, and is alternate to the angle marked .
( is not equal to , because and are not parallel.)
Now determine the size of .
, and and the angle marked are co-interior angles.
\begin{align} b + 65^{\circ} & = 180^{\circ} \left( \text{co-int }\angle\text{s; }EF \parallel GH \right) \\ b & = 180^{\circ} - 65^{\circ} \\ b & = 115^{\circ} \\ \end{align}
(Because and are not parallel, is not equal to .)
-
In the diagram below, ; is a transversal and is a transversal. Determine the sizes of and , giving reasons for your answers.
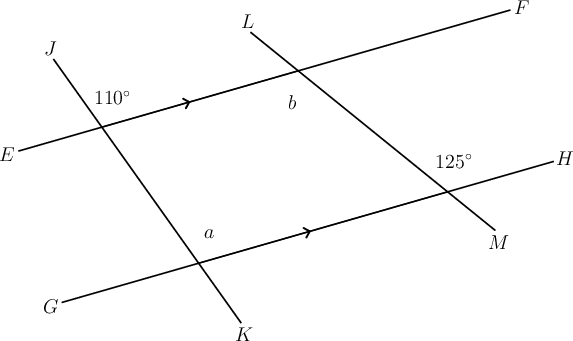
Concentrate on first.
, and is corresponding to the angle marked .
\begin{align} a & = 110^{\circ} \quad\left( \text{corresp }\angle\text{s; }EF \parallel GH \right) \\ \end{align}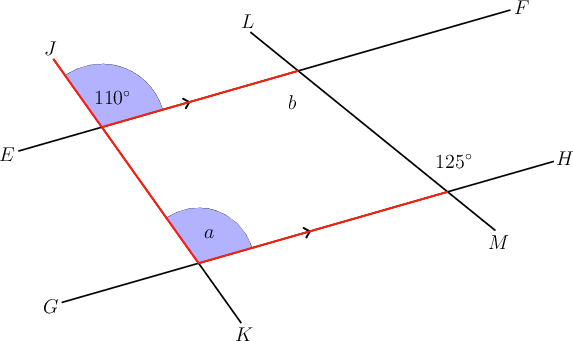
(Because and are not parallel, is not equal to .)
Now determine the size of .
, and is alternate to the angle marked .
(Because and are not parallel, is not equal to .)
-
Use adjacent, corresponding, co-interior and alternate angles to calculate the sizes of all the angles labelled with variables in the diagram. Give reasons for your answers.

You can redraw the diagram and fill in the angles as you find them.
\begin{array}{rll} a & = 180° - 42° = 138° & \text{(}\angle \text{s on str line)} \\ b & = 42° & \text{(vert opp } \angle\text{s }\text{)}\\ c & = 138° & \text{(vert opp } \angle\text{s }\text{)}\\ d & = 138° & \text{(alt }\angle\text{s; } AB \parallel CD \text{)}\\ e & = 180° - 138° = 42° & \text{(}\angle \text{s on str line)}\\ f & = 138° & \text{(vert opp } \angle\text{s }\text{)}\\ g & = 42° & \text{(vert opp } \angle\text{s }\text{)} \end{array}
When we determine the angles formed by two parallel lines and a transversal, we sometimes need more than one step to find the solution to the question. The worked example below shows how to do this.
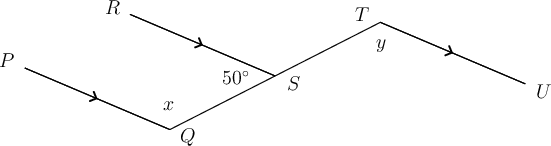
Worked example 15.14: Solving two-step problems with parallel lines
In the diagram below, and is a transversal. Determine the value of . Give reasons for all your statements.
-
Step 1: Consider the diagram and plan how you will get to the answer.
We cannot determine the value of in just one step. It is a good idea to begin with the angle that is given.
-
Step 2: Choose another angle that is closer to and has a relationship to the angle you need to find.
so we can use the F-U-N angles. We can see that is alternate to the angle.
-
Step 3: Find the size of the other angle.
\begin{align} K\hat{R}S & = 65^{\circ} \quad(\text{alt }\angle\text{s; }JK \parallel LM) \\ \end{align}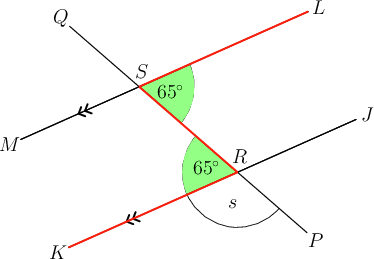
-
Step 4: Determine the value of .
Now that we know the size of , we can determine .
We can see that and are angles on a straight line.
\begin{align} s + 65^{\circ} & = 180^{\circ} \quad(\text{adj }\angle\text{s on str line}) \\ s & = 180^{\circ} - 65^{\circ} \\ \therefore s & = 115^{\circ} \\ \end{align}
Exercise 15.9: Solve two-step problems with parallel lines
-
In the diagram below, and is a transversal.
Determine the value of . Give a reason for each statement.
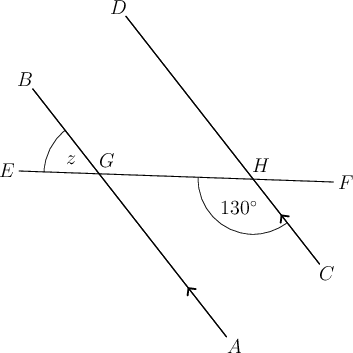
There is more than one way to answer this question. One possible answer is given here.
We cannot determine the size of in just one step. So, we must use the angle of to get us closer to the angle marked . Then we will be able to work out .
We can see that and the angle are corresponding angles.
\begin{align} A\hat{G}E & = 130^{\circ} \quad(\text{corresp }\angle\text{s; } AB \parallel CD) \\ \end{align}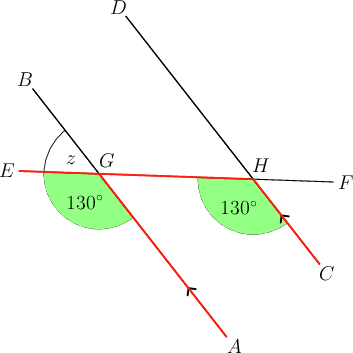
Now that we know the size of , we can determine .
We can see that forms a straight line with .

We already know that , so we can write:
\begin{align} z + 130^{\circ} & = 180^{\circ} \quad(\text{adj }\angle\text{ s on str line}) \\ \therefore z & = 180^{\circ} - 130^{\circ} \\ \therefore z & = 50^{\circ} \\ \end{align} -
In the diagram below and is a transversal.
Determine the value of . Give a reason for each statement.
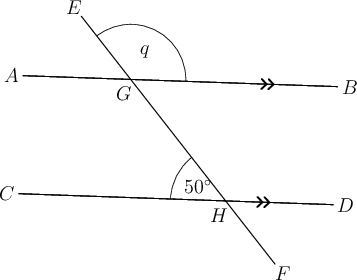
There is more than one way to answer this question. One possible answer is given here.
Use the angle of to get us closer to the angle marked .
We can see that and the angle of are corresponding angles.
\begin{align} A\hat{G}E & = 50^{\circ} \quad(\text{corresp }\angle\text{s; } AB \parallel CD) \\ \end{align}
We can see that the angle marked forms a straight line with .
\begin{align} q + 50^{\circ} & = 180^{\circ} \quad(\text{adj }\angle\text{s on str line}) \\ \therefore q & = 180^{\circ} - 50^{\circ} \\ \therefore q & = 130^{\circ} \\ \end{align}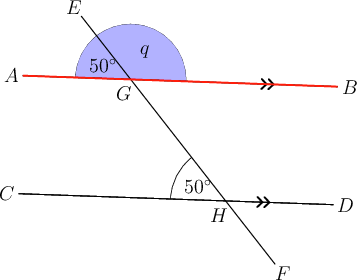
Working with more than two parallel lines
We do not have to work with two parallel lines only. Sometimes there are more than two parallel lines in a diagram. The trick is to focus on only two parallel lines at a time, and to remember the F-U-N angles. The worked example below shows how to do this.
Worked example 15.15: Finding two angles with three parallel lines
In the diagram below, . Determine the values of and , giving reasons for your answers.
Take note: There is often more than one way to answer a geometry question. One possible solution is shown below.
-
Step 1: Remember the facts that you have learnt about parallel lines and decide if one of them will be useful here.
Corresponding angles on parallel lines are equal .
Alternate angles on parallel lines are equal.
Co-interior angles on parallel lines add up to .
-
Step 2: Concentrate on first.
We can see that the angle marked and the angle of are co-interior angles between the parallel lines and .
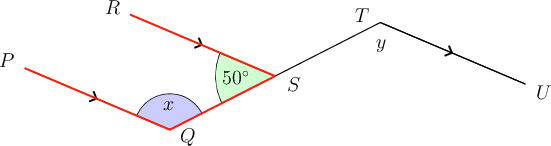
-
Step 3: Determine the value of .
\begin{align} x + 50^{\circ} & = 180^{\circ}\,(\text{co-int }\angle\text{s; }PQ \parallel RS) \\ \therefore x & = 180^{\circ} - 50^{\circ} \\ \therefore x & = 130^{\circ} \\ \end{align} -
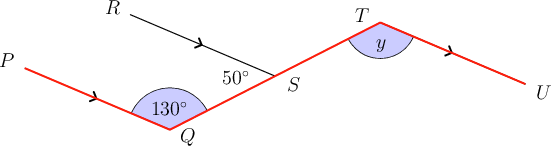
Step 4: Now focus on .
We already know that = . If you look carefully, you can see that the angle marked is alternate to on the parallel lines and . We now know that is .
-
Step 5: Determine the value of .
\begin{align} y & = 130^{\circ}\,(\text{alt }\angle\text{s; }PQ \parallel TU) \\ \end{align}You might have answered this question by applying adjacent angles on a straight line to get , and then alternate angles on and . This would be marked as correct in a test (if you wrote all of your reasons correctly).
Exercise 15.10: Find two angles with three parallel lines
-
In the diagram below, . Determine the values of and , giving reasons for your answers.

One possible solution is shown below.
First determine the value of .
We can see that the angle marked is alternate to the angle of angle on the parallel lines and .
\begin{align} x & = 100^{\circ}\,(\text{alt }\angle\text{s; }PQ \parallel RS) \\ \end{align}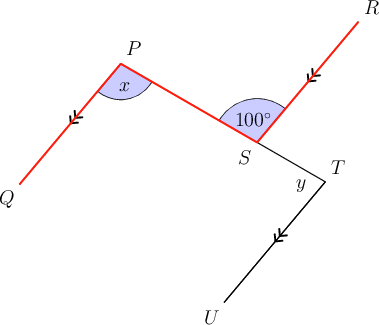
Now determine the value of .
We already know that = . If you look carefully, you can see that the angle marked and the angle of are co-interior angles on the parallel lines and .
\begin{align} y + 100^{\circ} & = 180^{\circ}\,(\text{co-int }\angle\text{s; }PQ \parallel TU) \\ \therefore y & = 180^{\circ} - 100^{\circ} \\ \therefore y & = 80^{\circ} \\ \end{align}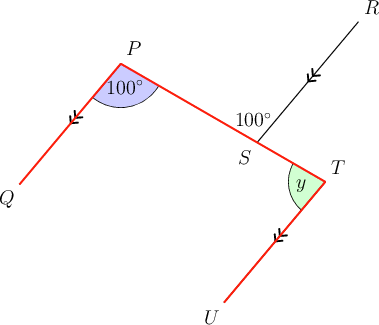
You might have answered this question by doing adjacent angles on a straight line to get and then alternate angles on and . This would be marked as correct in a test (if you wrote all of your reasons correctly).
-
In the diagram below, . Determine the values of and , giving reasons for your answers.
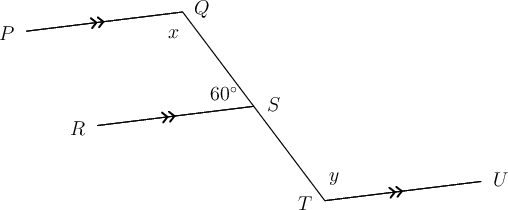
One possible solution is shown below.
First determine the size of .
We can see that the angle marked and the angle of are co-interior angles on the parallel lines and .
\begin{align} x + 60^{\circ} & = 180^{\circ}\,(\text{co-int }\angle\text{s; }PQ \parallel RS) \\ \therefore x & = 180^{\circ} - 60^{\circ} \\ \therefore x & = 120^{\circ} \\ \end{align}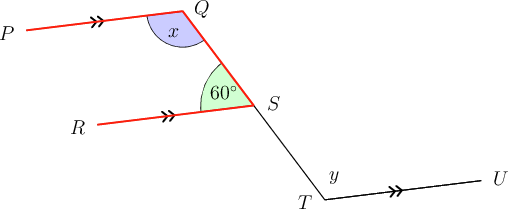
Now determine the value of .
We already know that = . If you look carefully, you can see that the angle marked is alternate to the angle of on the parallel lines and .
\begin{align} y & = 120^{\circ}\,(\text{alt }\angle\text{s; }PQ \parallel TU) \\ \end{align}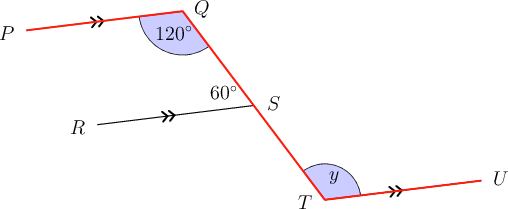
You might have answered this question by applying adjacent angles on a straight line to get , and then alternate angles on and . This would be marked as correct in a test (if you wrote all of your reasons correctly).
15.4 Practical applications
When we know about different angles and how they are formed we can apply our knowledge in real life. For example, we can use angles to describe the position of a shop, or how we want to paint decorations. Many people use angles in their jobs every day.
Worked example 15.16: Solving real-world problems with angles
Suleiman is not sure where to find a specific shoe shop in the nearby city. He has a discussion with his friend Musa who knows where many of the shops in the city are.
Musa: "Do you know remember where the cell phone shop is where I bought my cell phone? "
Suleiman: "Yes, I know exactly where that shop is. "
Musa: "Well, the shoe shop is vertically opposite the cell phone shop. "
At what number on the map will Suleiman find the shoe shop if the cell phone shop is at number 1 on the map?
-
Step 1: Consider the diagram and interpret the diagram.
The middle of the intersection is the common point between the streets. The two streets are intersecting lines, so they form vertically opposite angles.
-
Step 2: Read the question carefully and find the cell phone shop.
The cell phone shop is at number 1 on the map.
-
Step 3: Identify the angle that is vertically opposite angle number 1 on the map.
Shop number 1 and shop number 3 are at vertically opposite angles of the point of intersection.
-
Step 4: Give the answer.
The shoe shop is at number 3 on the map.
Exercise 15.11: Solve real-world problems with angles
-
Tinuke wants to buy clothes and is not sure where to find a a good clothing shop in her town. She asks her friend Kemi for help.
Kemi: "Do you know remember where the hairdresser is where I went for a haircut? "
Tinuke: "Oh, yes, I do remember that hairdresser. "
Kemi: "Vertically opposite the hairdresser there is a good clothing shop. "
At what number on the map will Tinuke find the clothing shop if the hairdresser is at number 2 on the map?

The two streets are intersecting lines so they form vertically opposite angles.
The hairdresser is at number 2 on the map.
Shop number 2 and shop number 4 are vertically opposite angles, so the clothing shop is at number 4 on the map.
-
Adanna wants to paint "NIGERIA " in big letters on a wall. She starts out with the "N " and paints the first two lines of the letter. Adanna still needs to paint the third line of the letter "N ".

How can Adanna find the size of the angle that she must form when she begins to paint the third line of the letter "N "? Give a reason for your answer.
The two vertical lines of a capital letter "N " are parallel. This means that the two marked angles in the diagram below should be equal.

Use a protractor to measure the angle that is completed already. The acute angle is equal to .

Answer: The angle between the second and third line of the letter "N " should also be . The reason for this is that the first and third lines of the letter "N " are parallel, so the alternate angles are equal.

-
Babatunde and his brother earn income by doing welding jobs. They use their knowledge of angles and lines often in their work. The photo below shows the rails in front of a house that they designed and made.

-
What is the relationship between the bottom rail (marked ) and the balusters (marked and )?
is perpendicular to and is also perpendicular to .
-
What is the relationship between the balusters marked and ?
and are parallel.
-
What should the size of the angle marked be if is equal to ?
and are parallel lines and is a transversal.
and are corresponding angles, which means they are equal. Therefore, =
and are on a straight line, so they add up to . is .
\begin{align} x + 120^{\circ} & = 180^{\circ} \\ \therefore x & = 60^{\circ} \end{align}The size of the angle marked is .
-
15.5 Summary
- An angle is the amount of turn between two straight lines that have a common end point, called the vertex of the angle.
- We use a protractor to measure angles in degrees. Always estimate an angle before you measure it, so you can check whether your answer seems correct.
- Different types of angles have different names. Those used in this chapter are provided in the table.
| Name of angle | Size of angle |
|---|---|
| acute angle | between and |
| right angle | |
| obtuse angle | between and |
| straight angle | |
| reflex angle | between and |
| revolution |
- A straight line is also called a straight angle. A straight angle is equal to .
- If a straight line is formed by more than one angle, the sum of those angles will be . We say the angles are supplementary angles.
- Adjacent angles are next to each other. Two adjacent angles share the same vertex and one common arm.
- When two lines cross each other, we say they are intersecting lines.
- Two intersecting straight lines form vertically opposite angles, which have the same vertex and are on opposite sides of the vertex. Vertically opposite angles are equal.
- Parallel lines are always the same distance apart, and are indicated using arrow symbols.
- A transversal intersects two or more parallel lines.
- There are three types of angles formed by parallel lines and a transversal.
- Corresponding angles are in matching positions on the parallel lines and the transversal, and make "F " shape. Corresponding angles on parallel lines are equal.
- Co-interior angles are inside the parallel lines and on the same side of the transversal. They make a "U " shape. Co-interior angles on parallel lines are supplementary (add up to ).
- Alternate angles are inside the parallel lines, but on different sides of the transversal. They make an "N " shape. Alternate angles on parallel lines are equal.