Chapter 10: Simplifying algebraic expressions
So far we have dealt with open sentences that involve using a symbol or a variable (a letter that represents a number) and contain an equals sign. This is part of a topic in mathematics we call algebra. In this chapter we will be dealing with algebraic expressions and how to simplify them.
10.1 Algebraic expressions and terms
Open sentences are made up of algebraic expressions. An algebraic expression is a mathematical phrase or statement that contains numbers, symbols, variables (such as or ) and operators (such as , , and ). Note that algebraic expressions do not have equals signs.
Here are some examples of algebraic expressions:
algebraic expression An algebraic expression is a mathematical statement that contains a combination of numbers, symbols, variables and mathematical operators. It does not have an equals sign.
Algebraic expressions are made up of terms that are separated by an addition ( ) or a subtraction sign.
The algebraic expression has two terms.
has 3 terms.
has 4 terms.
term A term can be a single number (positive or negative), or a variable, or one or more numbers and variables that are being multiplied together. Terms are separated by or signs.
Here are some examples of single terms:
Here are some examples of algebraic expressions with two terms:
Here are some examples of algebraic expressions with five terms:
Worked example 10.1: Determining number of terms
How many terms does the following algebraic expression have?
-
Step 1: Remember what a term is.
Terms are separated by an addition or subtraction sign.
-
Step 2: Identify the and signs in the expression.
You may circle the the or signs to help you:
-
Step 3: Count the number of terms on either side of the and signs.
The expression has three terms.
Exercise 10.1: Determine the number of terms in an algebraic expression
How many terms do each of the following algebraic expressions contain?
-
2 terms
-
3 terms
-
1 term
-
1 term
-
3 terms
-
2 terms
-
2 terms
-
1 term
-
1 term
-
3 terms
10.2 Working with algebraic expressions
When you learnt to add or subtract objects you learnt that, for example:
- 1 apple + 1 apple + 1 apple + 1 apple can be written as 4 apples
When you started working with multiplication you learnt that, for example:
-
1 apple + 1 apple + 1 apple + 1 apple can be written as 4 (1 apple) = 4 apples
-
2 apples + 2 apples + 2 apples can be written as 3 (2 apples) = 6 apples
-
9 + 9 + 9 + 9 can also be written as 4 9
-
3 + 3 + 3 + 3 + 3 + 3 + 3 can also be written as 7 3
The same principles apply in algebra. But remember that in algebra, we use a letter or variable to replace a number. For example:
In algebra, we normally do not write the multiplication sign between a number and a variable. For example, we write as .
Here are a few more examples:
Worked example 10.2: Writing algebraic expressions
Write the following expression using a simpler notation:
-
Step 1: Check what operations are being used.
In this case, only addition is used.
-
Step 2: Count the number of s.
There are 5 s.
-
Step 3: Write the algebraic expression in a simpler notation.
Exercise 10.2: Simplify expressions
Write the following expressions in a simpler notation:
-
-
or 21
-
-
-
-
or
-
-
-
or
-
or
Constants and coefficients
There are two other words you also need to know and understand when working with algebraic terms: constant and coefficient.
The following algebraic expression contains two terms:
5 is called a constant term as the value will always be 5 and it will not vary. The value of the term will vary depending on the value of the variable . In the term, the is called the variable and the is called the coefficient.
constant A constant is a term without a variable. A constant can have a negative value (if it has a minus sign in front of it) or a positive value (if it has a plus sign or no sign in front of it).
coefficient The coefficient is the number (factor) being multiplied by the variable. A coefficient can have a negative value (if it has a minus sign in front of it) or a positive value (if it has a plus sign or no sign in front of it).
Here are some more examples of terms that will vary in value, depending on the value of the variable:
In , the 3 is the coefficient of . We know there are three s.
-
If , then .
-
If , then .
In , the 2 is the coefficient of . We know there are two s.
-
If , then .
-
If , then .
In , the 5 is the coefficient of . We know there are five s.
-
If , then
-
If , then
In , the coefficient of is 1. We know there is only one .
-
If , then .
-
If , then .
The terminology we use in algebra that we have learnt so far are summarised here:

Worked example 10.3: Identifying the different parts of an algebraic expression
For the algebraic expression below, write down the number of terms, the constant term, the coefficient of , the coefficient of and the coefficient of .
-
Step 1: Identify and count the number of terms.
There are 4 terms.
-
Step 2: The constant is the term that doesn't have a variable. The plus or minus sign in front of the term is part of the constant.
6 is the constant.
-
Step 3: To find the coefficient of , look for the term that contains an . The plus or minus sign in front of the term is part of the coefficient.
In algebra, we normally do not write down the plus sign in front of the very first term.
The coefficient of is 2 or 2.
-
Step 4: To find the coefficient of , look for the term that contains a . The plus or minus sign in front of the term is part of the coefficient.
In algebra, we normally do not write down the number 1 if it is the coefficient of a variable.
The coefficient of is 1 or 1.
-
Step 5: To find the coefficient of , look for the term that contains a . The plus or minus sign in front of the term is part of the coefficient.
The coefficient of is 4.
Exercise 10.3: Identify parts of an algebraic expression
-
How many terms does this expression contain?
2
-
What is the constant in this algebraic expression?
3
-
What is the coefficient of this term?
8
- Answer the questions about this expression:
.
a) How many terms does this expression have?
b) What is the coefficient of ?
c) What is the coefficient of ?
d) What is the value of the constant term?
a) 3
b) 21 or 3 7
c) 5
d) 1
- Answer the questions about this expression:
.
a) How many terms does this expression have?
b) What is the coefficient of ?
c) What is the coefficient of ?
d) What is the value of the constant term?
a) 4
b) 1
c) 1
d) 10
10.3 Adding and subtracting like terms
We have seen that we can add to get .
These three terms are called like terms because they all contain the same variable, .
We can also add . Because both terms have the variable , we can combine the terms using the operation that is given, which in this case is addition. The correct answer is:
\[\begin{array}{l}
{3x + 4x = 7x}
\end{array}\]
We can also subtract like terms. We can simplify the expression \(\; 10a - 2a\) using subtraction. The correct answer is:
\[\begin{array}{l}
{10a - 2a = 8a}
\end{array}\]
When we collect or combine the like terms in this way, we are giving an expression in its simplest form, which is called simplifying an expression.
like terms Like terms contain the same variable or variables.
simplify an expression To simplify an expression is to give it in its simplest form. We do this by collecting (combining) like terms using addition or subtraction.
We can add or subtract any number of like terms.
For example:
Terms that do not have the same variables are called unlike terms. If we find an expression with unlike terms, we cannot add or subtract these terms. For example: contains two unlike terms. They have the same coefficient but not the same variable. This expression cannot be simplified further.
unlike terms Unlike terms contain different variables.
Exercise 10.4: Add and subtract like terms
Simplify the following expressions.
-
-
-
or
-
(There are no like terms.) -
-
-
-
-
(There are no like terms.) -
(There are no like terms.)
Sometimes expressions contain both like terms and unlike terms. To simplify an expression like this, we collect the like terms. This means we rearrange the terms first to group all the like terms together. Then we add or subtract the like terms to simplify the expression.
Worked example 10.4: Collecting like terms to simplify an expression
Simplify the expression by collecting the like terms.
-
Step 1: Rearrange the terms so that you group all the like terms together.
-
Step 2: Add or subtract the like terms and give the simplified expression.
Worked example 10.5: Collecting like terms to simplify an expression
Simplify the expression by collecting the like terms.
-
Step 1: Rearrange the terms so that you group all the like terms together. Keep the sign in front of each term with that term.
-
Step 2: Add or subtract the like terms and give the simplified expression. Pay special attention to the signs of the coefficients.
Go back to Chapter 5 to revise how to add and subtract positive and negative numbers.
Worked example 10.6: Collecting like terms to simplify an expression
Simplify the expression by collecting the like terms.
-
Step 1: Rearrange the terms so that you group all the like terms together. Keep the sign in front of each term with that term.
When there are constants in an expression, treat them as like terms.
-
Step 2: Add or subtract the like terms and give the simplified expression. Pay special attention to the signs of the coefficients.
Exercise 10.5: Simplify by collecting like terms
Simplify the following expressions by collecting like terms.
-
\begin{align} &= 2h + 3h + 5m + 2m + m \\ &= 5h + 8m \end{align}
-
\begin{align} &= 18p - 16p - 2x - x \\ &= 2p - 3x \end{align}
-
\begin{align} &= 9x - 10x - 3y - 2y +y \\ &= -x -4y \end{align}
-
\begin{align} &= 13x - 6x - x +2y +7y \\ &= 6x + 9y \end{align}
-
\begin{align} &= -2a - 6a - 20b +b \\ &= -8a-19b \end{align}
-
\begin{align} &= 2 + 9 + 8k - k \\ &= 11 +7k \end{align}
-
\begin{align} &= 28 - 16 - 4m - 28m \\ &= 9 - 32m \end{align}
-
\begin{align} &= -7x + 7x + 7y - 7y \\ &= 0 \end{align}
-
\begin{align} &= 11a - 4a + 11b - 2b + 11c + c \\ &= 7a + 9b + 12c \end{align}
-
\begin{align} &= 3x - 5x - 2y - 2 - 4 \\ &= -2x - 2y - 6 \end{align}
10.4 Working with brackets in algebraic expressions
We sometimes use brackets to group terms in algebraic expressions together.
As you know, means .
If we replace the with , then in the same way:
We can use repeated addition to work out any multiplication, so:
We need to remove the brackets before we can collect the like terms and simplify the expression:
Therefore:
\begin{align} &\phantom{000}2 \times (x + y) \\ &= (x + y) + (x + y) \\ &= x + y + x + y \\ &= x + x + y + y \\ &= 2x + 2y \end{align}Worked example 10.7: Removing brackets using repeated addition
. Replace the with . Then remove the brackets and simplify the expression.
-
Step 1: Replace the with .
-
Step 2: Use repeated addition to work out this multiplication.
\begin{align} &\phantom{000}4 \times (a + b) \\ &= (a+b) + (a+b) + (a+b) + (a+b) \\ \end{align} -
Step 3: Remove the brackets.
\begin{align} &\phantom{000}4 \times (a + b) \\ &= (a+b) + (a+b) + (a+b) + (a+b) \\ &= a + b + a + b + a + b + a + b \\ \end{align} -
Step 4: Collect the like terms and simplify.
\begin{align} &\phantom{000}4 \times (a + b) \\ &= (a+b) + (a+b) + (a+b) + (a+b) \\ &= a + b + a + b + a + b + a + b \\ &= a + a + a + a + b + b + b + b \\ &= 4a + 4b \end{align}
Exercise 10.6: Remove brackets and simplify
Remove the brackets using repeated addition and then simplify.
-
\begin{align} &= 2 \times (h+m) \\ &=(h + m) + (h + m) \\ &= h+m+h+m \\ &= h + h + m + m \\ &=2h + 2m \end{align}
-
\begin{align} &= 3 \times (p+k) \\ &=(p + k) + (p + k) + (p + k) \\ &=p+k+p+k+p+k \\ &= p + p + p + k + k + k \\ &=3p + 3k \end{align}
-
\begin{align} &= 2 \times (a+2) \\ &=(a + 2) + (a + 2) \\ &=a+2+a+2 \\ &= a + a + 2+ 2 \\ &=2a + 4 \end{align}
-
\begin{align} &= 3 \times (4x+3y) \\ &=(4x + 3y) + (4x + 3y) + (4x + 3y) \\ &=4x+3y+4x+3y+4x+3y \\ &= 4x + 4x + 4x + 3y + 3y + 3y \\ &=12x + 9y \end{align}
-
\begin{align} &= 2 \times (10a - 6b + c) \\ &=(10a - 6b + c) + (10a - 6b + c) \\ &=10a - 6b + c + 10a - 6b + c \\ &= 10a + 10a - 6b - 6b + c + c \\ &=20a - 12b + 2c \end{align}
Negative signs before brackets
Up to now we only worked with brackets that have a positive sign in front of them. When there is a negative sign before a bracket, it affects all the terms inside the bracket.
Look at this example:
We can simplify it as follows:
\begin{align} &\phantom{000}10-(2+3) \\ &=10-5 \\ &=5 \end{align}This is the same as:
\begin{align} &\phantom{000}10-(2+3) \\ &=10-2-3 \\ &=8-3 \\ &=5 \end{align}It is NOT the same as:
So, if we remove a bracket with a negative sign in front of it, we change the signs of all the terms inside the bracket. Here are some examples:
Worked example 10.8: Removing brackets with negative signs in front
Remove the brackets and then simplify the following expression:
-
Step 1: Use repeated addition to work out multiplication of brackets.
\begin{align} &\phantom{000}2(4m + n)-(5m+3n) \\ &= (4m+n) + (4m+n) - (5m+3n) \\ \end{align} -
Step 2: Remove the brackets. If there is a negative sign in front of a bracket, change the signs of all the terms inside the bracket.
\begin{align} &\phantom{000}2(4m + n)-(5m+3n) \\ &= (4m+n) + (4m+n) - (5m+3n) \\ &=4m+n+4m+n-5m-3n \\ \end{align} -
Step 3: Collect the like terms and simplify.
\begin{align} &\phantom{000}2(4m + n)-(5m+3n) \\ &= (4m+n) + (4m+n) - (5m+3n) \\ &=4m+n+4m+n-5m-3n \\ &=4m+4m-5m+n+n-3n \\ &=3m-n \end{align}
Exercise 10.7: Remove brackets with negative signs and simplify
Remove the brackets and then simplify.
-
\begin{align} &= 3k-2p-k \\ &=3k-k-2p \\ &=2k-2p \end{align}
-
\begin{align} &= 2h +m-m-2h-m \\ &=2h-2h+m-m-m \\ &=0-m \\ &=-m \end{align}
-
\begin{align} &=-4x - 3y + 2x -y \\ &=-4x+2x-3y-y \\ &=-2x-4y \end{align}
-
\begin{align} &=(a + 2) + (a + 2) +(a+2) -(4a+2) \\ &=a+2+a+2+a+2-4a-2 \\ &=a + a + a-4a +2+ 2+2-2 \\ &=-a + 4 \end{align}
-
\begin{align} &=(10a - 6b + c) + (10a - 6b + c) -(3c-2b-a)-(b+c) \\ &=10a - 6b + c + 10a - 6b + c -3c+2b+a-b-c \\ &=10a + 10a +a - 6b - 6b +2b -b + c + c -3c-c \\ &=21a - 10b - 2c \end{align}
When we change the signs of the terms inside a bracket that has a negative sign in front of it, we actually multiply each term by 1. You will learn more about this next year.
10.5 Working with brackets using the distributive law
When we have an expression with brackets, we know we need to multiply. When we do the multiplication, we say that we expand the expression.
From the examples and the exercises above, can you see a shorter way than repeated addition to multiply the expressions? The simpler way is to multiply the coefficient of the bracket by each of the terms that is inside the bracket.
When we do this, we are applying the distributive law. This law states that:
In other words, 4 groups of is the same as 4 groups of 3 plus 4 groups of 2. So the can be "distributed" across the , to get:
By now you know that .
Note that the bracket is seen as one "package" that can be replaced by one variable. Therefore, the expression has one term, but the expression has two terms.
expand To expand an algebraic expression is to multiply what is outside the brackets (the coefficient of the bracket) by each of the terms that is inside the bracket.
distributive law The distributive law states that the multiplying factor (the coefficient) can be distributed across each of the terms inside a bracket, so .
Worked example 10.9: Multiplying the coefficient of a bracket by two terms inside
Expand this expression:
-
Step 1: Multiply the 3 by the first term in the bracket, which is .
Remember that means .
So the first term is
-
Step 2: Multiply the 3 by the second term in the bracket, which is .
The second term is .
-
Step 3: Write the new terms of the expression with the correct operator, which in this case is .
Worked example 10.10: Multiplying the coefficient of a bracket by three terms inside
Expand the expression .
-
Step 1: Multiply the 2 by the first term in the bracket.
-
Step 2: Multiply the 2 by the second term in the bracket.
-
Step 3: Multiply the 2 by the third term in the bracket.
-
Step 4: Write the new terms of the expression with the correct operation signs.
When you expand, you do not need to write all the steps separately as shown in the worked examples above. You can go directly to the answer by writing each new term as you work it out. So your answer could look like this:
Exercise 10.8: Use the distributive law to expand and simplify expressions
Use the distributive law to expand the brackets and then simplify the expressions.
-
-
\begin{align} &=10n-80-5m+4m \\ &=10n-80-m \end{align}
-
\begin{align} &=6x-6y+6+3x-3y+3 \\ &=6x+3x-6y-3y+6+3 \\ &=9x-9y+9 \end{align}
-
\begin{align} &=15x-20y+5z+3x+3y-6z \\ &=15x+3x-20y+3y+5z-6z \\ &=18x-17y-z \end{align}
-
\begin{align} &=36a+33b+33c-2a+b-c \\ &=36a-2a+33b+b+33c-c \\ &=34a+34b+32c \end{align}
Order of operations
In Chapter 9 you were reminded of the correct order of operations that you learnt last year:
- Brackets
- Of
- Divide
- Multiply
- Add
- Subtract
Worked example 10.11: Following the correct order of operations
Simplify the expression .
-
Step 1: Simplify the terms inside the bracket first.
-
Step 2: There is no "of" or division in the expression, so do multiplication next.
Use the distributive law to multiply the bracket by its coefficient.
Remember that means .
-
Step 3: Collect the like terms and simplify.
\begin{align} &\space 16x+2+12x \\ =&\space 16x+12x+2 \\ =&\space 28x+2 \end{align}
Worked example 10.12: Following the correct order of operations
Simplify the expression .
-
Step 1: Simplify the terms inside the brackets first.
-
Step 2: There is no "of" in the expression, so do division next.
When we multiply a term that has a variable by a number, we simply multiply the coefficient of the term by the number. For example . In the same way, when we divide a term that has a variable by a number, we simply divide the coefficient of the term by the number. For example
-
Step 3: Multiplication comes after division.
-
Step 4: Addition comes after multiplication.
-
Step 5: Do subtraction last.
Exercise 10.9: Follow the correct order of operations to simplify expressions
Simplify the expressions.
-
\begin{align} &=5y-y \\ &=4y \end{align}
-
\begin{align} &=4x(5)-x-2 \\ &=20x-x-2 \\ &=19x-2 \end{align}
-
\begin{align} &=x(2+12)-x-2x \\ &=x(14)-x-2x \\ &=14x-x-2x \\ &=11x \end{align}
-
\begin{align} &=4x\times 2+3x \times 3 \\ &=8x+9x \\ &=17x \\ \end{align}
-
\begin{align} &=2(x+y)-(2x-3x+y) \\ &=2(x+y)-(x+y) \\ &=2x+2y-x-y \\ &=2x-x+2y-y \\ &=x+y \end{align}
-
\begin{align} &=5y-(4y-4)+6y \\ &=5y-4y+4+6y \\ &=5y-4y+6y+4 \\ &=11y-4y+4 \\ &=7y+4 \end{align}
-
\begin{align} &=-p-q-p+q+2p-2q \\ &=-p-p+2p-q+q-2q \\ &=0-2q \\ &=-2q \end{align}
-
\begin{align} &=-3m(-5+5)+2m\times3 \\ &=-3m(0)+6m \\ &=0+6m \\ &=6m \end{align}
-
\begin{align} &=4x+8x+2 \\ &=12x+2 \end{align}
-
\begin{align} &=3(-2a+4a+b-2b+c+c)-(a-b-c) \\ &=3(2a-b+2c)-(a-b-c) \\ &=6a-3b+6c-a+b+c \\ &=6a-a-3b+b+6c+c \\ &=5a-2b+7c \end{align}
10.6 Practical applications
Using area to show the distributive law in practice
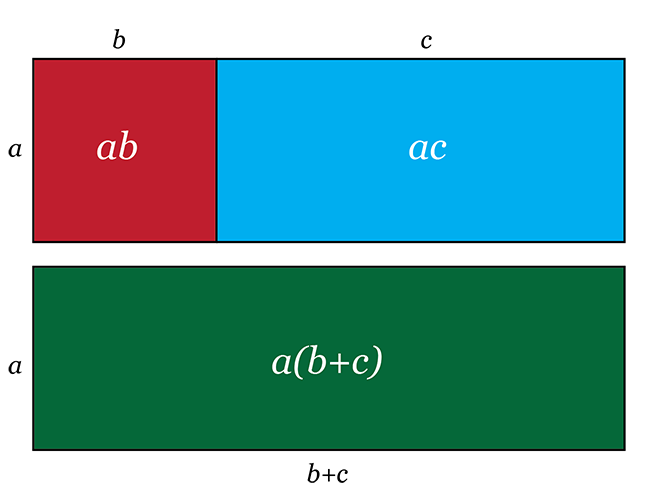
We can use areas to show the distributive law in practice. For example, look at the two rectangles shown below. There are two ways in which we can write the total area of the two rectangles.

Method 1: Calculate the area of each rectangle separately, and then add the areas.
-
Area of smaller rectangle: square units
-
Area of larger rectangle: square units
-
Total area of the two rectangles:
\begin{align} A&=(3 \times 2) + (3 \times 4) \\ &=6+12 \\ &=18 \text{ square units} \end{align}
Method 2: Calculate the total area of the combined rectangle.
-
Width of total rectangle:
-
Length of total rectangle:
-
Total area of the two rectangles:
\begin{align} A&=3 \times (2 + 4) \\ &=3 \times 6 \\ &=18 \text{ square units} \end{align}
From this practical example we can see that:
Exercise 10.10: Use algebraic expressions to show the distributive law in practice
-
Write down two different expressions for the total area of the two rectangles shown below. Draw sketches to show your working, and use the variables in terms of and in your expressions.
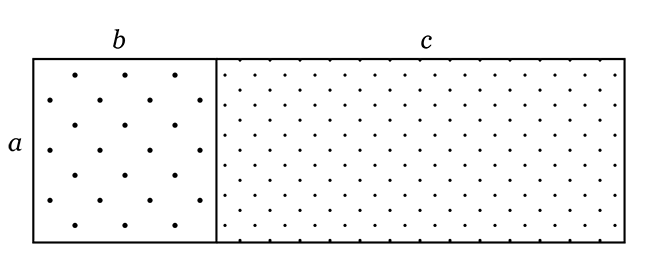
or
-
Write down the total area of the rectangles given below in two different ways.
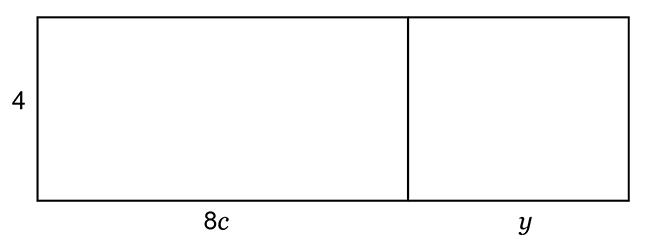
or
Using algebraic expressions to solve everyday problems
Algebraic expressions can be very useful when you need to solve everyday problems. It allows us to use variables as representations of numbers where the value may vary.
Suppose you get ₦500 pocket money every month and you want to keep track of what is happening to your money. You spend your pocket money on sweets, transport and data for your mobile. You can set up an expression to represent this:
\[\text{money available}=₦\,500-(s+t+d)=₦\,500-s-t-d\]At any time during the month, you can put the amounts of money you spent on each item into your expression. This will give you the amount of money you have left for the rest of the month.
Algebraic expressions can also be used to solve mathematical problems. Here are some tips that you may find useful:
- Three consecutive numbers can be represented as:
- More than, for example 5 more than :
- Less than, for example 5 less than :
- Double or twice, for example double or twice :
- Half, for example half of : or
- Seconds in minutes and hours: and
- Kobo in naira:
- Total cost, for example total cost of and :
- Area of a rectangle:
- Perimeter of a rectangle:
Exercise 10.11: Use algebraic expressions for practical problems
-
A father is years old. His daughter is currently half his age. How old will his daughter be in 10 years' time?
The age of the daughter will be , where is the current age of the father.
-
A long-distance athlete covers an average distance of per minute. How far does she run in ?
In , the athlete runs .
-
A shop owner sells maize at \(₦\,x\) per cup. She also sells rice per cup, at double the price of the maize. If she sold 50 cups of maize and 45 cups of rice, what was her income?
The price of her rice is \(₦\,2x\) per cup.
\begin{align} &\phantom{000}50\times x+45\times 2x \\ &=50x+90x \\ &=140x \end{align}Her income is \(₦\,140x\), where \(₦\,x\) is the price of one cup of maize.
-
A small sachet of milk costs \(₦\,x\) and a small sachet of noodles costs \(₦\,20\) more. Work out the cost of 4 sachets of milk and 8 sachets of noodles.
A small sachet of noodles costs \(₦\,x+20\).
\begin{align} &\phantom{000}4\times x+8\times (x+20) \\ &=4x+8(x+20) \\ &=4x+8x+160 \\ &=12x+160 \end{align}The cost is \(₦\,12x+160\), where \(₦\,x\) is the price of a small sachet of milk.
-
The length of a rectangle is 3Â cm more than its breadth. Calculate the perimeter of the rectangle.
\begin{align} P&=2l+2b \\ &=2(b+3)+2b \\ &=2b+6+2b \\ &=4b+6 \end{align}
The perimeter is , where is the breadth.
-
The sum of three consecutive numbers is . If the first of the three numbers is , determine .
The numbers are , and .
\begin{align} y&=a+(a+1)+(a+2) \\ &=a+a+1+a+2 \\ &=a+a+a+1+2 \\ &=3a+3 \end{align}, where is the first number.
-
In a Mathematics test, Safiyah scored marks. Nkechi scored 7 marks more than Safiyah. Fadekemi scored 4 marks less than Nkechi. Work out the total mark of the three girls together.
Safiyah:
\begin{align} &\phantom{000}p+p+7+p+7-4 \\ &=p+p+p+7+7-4 \\ &=3p+10 \end{align}
Nkechi:
Fadekemi:Their total mark is , where is Safiyah's mark.
-
Abodunrin has \(₦\,n\) and Ikenna has \(₦\,20\) more. Abodunrin spends 500 kobo and Ikenna spends 750 kobo. Calculate how many kobos they have left altogether.
Abodunrin:
\begin{align} &\phantom{000}100n-500+100(n+20)-750 \\ &=100n-500+100n+2,000-750 \\ &=100n+100n-500+2,000-750 \\ &=200n+750 \end{align}
Ikenna:They have kobo left, where \(₦\,n\) is the original amount of money Abodunrin had.
-
A pencil costs \(₦\,x\). A ruler costs \(₦\,10\) less than a pencil. A pen costs \(₦\,5\) more than a ruler. The price of a small exercise book is twice the price of a ruler. Calculate the cost of 3 pencils, 2 rulers and 4 exercise books.
Pencil:
\begin{align} &\phantom{000}3x+2(x-10)+4(2x-20) \\ &=3x+2x-20+8x-80 \\ &=3x+2x+8x-20-80 \\ &=13x-100 \end{align}
Ruler:
Pen:
Exercise book:The cost is \(₦\,13x-100\), where \(₦\,x\) is the price of a pencil.
-
Rectangle 1 has a breadth of and a length of . Rectangle 2 has a breadth half as long as the breadth of Rectangle 1. The length of Rectangle 2 is longer than that of Rectangle 1. Calculate by how much the area of Rectangle 2 is larger than the area of Rectangle 1.
Breadth of Rectangle 1:
\begin{align} A_2-A_1&=x \times (y+10)-2x\times y \\ &= x(y+10)-2xy\\ &=xy+10x-2xy \\ &=10x-2xy+xy \\ &=10x-xy \end{align}
Length of Rectangle 1:
Breadth of Rectangle 2:
Length of Rectangle 2:The area of Rectangle 2 is larger than the area of Rectangle 1.
10.6 Summary
- An algebraic expression is a mathematical statement that contains a combination of numbers, symbols, variables and mathematical operators. It does not have an equals sign.
- A term can be a single number (positive or negative), or a variable, or one or more numbers and variables that are being multiplied together. Terms are separated by + or − signs.
- The coefficient is the number (factor) being multiplied by the variable. A coefficient can have a positive or negative value.
- A constant is a term without a variable. A constant can have a positive or negative value.
- To simplify an expression is to give it in its simplest form. We do this by collecting (combining) like terms using addition or subtraction.
- Like terms contain the same variable or variables.
- Unlike terms contain different variables.
- When we remove a bracket with a negative sign in front of it, we change the signs of all the terms inside the bracket.
- To expand an algebraic expression is to multiply what is outside the brackets (the coefficient of the bracket) by each of the terms that is inside the bracket.
- The distributive law states that the multiplying factor (the coefficient) can be distributed across each of the terms inside a bracket, so .
- When we simplify algebraic expressions, we must use the correct order of operations: Brackets, Of, Divide, Multiply, Add, Subtract.
