Chapter 13: Three-dimensional objects
A three-dimensional (3D) object has three dimensions that we can measure: we can measure the length, the breadth (or width) and the height of the object.
You will remember that a two-dimensional shape has only two dimensions that we can measure, which are length and breadth. So a two-dimensional shape is a shape on a flat surface.
But a three-dimensional object is like any object in the real world, such as a shoe, or a house, or a mobile phone. Three-dimensional objects are also called solid objects, because they stand up and have thickness.
The 3D objects that we will work with have specific properties.
-
Some 3D objects have flat faces, and others have curved faces.
-
The faces of some 3D objects are perpendicular to the base, and the faces of others tilt at an angle, to meet each other at a single point.
You will study the properties of different 3D objects in this chapter. Prisms (for example, cubes and cuboids), pyramids, cones, cylinders and spheres are all examples of 3D objects that have different properties.
13.1 Cubes and cuboids
One of the groups of 3D objects is called prisms. Examples of prisms are shown below.
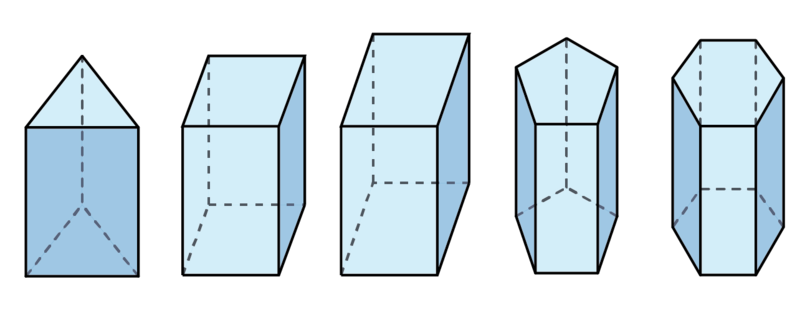
A prism has certain properties:
- A prism is a type of solid (3D object) that has a polygon as a base.
- The top face of a prism is exactly the same as the base of the prism.
- The top face of a prism is parallel to the base of the prism.
- The side faces of a prism are rectangles that are perpendicular to the base.
prism A prism is a solid figure with the top and bottom faces parallel to each other. The top and bottom faces are polygons and are exactly the same. The side faces of a prism are rectangles.
polygon A polygon is a closed flat shape with three or more straight sides.
We are going to study the properties of two types of prisms, namely cubes and cuboids.
Cubes
A cube is a 3D object that is formed by six equal squares.
There are many real-life objects in the shape of a cube, and some examples are shown below.
A dice is a cube.

Children often play with blocks in the form of cubes.
Perhaps you have seen a box in the shape of a cube.

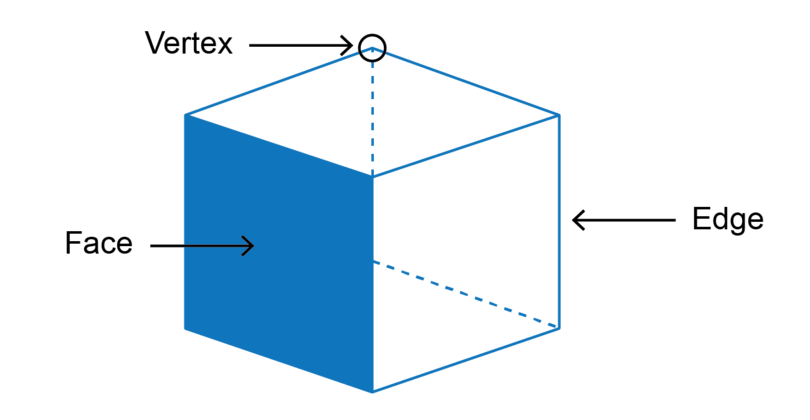
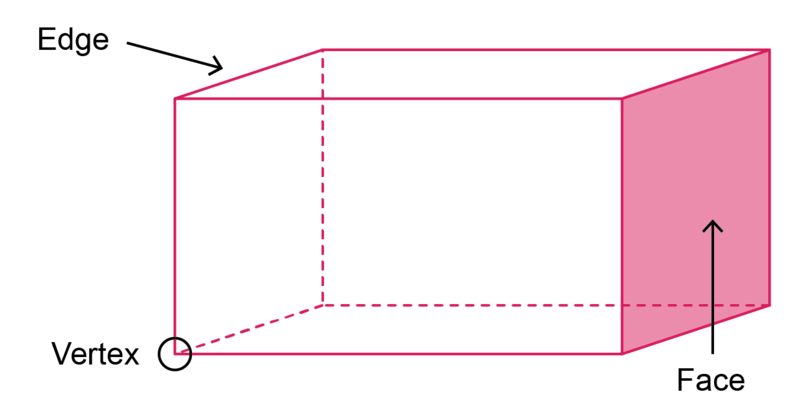
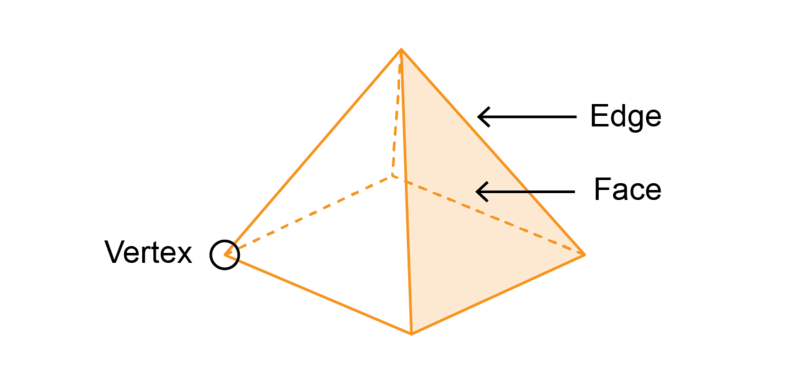
There are certain words that we need to use when we describe the properties of 3D objects, such as face, base, edge and vertex. You will learn the meaning of these words as you work through this chapter.
The properties of a cube are:
-
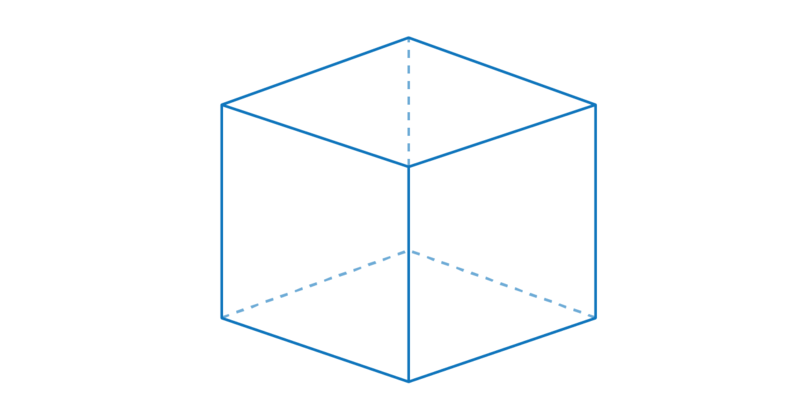
The flat parts of a cube are called faces. A cube has six faces, and each face is a square. All the squares have the same size.
In the diagram below, the base is shaded. The base is a square. The base is one of the faces.
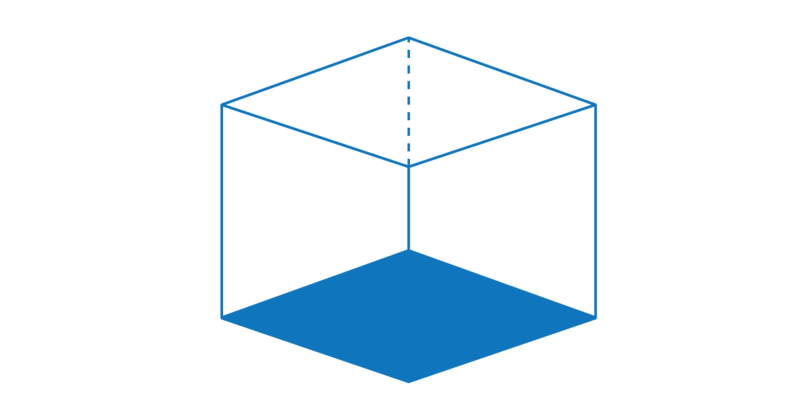
In the diagram below, the top face is shaded. The top face is a square. The base and the top are parallel to each other.
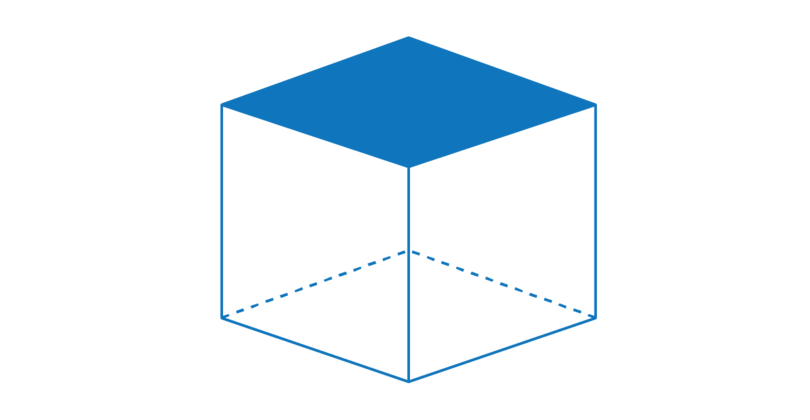
In the diagram below, one of the side faces is shaded. There are four side faces. Each side face is a square.
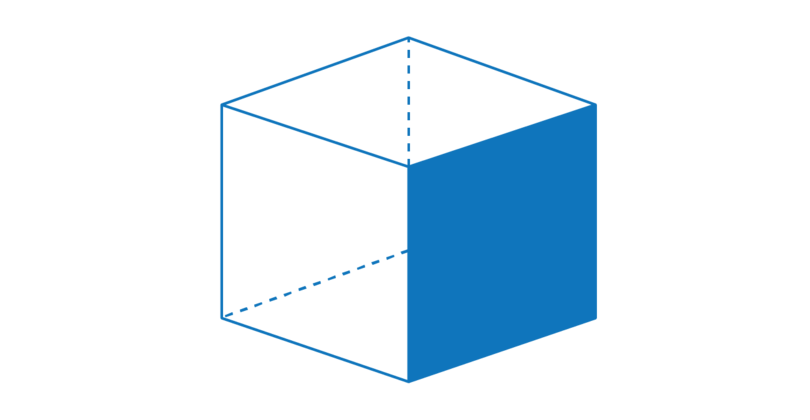
-
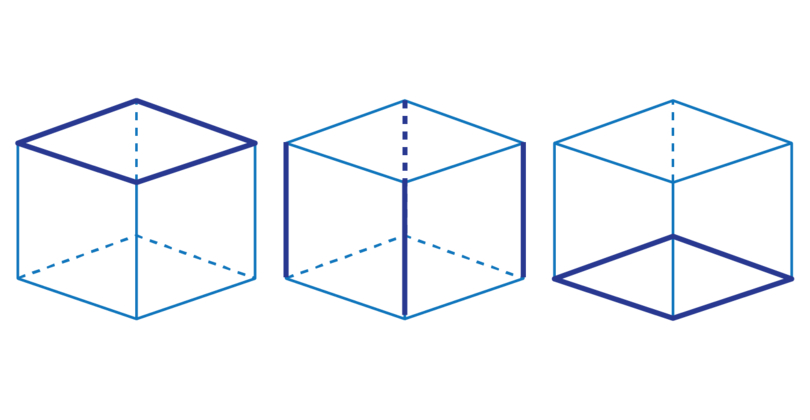
The faces of a cube meet each other at an edge. A cube has twelve edges: four edges around the top face of the cube, four edges around the side faces, and four edges around the base of the cube.
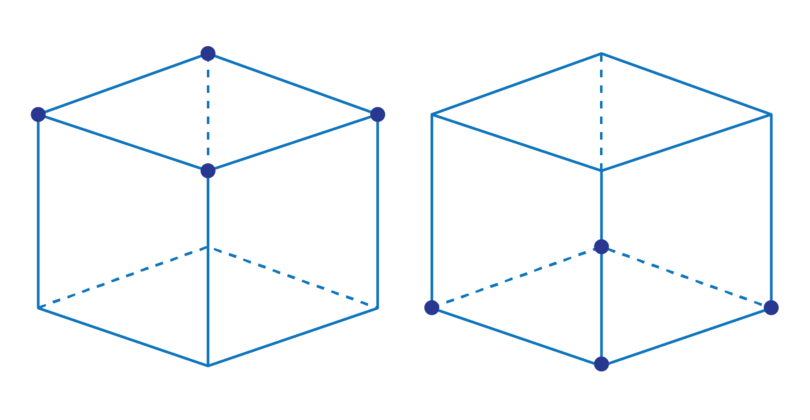
- The edges of a cube meet each other at a vertex. A cube has eight vertices: four at the top of the cube and four at the base of the cube.
cube A cube is a 3D object that is formed by six equal squares.
face A face is a flat surface of a 3D shape.
base The base is the flat surface at the bottom of a 3D object on which the object stands.
edge The edge is the line where two faces meet.
vertex The vertex is a point where three edges meet. The plural of vertex is vertices.
A cube is a prism, because the base and top face are squares, and a square is a polygon. The side faces of a cube are also squares, which are a special type of rectangle. The side faces are perpendicular to the base of the cube.
Worked example 13.1: Identifying the parts of a cube
Consider the cube given below.
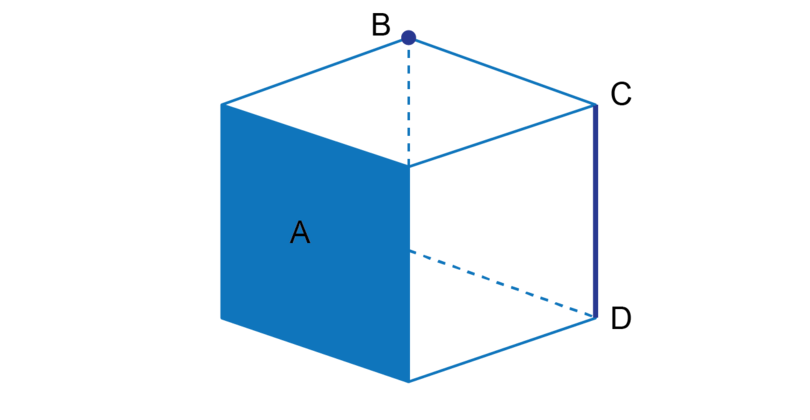
What is the shaded area labelled called?
-
Step 1: Recall the properties of a cube.
A cube is formed by six squares, called faces.
The faces of a cube meet each other at an edge.
The edges of a cube meet each other at a vertex. -
Step 2: Identify the shaded part and give the correct answer.
The shaded area labelled is a face of the cube.
What is the point labelled (in the first diagram) called?
-
Step 1: Recall the properties of a cube.

A cube is formed by six squares, called faces.
The faces of a cube meet each other at an edge.
The edges of a cube meet each other at a vertex. -
Step 2: Identify the point labelled and give the correct answer.
The point labelled is a vertex of the cube.
What is the line labelled called?
-
Step 1: Recall the properties of a cube.
A cube is formed by six squares, called faces.
The faces of a cube meet each other at an edge.
The edges of a cube meet each other at a vertex. -
Step 2: Identify the line labelled and give the correct answer.
Line is an edge of the cube.
Worked example 13.2: Describing the properties of a cube
Consider the 3D object given below.

How many faces does a cube have?
-
Step 1: Recall what the face of a cube is.

The flat parts of a cube are called faces. A cube has six faces and each face is a square.
-
Step 2: Visualise a cube and give the correct answer.
A cube has 6 faces.
What is the shape of the faces of a cube?
-
Step 1: Recall the properties of a cube.

A cube has 6 faces and each face is a square. All the squares have the same size.
-
Step 2. Give the correct answer.
All the faces of a cube are squares.
How many edges does a cube have?
-
Step 1: Recall what the edge of a cube is.
The faces of a cube meet each other at an edge.

-
Step 2: Visualise a cube and give the correct answer.
A cube has 12 edges.
How many vertices does a cube have?
-
Step 1: Recall what the vertices of a cube are.
The edges of a cube meet each other at a vertex.

-
Step 2: Visualise a cube and give the correct answer.
A cube has 8 vertices.
Exercise 13.1: Identify the parts of a cube
Consider the diagram of the 3D object below.

-
What is the name of the 3D object?
The 3D object is a cube.
-
What is the name of the shaded area labelled ?
The shaded area labelled is a face of the cube.
-
What shape is the shaded area labelled ?
Each face of a cube is a square, so the shaded area labelled is a face of a cube.
-
What is the name of the line labelled ?
The line is an edge of the cube. The faces of a cube meet each other at an edge.
-
What is the name of the point labelled ?
The point is a vertex of the cube. The edges of a cube meet each other at a vertex.
Exercise 13.2: Describe the properties of a cube
-
Select a word from Column B that best fits the description in Column A. Write down only the number for the description in Column A, and the capital letter that gives the correct answer from Column B.
Column A Column B a) The six squares that form the flat parts of a cube. A edges b) The lines where two faces of a cube meet each other. B vertices c) The points where the edges of a cube meet each other. C faces a) C
b) A
c) B
-
Complete the table given below.
Properties of a cube
Number and shape of faces Number of edges Number of vertices Properties of a cube
Number and shape of faces Number of edges Number of vertices 6 squares 12 edges 8 vertices
Cuboids
A cuboid is formed by three pairs of rectangles. Each pair of rectangles is opposite each other and equal in size.
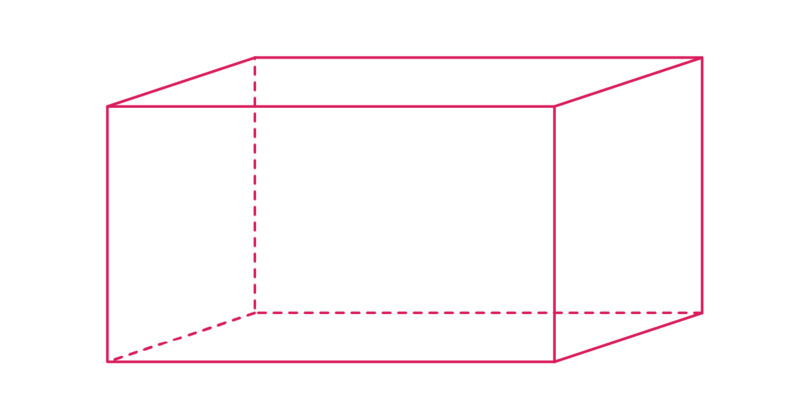
There are many real life objects in the shape of a cuboid, such as those shown in the examples below.
A brick is a cuboid.

When you buy new shoes in a box, the shoe box is in the shape of a cuboid.

Many different foods, for example, breakfast cereals, are sold in boxes in the shape of cuboids.

The properties of a cuboid are:
-
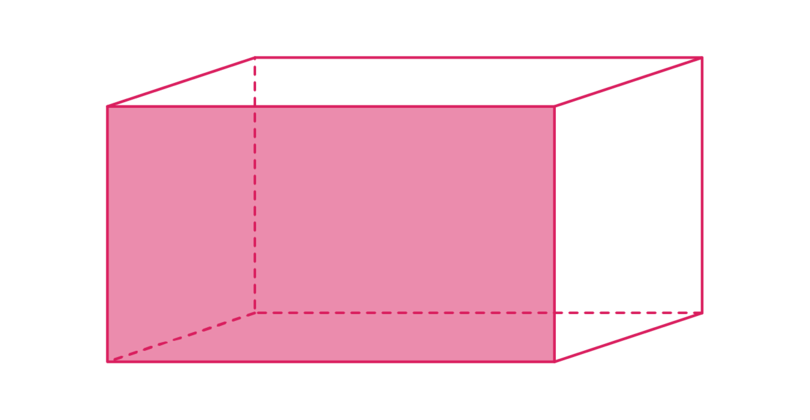
A cuboid has six faces and each face is a rectangle. The two faces that are opposite each other are equal. So a cuboid has three pairs of equal rectangles.
In the diagram below, the base and the top face are shaded. The base is a rectangle and is equal to the top face.

In the diagram below, the "left" face and the "right" faces are shaded. Both these faces are rectangles and they are equal to each other.
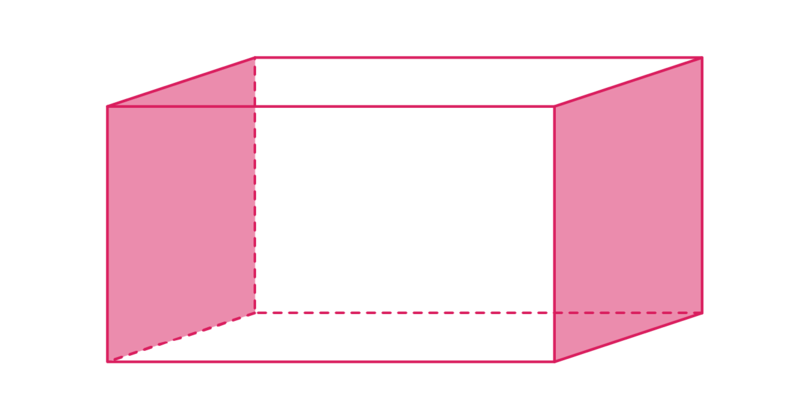
In the diagram below, the "front" face is shaded. The "front" face is a rectangle. The "front" rectangle is equal to the "back" rectangle.
-
Two faces of a cuboid meet each other at an edge. A cuboid has twelve edges: four edges around the top face of the cuboid, four edges around the side faces, and four edges around the base of the cuboid.
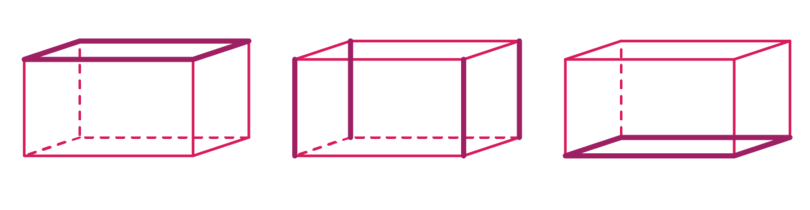
-
The edges of a cuboid meet each other at a vertex. A cuboid has eight vertices: four at the top of the cuboid and four at the base of the cuboid.
Remember that vertices is the plural of vertex. So we refer to one vertex and eight vertices.
cuboid A cuboid is a prism formed by three pairs of rectangles. The rectangles opposite each other are equal to each other.
A cuboid is a prism, because it has a rectangle as a base and a rectangle is a polygon. The side faces of a cuboid are rectangles that are perpendicular to the base of the cuboid.
Worked example 13.3: Identifying the parts of a cuboid
Consider the cuboid given below.
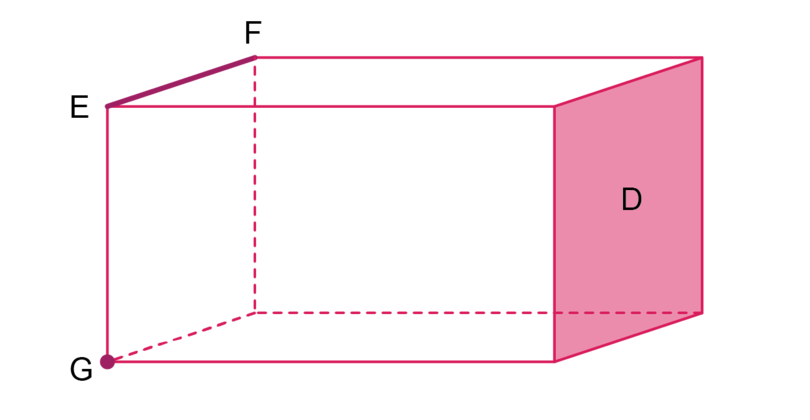
What is the shaded area labelled called?
-
Step 1: Recall the properties of a cuboid.
A cuboid is formed by three pairs of equal rectangles, called faces. Opposite faces are equal.
The faces of a cuboid meet each other at an edge.
The edges of a cuboid meet each other at a vertex. -
Step 2: Identify the shaded part and give the correct answer.
The shaded area labelled is a face of the cuboid.
What is the line labelled called?
-
Step 1: Recall the properties of a cuboid.
A cuboid is formed by three pairs of equal rectangles, called faces. Opposite faces are equal.
The faces of a cuboid meet each other at an edge.
The edges of a cuboid meet each other at a vertex. -
Step 2: Identify the line labelled and give the correct answer.
Line is an edge of the cuboid.
What is the point labelled called?
-
Step 1: Recall the properties of a cuboid.
A cuboid is formed by three pairs of equal rectangles, called faces. Opposite faces are equal.
The faces of a cuboid meet each other at an edge.
The edges of a cuboid meet each other at a vertex. -
Step 2: Identify the point labelled and give the correct answer.
Point is a vertex of the cuboid.
Worked example 13.4: Describing the properties of a cuboid
Consider the 3D object given below.

How many faces does a cuboid have?
-
Step 1: Recall what the face of a cuboid is.

The flat parts of a cuboid are called faces.
A cuboid is formed by three pairs of equal rectangles. The opposite faces of a cuboid are equal. -
Step 2: Visualise a cuboid and give the correct answer.
A cuboid has 6 faces.
What are the shapes of the faces of a cuboid?
-
Step 1: Recall the properties of a cuboid.

A cuboid is formed by three pairs of equal rectangles.
-
Step 2. Give the correct answer.
All the faces of a cuboid are rectangles.
How many edges does a cuboid have?
-
Step 1: Recall what the edge of a cuboid is.

The faces of a cuboid meet each other at an edge.
-
Step 2: Visualise a cuboid and give the correct answer.
A cuboid has 12 edges.
How many vertices does a cuboid have?
-
Step 1: Recall what the vertices of a cuboid are.

The edges of a cuboid meet each other at a vertex.
-
Step 2: Visualise a cuboid and give the correct answer.
A cuboid has 8 vertices.
Exercise 13.3: Describe the parts of a cuboid
Consider the diagram of 3D object below.

-
What is the name of the 3D object?
The 3D object is a cuboid.
-
What part of the 3D object is shaded and labelled ?
The shaded area is a face of the cuboid.
-
What shape is the shaded area labelled ?
Each face of a cuboid is a rectangle, so the shaded area is a rectangle.
-
Name and describe the line labelled .
The line is an edge of the cuboid. The faces of a cuboid meet each other at an edge.
-
Name and describe the point labelled ?
The point is a vertex of the cuboid. The edges of a cuboid meet each other at a vertex.
Exercise 13.4: Describe the properties of a cuboid
-
Select a word from Column B that best fits the description in Column A. Write down only the number for the description in Column A, and the capital letter that gives the correct answer from Column B.
Column A Column B a) The three pairs of equal rectangles that form the flat parts of a cuboid. A vertices b) The lines where the faces of a cuboid meet each other. B faces c) The points where the edges of a cuboid meet each other. C edges a) B
b) C
c) A
-
Complete the table given below.
Properties of a cuboid
Number and shape of faces Number of edges Number of vertices Properties of a cuboid
Number and shape of faces Number of edges Number of vertices 6 rectangles 12 edges 8 vertices
13.2 Pyramids
A pyramid is an object that has a polygon as its base and sides that converge (meet each other) at one single point. The sides are not perpendicular to the base.
There are many real life objects in the form of a pyramid. The pyramids of Egypt are well known.

A pile of eggs can be stacked in a pyramid.

The roof of a house can be in the shape of a pyramid.

A pyramid can have any polygon (for example, a rectangle or a pentagon or a hexagon) as its base.
We will focus on a pyramid that has a square as its base.
The properties of a pyramid are:
-
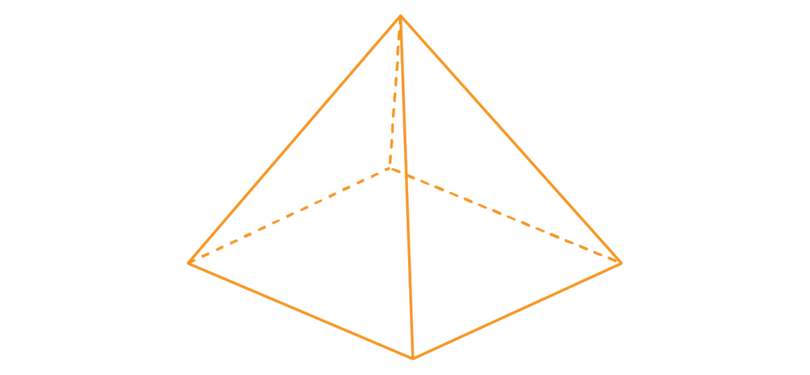
A square-based pyramid has five faces.
A square-based pyramid has a square as a base.
In the diagram below, the base is shaded. The base of this pyramid is a square.
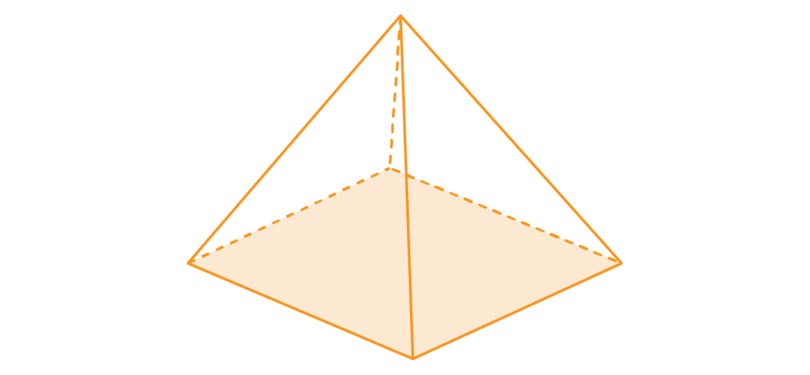
The side faces are four triangles. The triangles are isosceles triangles and they are all equal.
In the diagram below, one of the side faces is shaded.
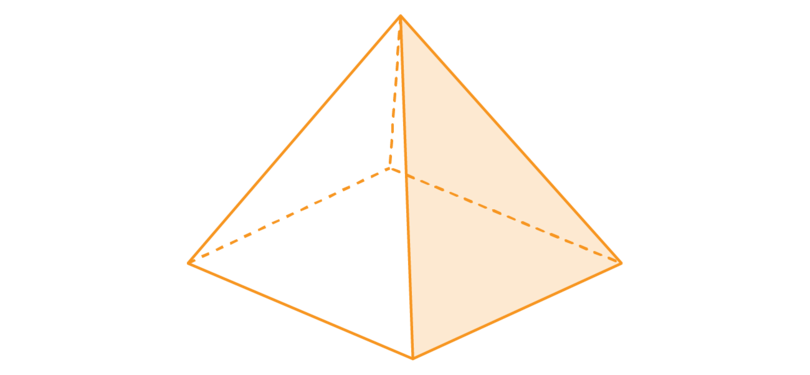
-
The faces of a pyramid meet each other at an edge.
A square-based pyramid has eight edges: four edges around the base of the pyramid, and four edges formed by the triangles that are the side faces of the pyramid.
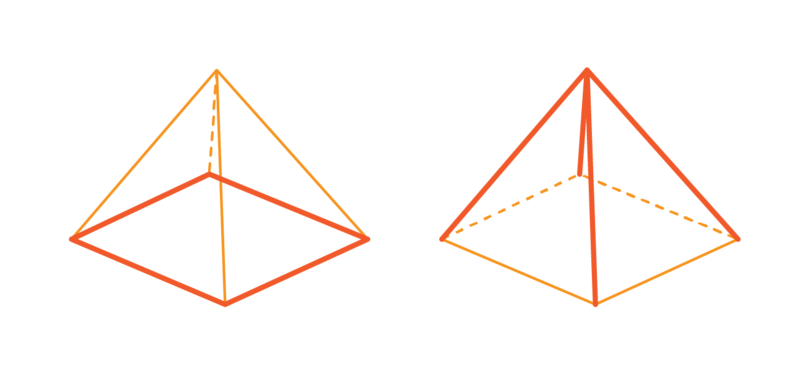
-
The edges of a pyramid meet each other at a vertex.
A square based pyramid has five vertices: four at the base of the pyramid and one at the top of the pyramid where the triangles meet each other.
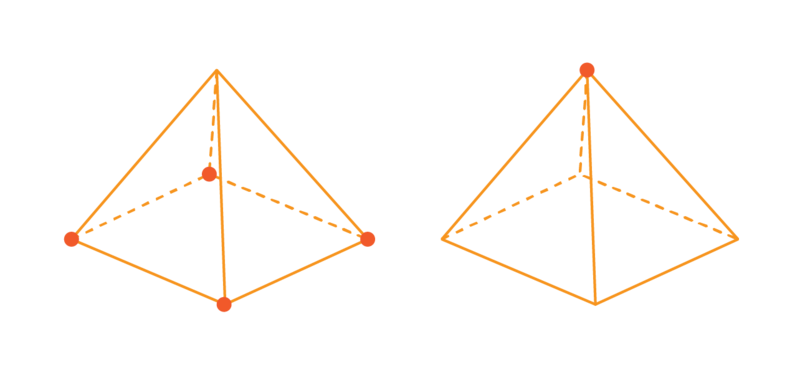
The top vertex has a special name. The edges of the triangles that form the side faces converge at a vertex called the apex.
We call a pyramid a "right pyramid" if the line between the apex and the centre of the base is perpendicular to the base.
pyramid A pyramid is a 3D object that has a polygon as its base. The side faces are triangles that meet each other at one single point, the apex.
converge To converge is to move towards each other and to meet at one point.
apex The apex is the top-most point that is furthest from the base of a 3D object.
A pyramid is NOT a prism, because the side faces are not rectangles and the side faces are not perpendicular to the base.
Worked example 13.5: Describing the parts of a pyramid
Consider the square-based pyramid given below.
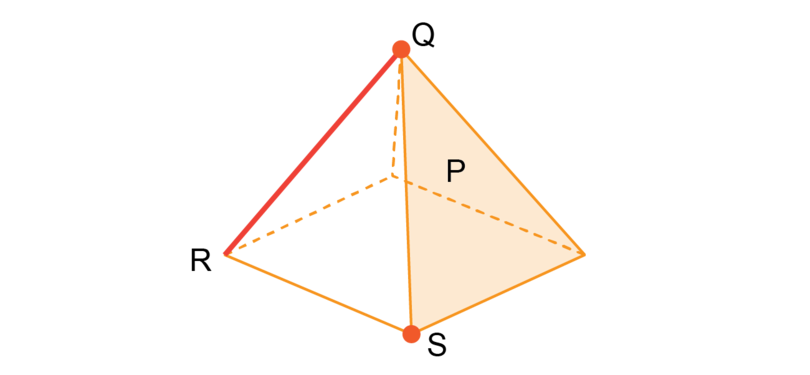
What is the name of the shaded area labelled ?
-
Step 1: Recall the properties of a pyramid.
-
Step 2: Identify the shaded area and give the correct answer.
The shaded area is a face of the pyramid.
What is the shape of the base of this pyramid?
-
Step 1: Identify the shape of the base of the pyramid and give the correct answer.
The base of the pyramid is a square.
What is the shape of the side faces of the pyramid?
-
Step 2: Identify the shape of the side faces and give the correct answer.
The side faces are triangles.
What is the name of the line labelled ?
-
Step 1: Recall the properties of a pyramid.

-
Step 2: Identify the line labelled and give the correct answer.
The line labelled is an edge of the pyramid.
What is the name of the point labelled ?
-
Step 1: Recall the properties of a pyramid.

-
Step 2: Identify the point labelled and give the correct answer.
The point labelled is a vertex of the pyramid.
What is the special name of the point labelled ?
-
Step 1: Recall the properties of a pyramid.
The top vertex has a special name. The edges of the triangles that form the side faces converge at a vertex called the apex.
-
Step 2: Identify the point labelled and give the correct answer.
The point labelled is the apex of the pyramid.
Exercise 13.5: Identify the parts of a pyramid
Consider the 3D object given below.

-
What is the name of the 3D object?
The 3D object is a pyramid. The base of this pyramid is a square, so it is a square-based pyramid.
-
How many faces does the object have?
The object (a pyramid) has one base and four side faces, so the pyramid has five faces.
-
What are the shapes of the faces?
The base is a square and the side faces are triangles.
-
How many edges does the pyramid have?
The pyramid has 8 edges.
-
How many vertices does the pyramid have?
The pyramid has 5 vertices.
-
What is the name of the one point where all the triangles meet each other?
The special vertex at the top is called the apex.
Exercise 13.6: Describe the properties of a pyramid
-
Select a word from Column B that best fits the description in Column A.
Column A Column B a) The base and triangles that form the flat parts of a pyramid. A vertices b) The lines where the faces of a pyramid meet each other. B apex c) The points where the edges of a pyramid meet each other. C edges d) The special point where all the side faces meet each other. D faces a) D
b) C
c) A
d) B
-
Complete the table given below.
Properties of a square-based pyramid
Number and shape of faces Number of edges Number of vertices Properties of a square-based pyramid
Number and shape of faces Number of edges Number of vertices 1 square and 4 triangles 8 edges 5 vertices
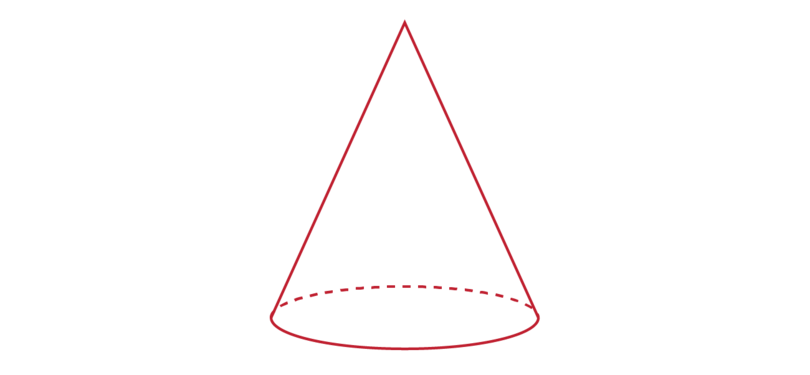
13.3 Cones
A cone is another example of a 3D object that has an apex.
There are many examples of cones in real life.
We can buy ice cream in a cone. The part of the ice cream that you hold in your hand is the cone.

The round ball of ice cream that you eat is a sphere. You will study the properties of a sphere later in this chapter.
We can make a party hat in the form of a cone.

The roof of a house can be in the form of a cone.

The circular walls of the round houses are cylinders. You will study the properties of a cylinder later in this chapter.
The properties of a cone are:
-
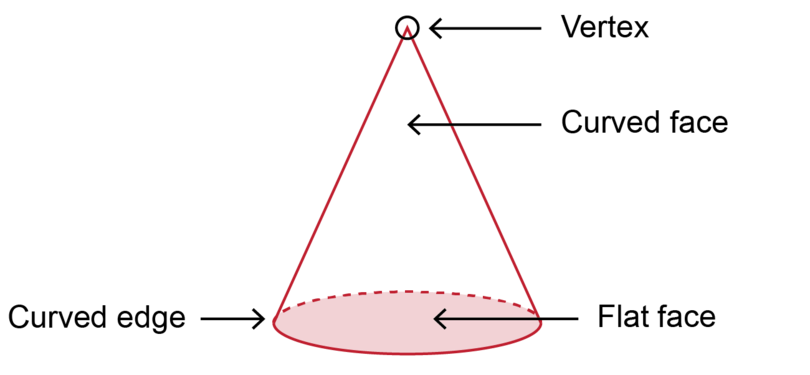
A cone has two faces. One of the faces is flat and the other face is curved.
The base of a cone is a flat circle.

A cone has only one side face, and this face is curved.
Draw a circle and cut it out. Then cut out a "slice" (a sector) of the circle as shown below.
Curl the paper around so that fits onto . You are now holding the curved face of a cone in your hand. Although this face is curved, it can be laid flat, so it is still a face.
-
A cone has only one edge. The edge of a cone is not a straight line - it is a curve.
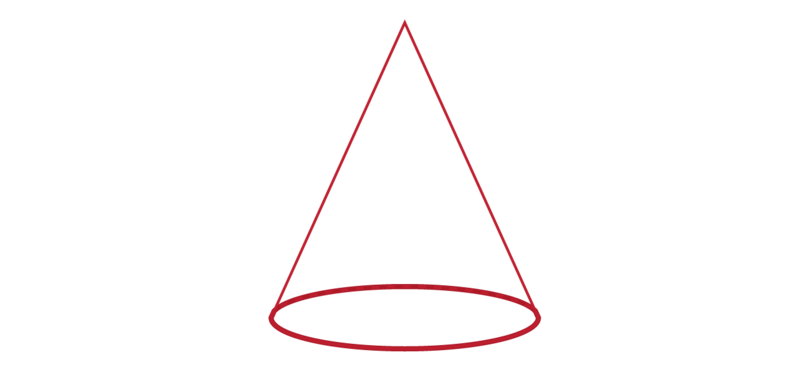
The edge of a cone is the circumference of the circle that forms the base of the cone.
-
A cone has only one vertex.
The vertex of a cone is at the top of the cone.
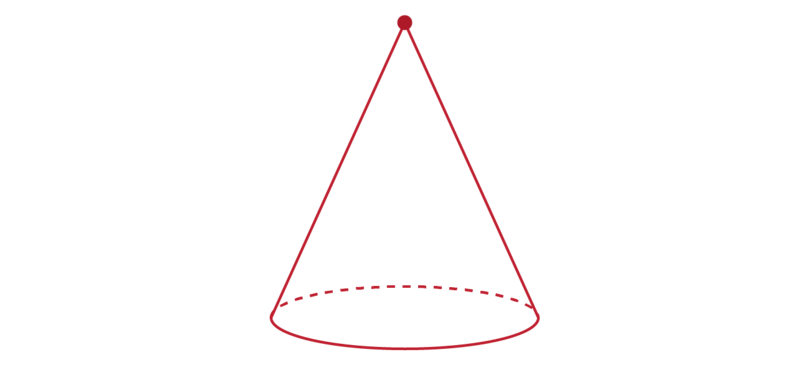
The one vertex of a cone is also called the apex of the cone.
From the base, the curved face becomes narrower until it forms a point at the top, which is the apex.
cone A cone is a 3D object with a circle as its base. A cone has one curved side face that comes to a point, the apex.
A cone is NOT a prism: a cone has a circle as its base, and a circle is not a polygon. A prism has a polygon as a base.
Worked example 13.6: Identifying the parts of a cone
Consider the diagram of the cone given below.
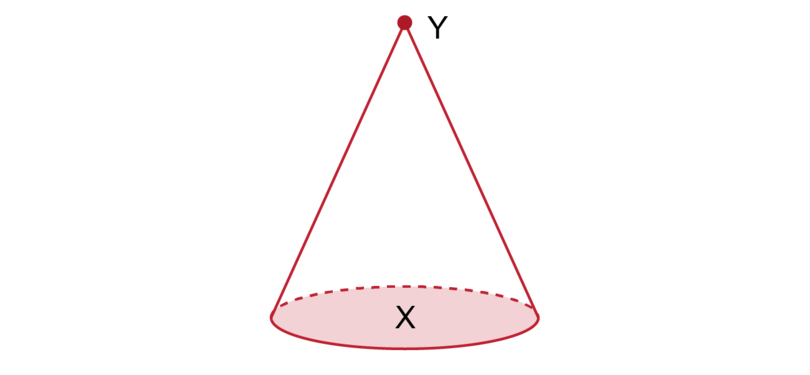
What is the name of the shaded area labelled ?
-
Step 1: Recall the properties of a cone.
A cone has a circle as its base. It has only one curved side face that narrows until it forms a point at the top, which is the apex.
-
Step 2: Identify the shaded area and give the correct answer.
The shaded area labelled is the base of the cone.
What shape is shaded area labelled ?
-
Step 1: Recall the properties of a cone.
A cone has a circle as its base.
-
Step 2: Identify the shape and give the correct answer.
The base of the cone is a circle.
Is the edge of a cone a straight line or a curve?
-
Step 1: Recall the properties of a cone.
A cone has a circle as its base. It has only one curved side face that tapers to a single point at the apex.
-
Step 2: Identify the edge of the cone and give the correct answer.
The edge of a cone is curved. The edge of a cone is the circumference of the circle that is the base of the cone.
What is the name of the point labelled ?
-
Step 1: Recall the properties of a cone.
A cone has a circle as its base. It has only one curved side face that tapers to a single point at the apex.
-
Step 2: Identify the point labelled and give the correct answer.
The point is the vertex of the cone. It is also called the apex of the cone.
Exercise 13.7: Describe the parts of a cone
Consider the diagram of a 3D object given below.

-
What is the name of the 3D object?
The 3D object is a cone.
-
What letter on the diagram shows the base of the object?
The letter shows the base of the cone.
-
What shape is the base of the object?
The base of the cone is a circle.
-
What is the name of the point labelled ?
The point is the vertex of the cone. It is also called the apex of the cone.
-
Why is the edge of a cone not a straight line but a curve?
The edge of a cone is a curve, because the edge of a cone is the circumference of the circle that is the base of the cone.
Exercise 13.8: Describe the properties of a cone
-
Select a word from Column B that best fits the description in Column A.
Column A Column B a) The flat circle that forms part of a cone. A vertex or apex b) The circumference of the circle which is the base of the cone. B base c) The point at the top of a cone. C edge a) B
b) C
c) A
-
Complete the following table.
Properties of a cone
Number and shape of faces Number of edges Number of vertices Properties of a cone
Number and shape of faces Number of edges Number of vertices 1 flat circle as base and 1 curved side face 1 curved edge 1 vertex (the apex)
13.4 Cylinders
In a cylinder, both the top and bottom faces are circles. The top and bottom faces are joined by a curved surface that is perpendicular to the base.
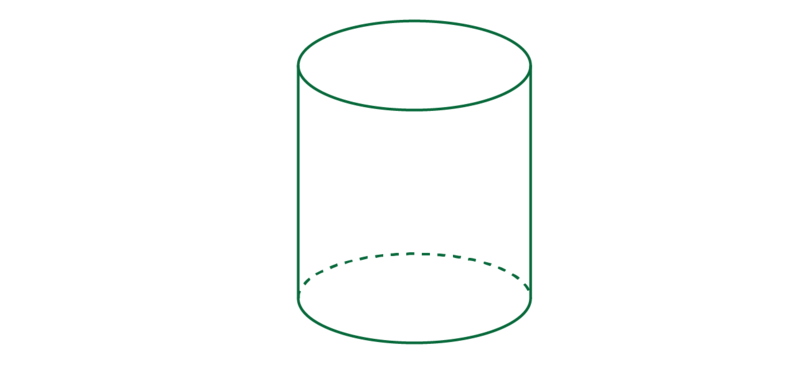
There are many real life objects in the form of a cylinder.
Paint is sold in tins that are cylinders.

Batteries for a radio are in the form of cylinders.

Any plastic water pipe is an example of a cylinder. In this case the cylinder is open, because it has no base or top face.

The properties of a cylinder are:
-
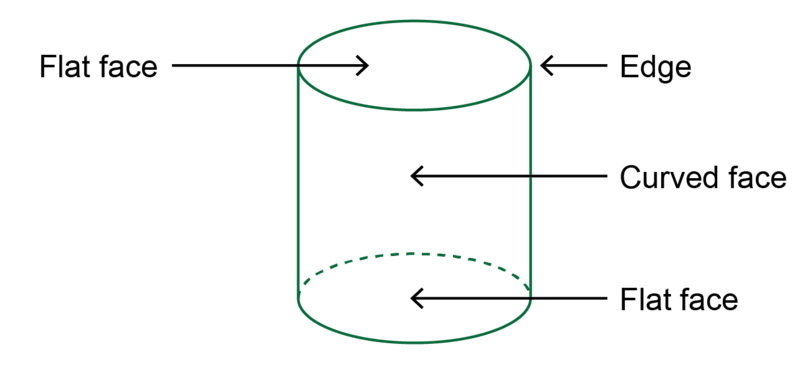
A cylinder has two flat faces and one curved face:
In the diagram below, the base, which is the bottom face, of the cylinder is shaded. The base of a cylinder is a circle.

The top face of a cylinder is also a circle. The two circles are equal. In the diagram below, the base and the top face are shaded.

The two circles are joined by a curved surface. The inner part of a toilet roll is the curved surface of a cylinder. If you cut it open as shown below, it will unfold into a rectangle.

So, a cylinder has three faces: two flat circles and one curved surface.
-
The faces of a cylinder meet each other at two edges.
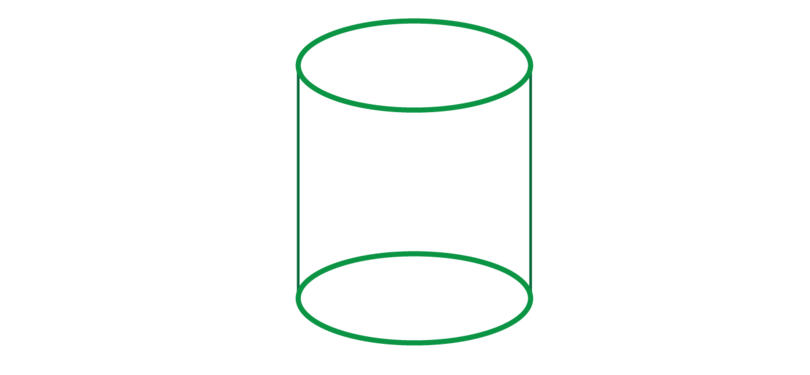
The edges are not straight lines. They are curves, because they are the circumferences of the two circles that form the base and the top of the cylinder.
cylinder A cylinder is a 3D object with two equal circles as the base and the top face. A cylinder has one curved side face that is perpendicular to the two circles.
A cylinder does not have a vertex.
A cylinder is NOT a prism: a prism has a circle as its base and a circle is not a polygon.
Worked example 13.7: Identifying the parts of a cylinder
Consider the diagram of a cylinder given below.
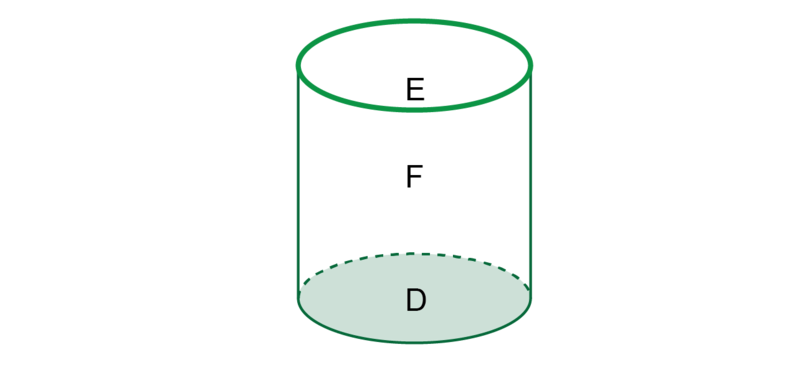
What part of the cylinder is shaded and labelled ?
-
Step 1: Recall the properties of a cylinder.
-
Step 2: Identify the shaded area labelled and give the correct answer.
The shaded area is the base of the cylinder. The base is one of the faces of the cylinder.
What part of the cylinder is shown by the circle labelled ?
-
Step 1: Recall the properties of a cylinder.
-
Step 2: Identify the circle labelled and give the correct answer.
is an edge of the cylinder.
What part of the cylinder is labelled ?
-
Step 1: Recall the properties of a cylinder.
-
Step 2: Identify the part labelled and give the correct answer.
The area labelled is the curved surface that forms one of the faces of the cylinder.
Exercise 13.9: Identify the parts of a cylinder
Consider the 3D object shown below.

-
What is the name of the 3D object?
The 3D object is a cylinder.
-
What is the shaded area labelled called?
The shaded area is the base of the cylinder. The base is one of the faces of the cylinder.
-
What is the shape of the area labelled ?
The area labelled is a circle.
-
What letter on the diagram shows an edge of the cylinder?
The letter shows an edge of the cylinder.
-
Why does the letter show a curve and not a straight line?
An edge of a cylinder is not a straight line. shows a curve, because it shows the circumference of the circle that forms the top of the cylinder.
-
What part of the cylinder is labelled ?
The area labelled is the curved surface of the cylinder. The curved surface is one of the faces of the cylinder.
Exercise 13.10: Describe the properties of a cylinder
-
Select a word from Column B that best fits the description in Column A:
Column A Column B a) The flat circle at the bottom of a cylinder. A vertex b) The circumferences of the circles at the top and the bottom of a cylinder. B edges c) A cylinder does not have one of these. C base a) C
b) B
c) A
-
Complete the following table.
Properties of a cylinder
Number and shape of faces Number of edges Number of vertices Properties of a cylinder
Number and shape of faces Number of edges Number of vertices 2 flat circles (base and top) and 1 curved side face 2 curved edges No vertex
13.5 Spheres
Spheres are solids that are perfectly round and look the same from any direction.
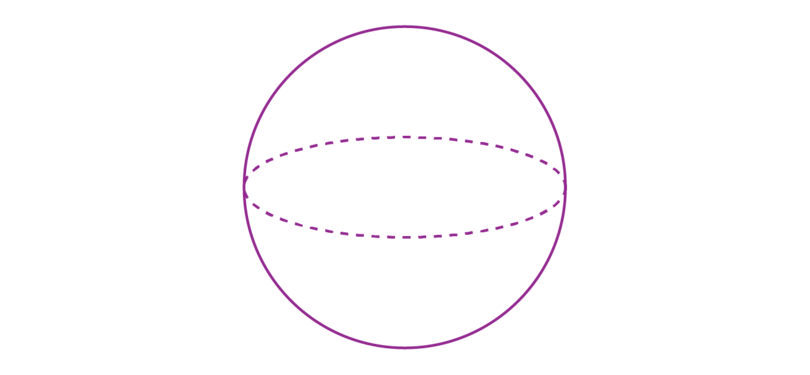
There are many real life objects in the shape of a sphere.
A football is a sphere.

Many children all over the world play with glass marbles.

The earth is almost a perfect sphere. (The earth is a bit flatter at the two poles.)

There is only one basic property of a sphere:
- A sphere has only one curved face. If you were asked to paint a ball, you would paint the curved face of the ball.
sphere A sphere is a 3D object consisting of one curved face.
A sphere has no edges, and no vertices.
A sphere has no flat faces. This means that a sphere is not a prism, as a prism has only flat faces.
Worked example 13.8: Identifying the parts of a sphere
Consider the diagram of a sphere given below.

How many faces does a sphere have?
-
Step 1: Recall the properties of a sphere.
-
Step 2: Identify the face of a sphere and give the correct answer.
A sphere has only one face.
Is the face of the sphere flat or curved?
-
Step 1: Recall the properties of a sphere.
-
Step 2: Consider what the face of a sphere is like, and give the correct answer.
A sphere has a curved face.
State whether the following statement is true or false:
A sphere has one edge and no vertices.
-
Step 1: Recall the properties of a sphere.
-
Step 2: Read the question carefully and give the correct answer.
The statement is false. A sphere has no edges and no vertices.
Exercise 13.11: Identify the parts of a sphere
Consider the 3D object shown below.

-
Identify the type of 3D object.
The 3D object is a sphere.
-
Describe the properties of the object.
The sphere has one curved face. The sphere has no edges, and no vertices.
Exercise 13.12: Describe the properties of 3D objects
-
Identify each of the 3D objects shown below.

A: cube
B: cuboid
C: pyramid
D: cone
E: cylinder
F: sphere
-
Consider the following 3D objects: cube, cuboid, pyramid, cone, cylinder and sphere. Write the name of each of the 3D objects in the correct column of the table below.
Only flat faces Only curved faces Flat and curved faces Only flat faces Only curved faces Flat and curved faces cube; cuboid; pyramid sphere cone; cylinder -
Select a word from Column B that best fits the description in Column A.
Column A Column B a) A 3D object with no edges and no vertices. A pyramid b) A 3D object formed by one square and four triangles. B cone c) A 3D object with three pairs of equal rectangles. C cube d) A 3D object formed by six squares. D sphere e) A 3D object formed by one circle and one curved surface. E cylinder f) A 3D object formed by two circles and one curved surface. F cuboid a) D
b) A
c) F
d) C
e) B
f) E
-
Complete the table below.
Name of 3D object Number of faces Number of edges Number or vertices cube cuboid pyramid (square as base) cone cylinder sphere Name of 3D object Number of faces Number of edges Number or vertices cube 6 12 8 cuboid 6 12 8 pyramid (square as base) 5 8 5 cone 2 1 1 cylinder 3 2 0 sphere 1 0 0
13.6 Volume of cubes and cuboids
Volume is the amount of the space that a 3D object takes up. Volume is a way of measuring the size of a whole 3D object. It is measured in cubic units.
-
When we measure length, we measure one dimension. The length of the line below is . We say the length of the line is "1 centimetre".

-
When we measure area, we measure two dimensions. The square below has a length of 1 cm and a breadth (or width) of 1 cm. The area of the square is . We say the area is "1 square centimetre".

-
When we measure volume. we measure three dimensions. The cube below has a length of 1 cm, a breadth of 1 cm and a height of 1 cm. The volume of the cube is . We say the volume is "1 cubic centimetre".
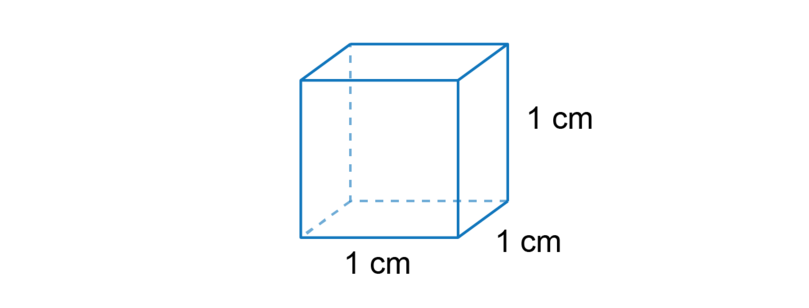
When we calculate the volume of a container, we work out how many cubes we can pack into the container.
We start by finding out how many cubes will cover the base of the container.
In the container below, it is possible to pack 6 cubes across the length of the container and 4 cubes across the breadth of the container.

To find the number of cubes for one layer, we multiply the number of cubes along the length by the number of cubes along the breadth.
\begin{align} \text {Number of cubes for one layer} &= 6 \times 4\\ &= 24 \end {align}To fill the whole container, we pack more layers. In the container below it is possible to pack 8 layers.
This container is a prism, so each layer will have the same number of cubes. To find the total number of cubes we multiply the number of cubes in one layer by the number of layers.
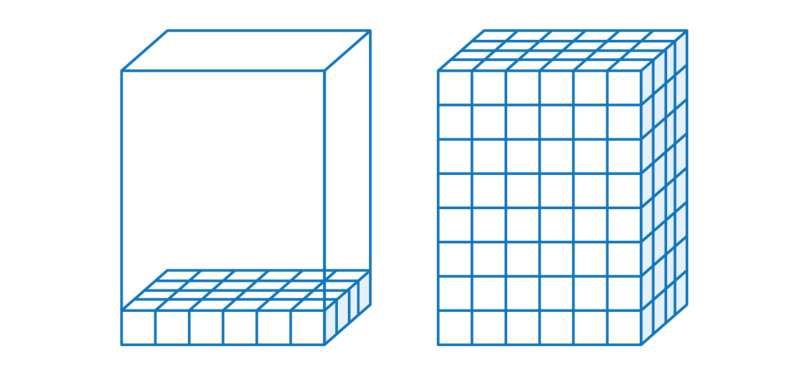
From this calculation, we can see that we calculate the volume of a prism by multiplying the area of the base of the prism by the height of the prism.
The volume of a prism is calculated using this formula:
This formula can be used to calculate the volume of any prism. The prism can have a triangle or a pentagon or a hexagon as its base, and this formula will still hold.
Worked example 13.9: Calculating the volume of a cube
Find the volume of the following cube.
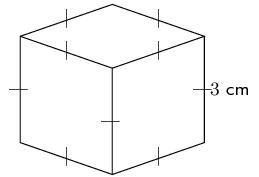
-
Step 1: A cube is a prism. Write down the formula to find the volume of a prism.
-
Step 2: Find the area of the base of the cube. The base of a cube is a square.
\begin{align} \text{Area of square} & = {s}^{2} \\ & = {3}^{2} \\ & = \text{9 cm}^{2} \end{align} -
Step 3: Multiply the area of the base by the height of the prism to find the volume.
\begin{align} \text{Volume} & = \text{area of base}\times \text{height of prism} \\ & = 9\times 3 \\ & = \text{27}\text{ cm}^{3} \end{align} -
Step 4: Write the final answer, and remember to give the correct units.
The volume of the cube is .
Worked example 13.10: Calculating the volume of a cuboid
The 3D object shown below is a cuboid. The height of the cuboid is 12 cm, the length is 13 cm, and the breadth is 6 cm. Calculate the volume of the object.
The diagram is not necessarily drawn to scale.
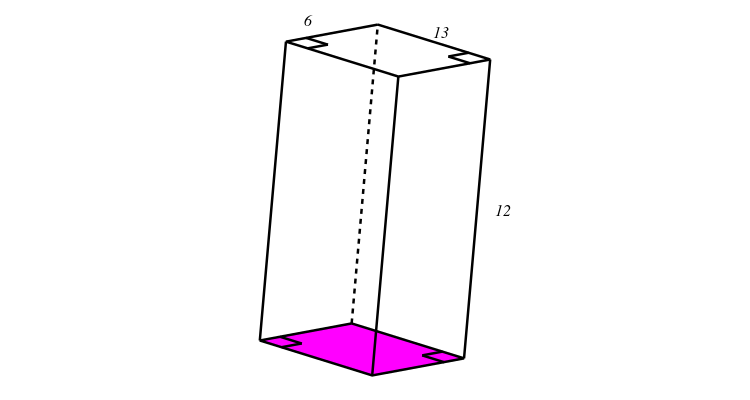
-
Step 1: A cuboid is a prism. Write down the formula to find the volume of a prism.
-
Step 2: Find the area of the base of the cuboid.
The purple rectangle at the bottom of the prism is the base of the cuboid. The purple rectangle at the bottom is the same size as the rectangle on the top.
\begin{align} \text{Area of rectangle} & = l \times b \\ & = 13 \times 6 \\ & = \text{78 cm}^{2} \end{align} -
Step 3: Multiply the area of the base of the prism by the height of the prism to find the volume.
\begin{align} \text{Volume} & = \text{area of base}\times \text{height of prism} \\ & = 78\times 12 \\ & = \text{936 cm}^{3} \end{align} -
Step 4: Write the final answer and remember to show the correct units.
The volume of the cuboid is 936 cm .
You may calculate the volume of a prism in one step, using these formulae.
\begin{align} \text{Volume of a cuboid} &= \text{area of base} \times \text{height of cuboid}\\ &= l \times b \times h \end{align} \begin{align} \text{Volume of a cube} &= \text{area of base} \times \text{height of cube}\\ &= s \times s \times s \end{align}Exercise 13.13: Find the volume of cubes and cuboids
-
The picture below shows a cube. The length, width and height of the cube are 5 cm. Find the volume of the cube.

The volume of any prism is: . A cube is a prism with a square as its base.
\begin{array}{ll} {V}_\text{cube} & {= \text{area of base} \times \text{height of cube}} \\ & {= s \times s \times s}\\ & {= 5 \times 5 \times 5}\\ \text{V}_{cube} & {= \text{125 cm}^{3}} \\ \end{array}Answer: The volume of the cube is 125 cm .
-
The picture below shows a cube. The length, width and height of the cube are 30 mm. Find the volume of the cube.

\begin{array}{ll} {V}_\text{cube} & {= s \times s \times s}\\ & {= 30 \times 30 \times 30}\\ & {= \text{900} \times \text{30}} \\ \text{V}_{cube} & {= \text{27,000 mm}^{3}} \\ \end{array}
The volume of the cube is 27,000 mm .
-
The prism shown below is a cuboid. The height of the cuboid is 6 metres, the length is 12 metres and the breadth is 5 metres. Find the volume of the prism.
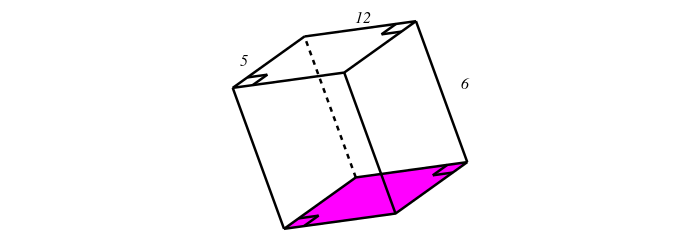
The volume of any prism is: . A cuboid is a prism with a rectangle as its base.
\begin{array}{ll} V_{\text{cuboid}} & {= \text{area of base} \times \text{height}} \\ & {= l_{\text{purple rectangle}} \times b_{\text{purple rectangle}}\times h} \\ & {= \text{12} \times \text{5} \times \text{6}} \\ & {= \text{360}\ {\text{m}^{3}}} \\ \end{array}The volume of the cuboid is 360 m .
-
The prism shown below is a cuboid. The height of the cuboid is 8 cm; the length and breadth are 10 cm and 4 cm respectively. Determine the volume of the cuboid.
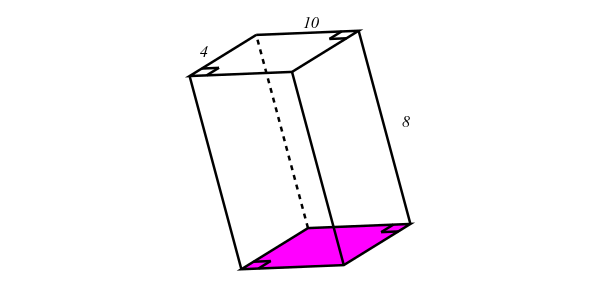
\begin{array}{ll} V_{\text{cuboid}} & {= l_{\text{purple rectangle}} \times b_{\text{purple rectangle}} \times h} \\ & {= \text{10} \times \text{4} \times \text{8}} \\ & {= \text{320}\ {\text{cm}^{3}}} \\ \end{array}
The volume of the cuboid is 320 cm .
-
The picture below shows a cube. The length, width and height of the cube are 4 metres. Find the volume of the cube.

\begin{array}{ll} {V}_\text{cube} & {= s \times s \times s}\\ & {= 4 \times 4 \times 4}\\ \text{V}_{cube} & {= \text{64 m}^{3}} \\ \end{array}
The volume of the cube is 64 m .
-
The prism below is a cuboid. The height of the cuboid is 12 mm, and the other dimensions of the cuboid are 11 mm and 8 mm. Find the volume of the cuboid.
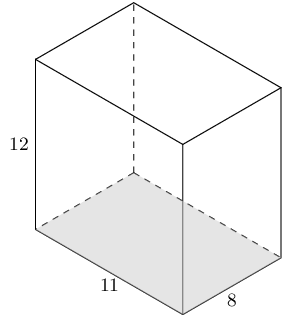
\begin{array}{ll} V_{\text{cuboid}} & = l \times b \times h \\ & = \text{11} \times \text{8} \times \text{12} \\ & = \text{1,056} \text{ mm}^{3} \end{array}
The volume of the cuboid is 1,056 mm .
13.7 Summary
- A three-dimensional (3D) object has three dimensions that we can measure: we can measure the length, the breadth (or width) and the height of the object.
- We use the main parts of a 3D object to describe its properties:
- A 3D object has faces. The faces can be flat or curved.
- The faces of a 3D object meet each other at an edge. The edge can be a straight line or a curve.
- The edges of a 3D object meet each other at a vertex. (Vertex is singular and vertices are plural.)
- The vertex at the top of a pyramid or a cone is called an apex.
Properties of 3D objects
| Name of 3D object | Number and shape of faces | Number of edges | Number of vertices |
|---|---|---|---|
| cube | 6 squares | 12 | 8 |
| cuboid | 3 pairs of equal rectangles = 6 rectangles | 12 | 8 |
| pyramid (square as base) | 1 square + 4 triangles = 5 faces | 8 | 5 |
| cone | 1 circle + 1 curved face = 2 faces | 1 | 1 |
| cylinder | 2 circles + 1 curved face = 3 faces | 2 | 0 |
| sphere | 1 curved face | 0 | 0 |
- Volume is the amount of space that an object takes up. It is measured in cubic units.
- The volume of a prism is calculated using the formula
- A cube is a prism. The formula for the volume of a cube is
- A cuboid is a prism. The formula for the volume of a cuboid is
