Chapter 12: Angles
In this chapter you will work with angles in different 2D shapes.
An angle is the amount of turn between two straight lines that have a common end point. The common end point is called the vertex of the angle.
The size of an angle does not depend on the length of the arms. The size of the angle depends on the amount of turn between the two arms.
In the diagram below, both angles have the same size.
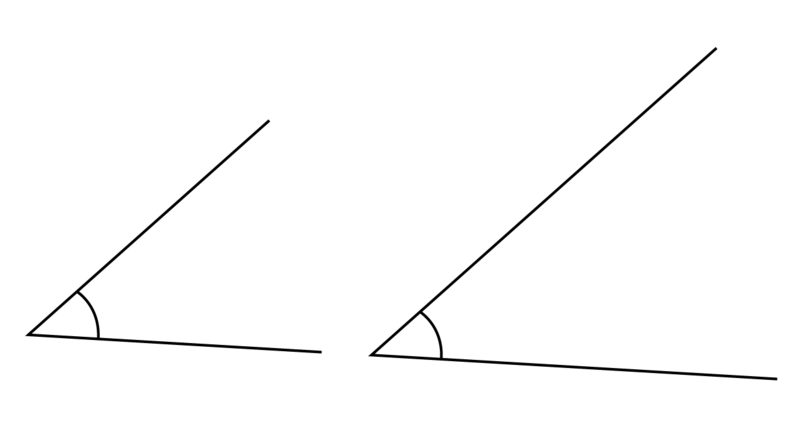
angle An angle is the amount of turn between two straight lines that have a common end point
vertex The vertex of an angle is common end point where the two arms of the angle meet.
12.1 Sum of angles in polygons
A 2D shape has interior angles on the inside of the shape, as well as exterior angles on the outside of a shape.
interior angle Interior angles are the angles formed formed by the sides of a shape, on the inside of the shape.
exterior angle Exterior angles are outside the shape. They are created by extending one of the sides of the shape. The side of the shape and the extension must form a straight line.
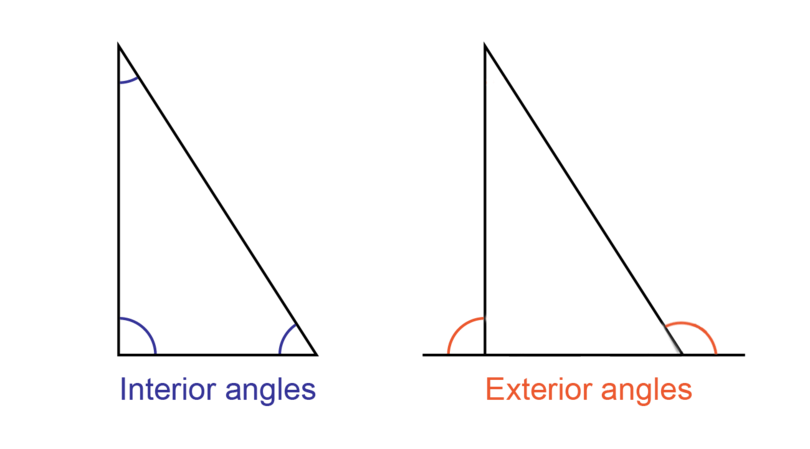
In this chapter you will focus on the sum of the interior angles of different polygons.
Sum of interior angles of a triangle
A triangle is a polygon with three sides.
Here is an activity for you to do:
Draw a big triangle on a sheet of paper, with angles of any size. Label the angles on the inside of the triangle as shown below. Cut out the triangle.

Tear or cut the triangle apart so that you have the three angles on three separate pieces of paper. Arrange the three angles next to each other. What do you notice?

The three angles of the triangle form a straight line. This means that the interior angles of a triangle add up to .
We write:
In geometry we always give reasons for our answers, so we add the reason between brackets:
Scalene triangles
One of the types of triangles we will work with is the scalene triangle. In a scalene triangle, all the interior angles are different in size, and all the sides are different in size.
As for any other triangle, the interior angles of a scalene triangle add up to .
scalene triangle A scalene triangle has three unequal angles and three unequal sides.
Worked example 12.1: Calculating an interior angle of a scalene triangle
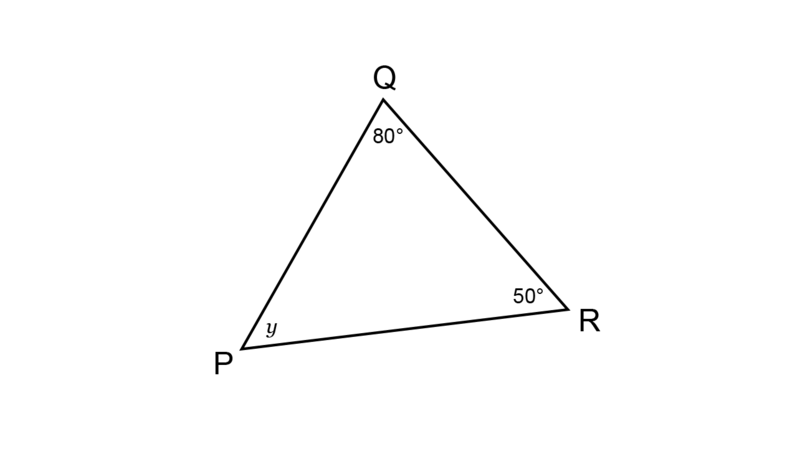
Determine the size of , giving a reason for your answer.
-
Step 1:Think of the geometric statement or fact that you will use, and write it down. Give the reasons between brackets.
-
Step 2: Substitute the given values and variables from the diagram into your statement.
\begin{align} \hat {P}+ \hat {Q} + \hat {R} &= 180^{\circ} \quad (\angle \text{ sum in } \triangle) \\ y + 50^{\circ} + 80^{\circ} & = 180^{\circ}\\ \end{align} -
Step 3: Solve the equation.
\begin{align} \hat {P} + \hat {Q} + \hat {R}& = 180^{\circ} \quad (\angle \text{ sum in } \triangle) \\ y + 50^{\circ} + 80^{\circ} & = 180^{\circ}\\ y + 130^{\circ} & = 180^{\circ} \\ y + 130^{\circ} - 130^{\circ} & = 180^{\circ} - 130^{\circ} \\ \therefore y & = 50^{\circ} \\ \end{align} -
Step 4: Check your solution.
A mental calculation will show that the sum of the three interior angles of adds up to :
\begin {align} \hat {P}+ \hat {Q} + \hat {R} & = 50^{\circ} + 50^{\circ} + 80^{\circ}\\ &= 180^{\circ}\\ \end {align}
Isosceles triangles
An isosceles triangle has two equal sides. As for all other triangles, all the interior angles of an isosceles triangle add up to .
We need to know two geometry facts about isosceles triangles:
-
If two sides of a triangle are equal, then the angles opposite those sides will be equal.
In , the two sides and are marked equal.
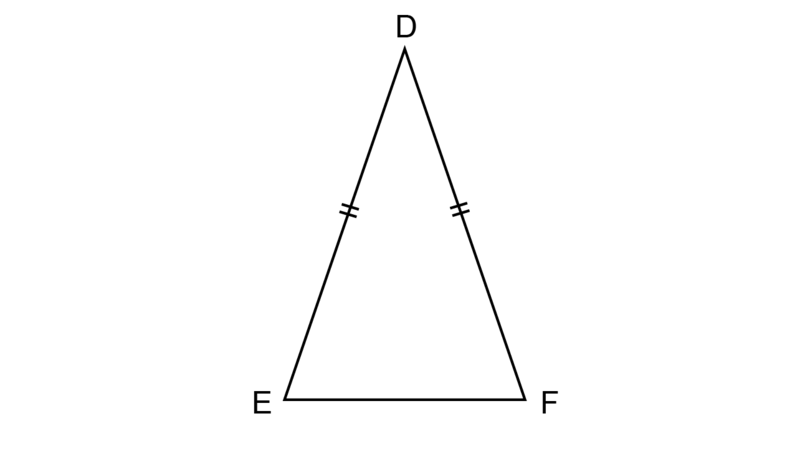
This means we can write the following geometric statement with its reason:
-
If two angles in a triangle are equal, then the sides opposite those angles will be equal.
In , the two angles and are marked equal.
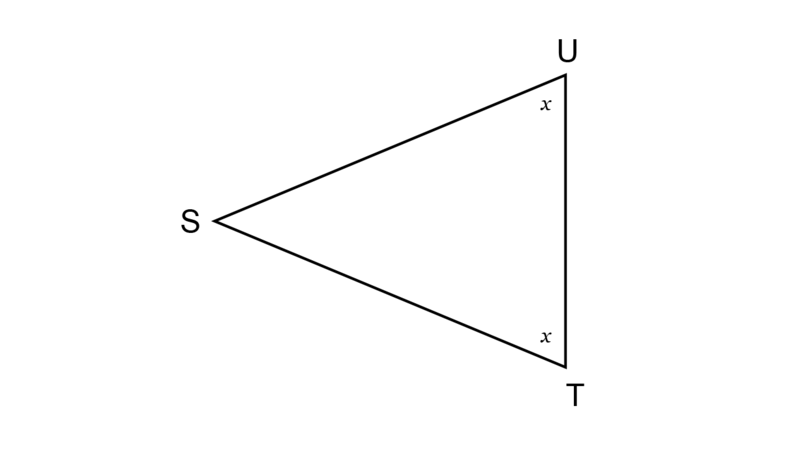
This means we can write the following geometric statement with its reason:
isosceles triangle An isosceles triangle has two equal sides. The angles opposite the equal sides are equal.
Worked example 12.2: Calculating interior angles of an isosceles triangle
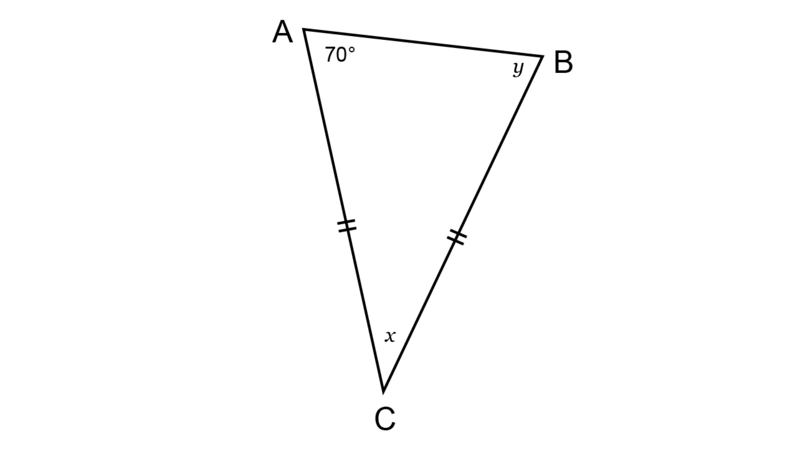
Determine the values of and , giving reasons for your answer.
-
Step 1: Always begin a solution with a geometric statement and a reason.
The information on the diagram shows that = .
So, the angles opposite these sides will be equal.

Write down:
-
Step 2: Determine the value of .
\begin{align} {\hat {B}} &{= \hat {A} \quad (\angle \text{s opp equal sides}) } \\ {\therefore y} & {= 70^{\circ}}\\ \end {align} -
Step 3: Determine the value of .
\begin{align} {\hat {A} + \hat {B} + \hat {C}} & { = 180^{\circ} \quad (\angle \text{ sum in } \triangle) } \\ {70^{\circ} + 70^{\circ} + x} & {= 180^{\circ}}\\ {x + 140^{\circ}} & {= 180^{\circ}} \\ {x + 140^{\circ} - 140^{\circ}} & {= 180^{\circ} - 140^{\circ}} \\ {\therefore x} & {= 40^{\circ}} \\ \end{align} -
Step 4: Check your solution.
A mental calculation will show that the sum of the three interior angles of adds up to :
\begin{align} \hat {A} + \hat {B} + \hat {C} & = 70^{\circ} + 70^{\circ} + 40^{\circ} \\ &= 180^{\circ} \\ \end{align}
Summary of the properties of triangles
- The three angles of any triangle always always add up to .
- A scalene triangle has three angles of different sizes.
- An isosceles triangle has two equal sides. The two angles opposite the equal sides are equal.
- An equilateral triangle has three equal sides and three equal angles. Each angle is equal to .
- A right-angled triangle has one angle of .
Exercise 12.1: Find the size of angles of a triangle
-
Determine the value of , giving a reason for your answer.
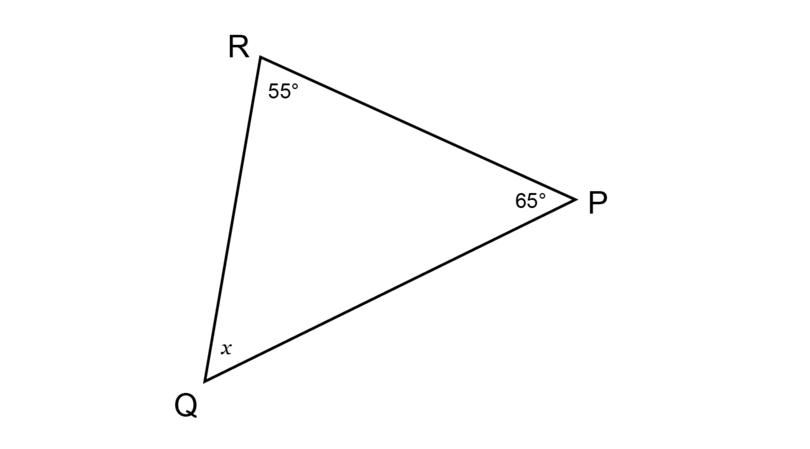
\begin{align} \hat {Q} + \hat {R} + \hat {P} & = 180^{\circ} \quad (\angle \text{ sum in } \triangle) \\ x + 55^{\circ} + 65^{\circ} & = 180^{\circ} \\ x + 120^{\circ} & = 180^{\circ} \\ x + 120^{\circ} - 120^{\circ} & = 180^{\circ} - 120^{\circ} \\ \therefore x & = 60^{\circ} \\ \end{align}
-
Determine the value of , giving a reason for your answer.
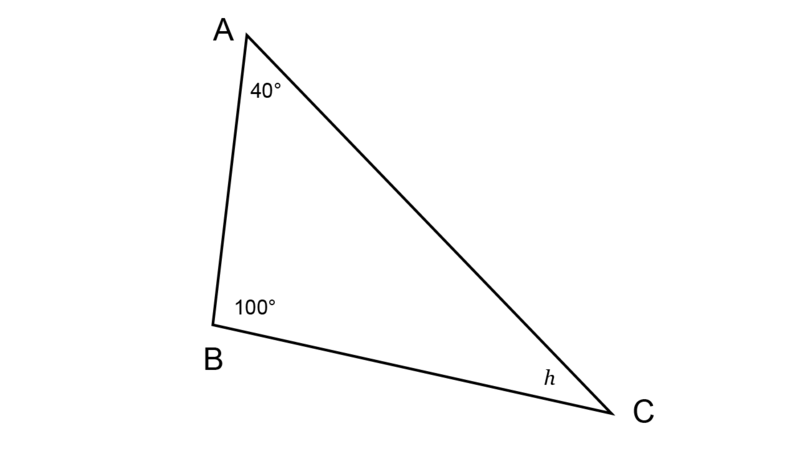
\begin{align} \hat {A} + \hat {B} + \hat {C} & = 180^{\circ} \quad (\angle \text{ sum in } \triangle) \\ 40^{\circ} + 100^{\circ} + h & = 180^{\circ} \\ h + 140^{\circ} & = 180^{\circ} \\ h + 140^{\circ} - 140^{\circ} & = 180^{\circ} - 140^{\circ} \\ \therefore h & = 40^{\circ} \\ \end{align}
-
In the triangle below, the interior angles are given as = , = and = . Calculate the size of the missing angle represented by .
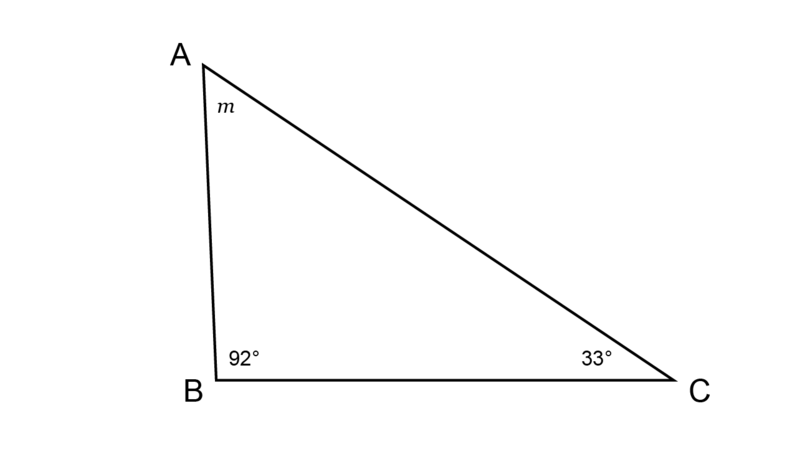
\begin{align} \hat {A} + \hat {B} + \hat {C} & = 180^{\circ} \quad (\angle \text{ sum in } \triangle) \\ 33^{\circ} + m + 92^{\circ} + h & = 180^{\circ} \\ m + 125^{\circ} & = 180^{\circ} \\ m + 125^{\circ} - 125^{\circ} & = 180^{\circ} - 125^{\circ} \\ \therefore m & = 55^{\circ} \\ \end{align}
-
Find the value of in the diagram below, giving reasons for your answer.
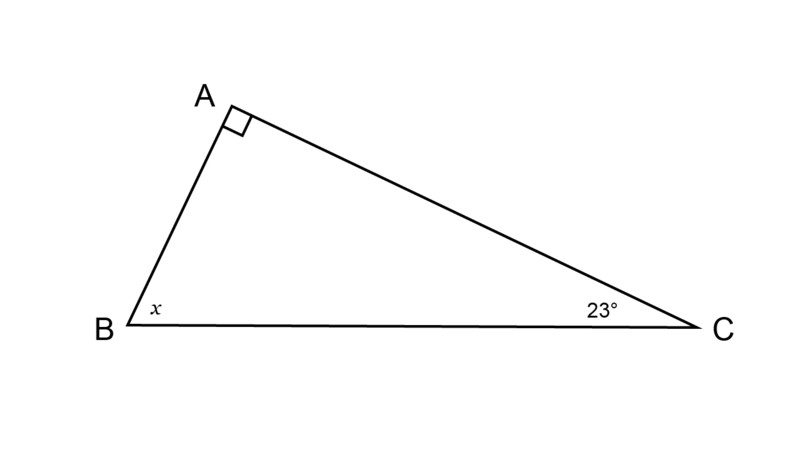
\begin{align} \hat {A} + \hat {B} + \hat {C} & = 180^{\circ} \quad (\angle \text{ sum in } \triangle) \\ 90^{\circ} + x + 23^{\circ} & = 180^{\circ} \\ x + 113^{\circ} & = 180^{\circ} \\ x + 113^{\circ} - 113^{\circ} & = 180^{\circ} - 113^{\circ} \\ \therefore x & = 67^{\circ} \\ \end{align}
-
Find the value of in the diagram below, giving reasons for your answer.
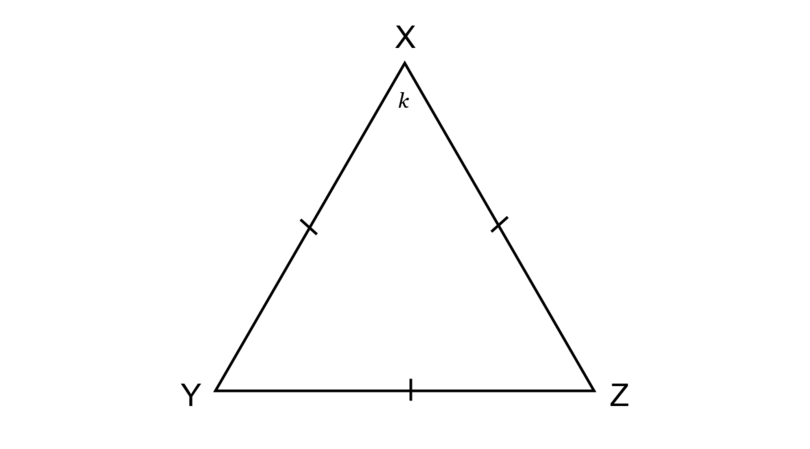
All three sides are marked equal, so is an equilateral triangle
\begin{align} k &= 180^{\circ} \div 3 \quad (\angle \text{s in equilateral } \triangle) \\ & = 60^{\circ} \\ \end{align} -
In the triangle below = . It is also given that = . Calculate the size of the missing angle represented by .
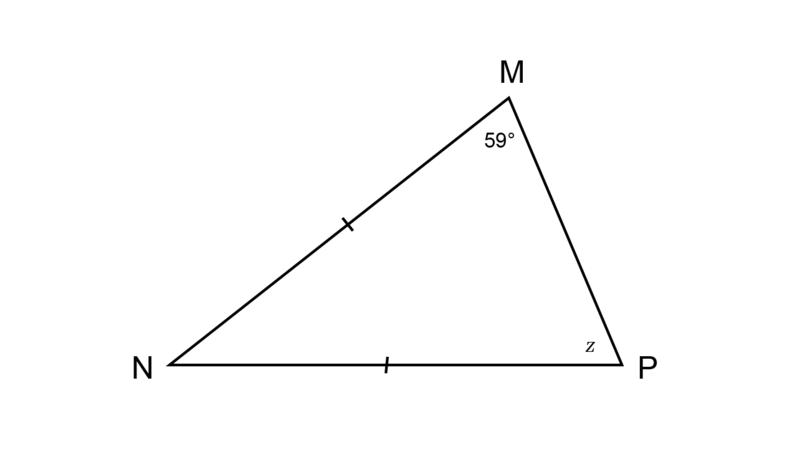
\begin{align} \hat {P} & = \hat {M} \quad (\angle s \text{ opp equal sides })\\ \therefore z & = 59^{\circ}\\ \end{align}
-
Determine the value of in the diagram below, giving reasons for your answer.

\begin{align} \hat {J} + \hat {K} + \hat {L} & = 180^{\circ} \quad (\angle \text{ sum in} \triangle) \\ 47^{\circ} + 47^{\circ} + y & = 180^{\circ} \\ y + 94^{\circ} & = 180^{\circ} \\ y + 94^{\circ} - 94^{\circ} & = 180^{\circ} - 94^{\circ} \\ \therefore y & = 86^{\circ} \\ \end{align}
-
Determine the value of in the diagram below, giving a reason for your answer.
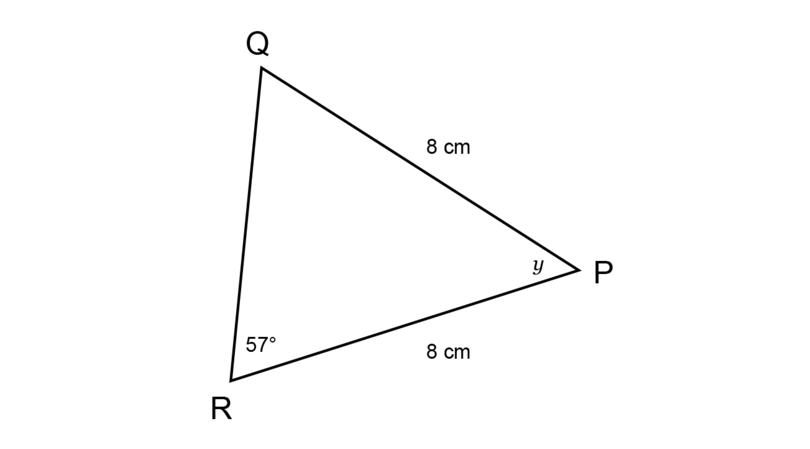
The information on the diagram shows that = . So, the angles opposite these sides will be equal.
\begin{align} \hat {Q} &= \hat {R} \quad (\angle \text{s opp equal sides}) \\ \therefore \hat {Q} &= 57^{\circ} \\ \hat {P} + \hat {Q} + \hat {R} & = 180^{\circ} (\angle \text{ sum in } \triangle) \\ y + 57^{\circ} + 57^{\circ} & = 180^{\circ} \\ y + 114^{\circ} & = 180^{\circ} \\ y + 114^{\circ} - 114^{\circ} & = 180^{\circ} - 114^{\circ} \\ \therefore y & = 66^{\circ} \\ \end{align}
-
Determine the value of in the diagram below, giving reasons for all statements.
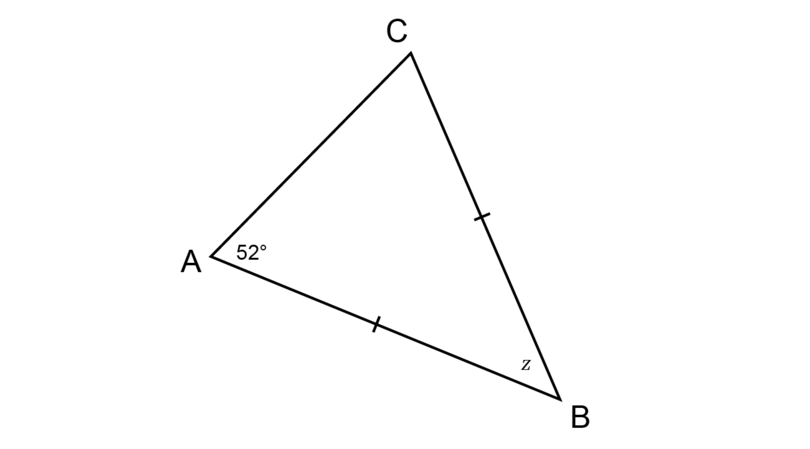
If two sides of a triangle are equal, then the angles opposite those sides will be equal.
\begin{align} \hat {C} & = \hat {A} \quad (\angle \text{s opp equal sides}) \\ \therefore \hat {C} & = 52^{\circ}\\ \hat {A} + \hat {B} + \hat {C} & = 180^{\circ} (\angle \text{ sum in } \triangle) \\ 52^{\circ} + z + 52^{\circ} & = 180^{\circ} \\ z + 104^{\circ} & = 180^{\circ} \\ z + 104^{\circ} - 104^{\circ} & = 180^{\circ} - 104^{\circ} \\ \therefore z & = 76^{\circ} \\ \end{align}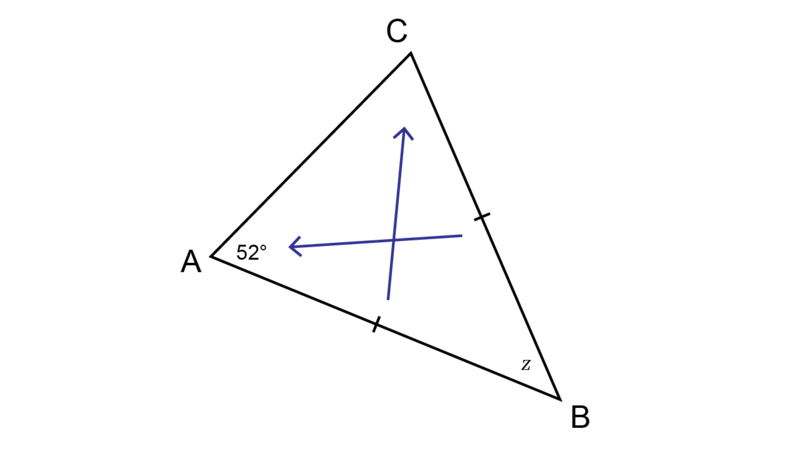
Sum of interior angles of a quadrilateral
We are also going to look at the properties of the interior angles of quadrilaterals, so that we can find missing angles.
A quadrilateral is a flat shape with four straight sides and four angles. Examples of quadrilaterals are squares, rectangles, rhombuses, parallelograms and kites.
quadrilateral A quadrilateral is a flat shape with four straight sides and four angles.
We know that a rectangle has four right angles. This means that the sum of the interior angles of a rectangle is .
So, the sum of the interior angles of a rectangle is .
Similarly, the sum of the interior angles of a square will also be .
What about other quadrilaterals?
For example, what is the sum of the interior angles of quadrilateral given below?
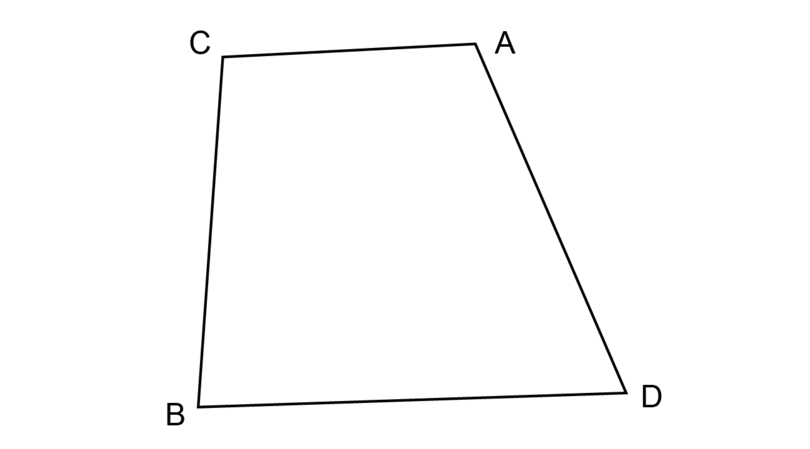
You can divide quadrilateral into two triangles:
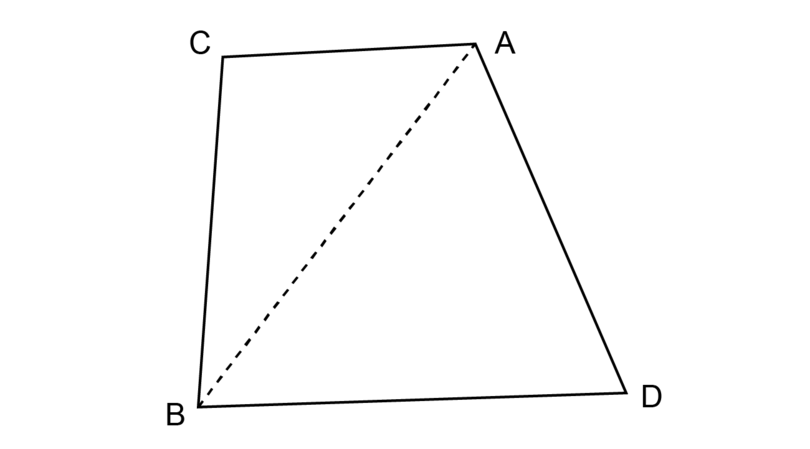
-
The sum of the interior angles of = .
-
The sum of the interior angles of = .
Therefore, the sum of the interior angles of quadrilateral = .
Any quadrilateral can be divided into two triangles. So, the sum of the interior angles of a quadrilateral is equal to the sum of the interior angles of two triangles.
\begin{align} \text{Sum of interior angles of quadrilateral} &= \text {sum of interior angles of two triangles}\\ &= 2 \times 180^{\circ}\\ &= 360^{\circ}\ \end{align}
Worked example 12.3: Calculating interior angles of a quadrilateral
In quadrilateral below, = , = , = and = .
Determine the value of , giving a reason for your answer.
-
Step 1: Remember that the interior angles of a quadrilateral add up to .
You do not need to show this step in your working out. It is just here so that you can see where the fact comes from.
-
Step 2: Write down a geometric statement with a reason.
-
Step 3: Solve the equation.
\begin{align} x + 110^{\circ} + 104^{\circ} + 47^{\circ} & = 360^{\circ} \quad ( \text{sum of } \angle \text{s in quad} )\\ x + 261^{\circ} & = 360^{\circ} \\ x + 261^{\circ} - 261^{\circ} & = 360^{\circ} - 261^{\circ} \\ \therefore x & = 99^{\circ} \\ \end{align}
Exercise 12.2: Calculate interior angles of a quadrilateral
-
Draw the following quadrilaterals: a square, a parallelogram and a kite.
Divide each quadrilateral into two triangles.
What conclusion can you make about the sum of the interior angles of a quadrilateral?
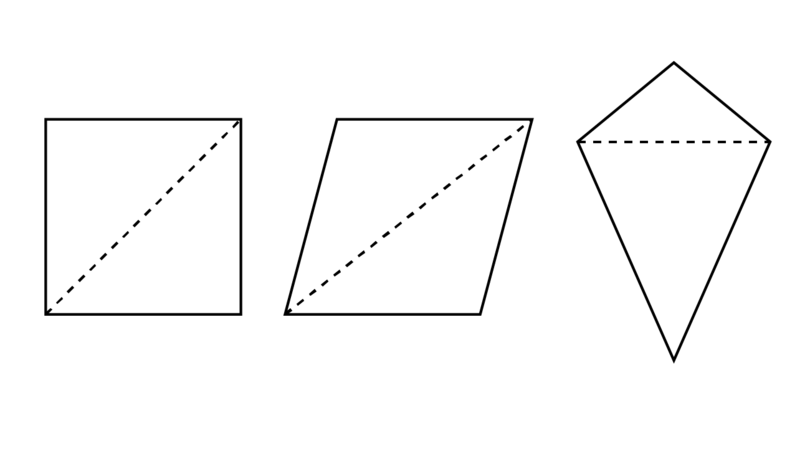
Conclusion: A square, a parallelogram and a kite are all quadrilaterals. They can all be dvided into two triangles. Therefore, the sum of the interior angles of a quadrilateral is .
-
In quadrilateral below, = , = , = and = .
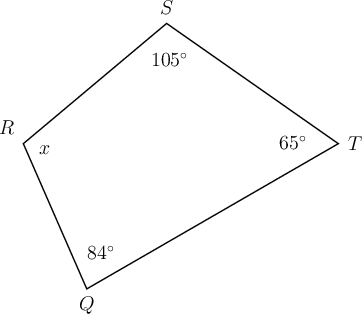
Determine the value of , giving a reason for your answer.
\begin{align} 84^{\circ} + x + 105^{\circ} + 65^{\circ} & = 360^{\circ} \quad ( \text{sum of }\angle \text{s in quad} ) \\ x + 254^{\circ} & = 360^{\circ} \\ x + 254^{\circ} - 254^{\circ} & = 360^{\circ} - 254^{\circ} \\ \therefore x & = 106^{\circ} \\ \end{align}
-
In quadrilateral below, = , = , = and = .
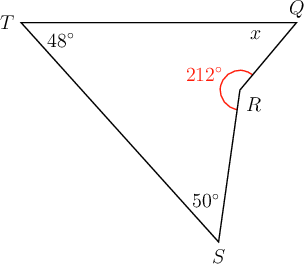
Determine the value of , giving a reason for your answer.
\begin{align} x + 212^{\circ} + 50^{\circ} + 48^{\circ} & = 360^{\circ} \quad ( \text{sum of } \angle \text{s in quad} ) \\ x + 310^{\circ} & = 360^{\circ} \\ x + 310^{\circ} - 310^{\circ} & = 360^{\circ} - 310^{\circ} \\ \therefore x & = 50^{\circ} \\ \end{align}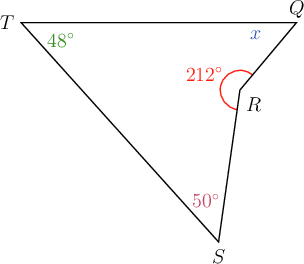
- In quadrilateral
:
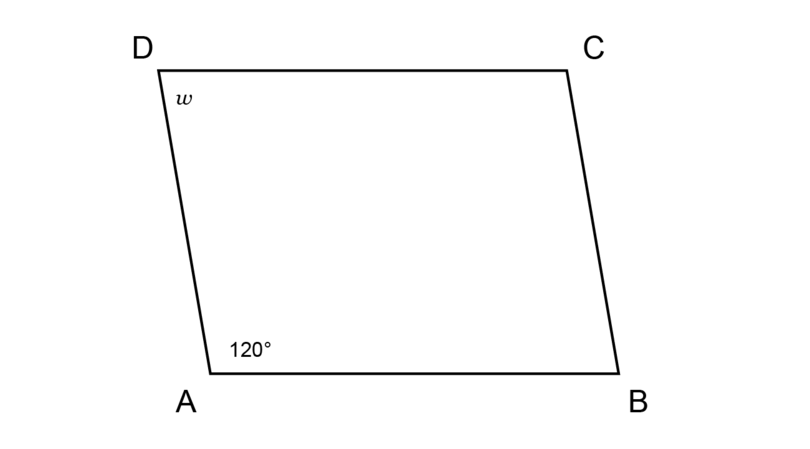
- What type of quadrilateral is ?
has two pairs of parallel sides, so is a parallelogram.
- Find the value of , giving reasons for your answer.
In a parallelogram the opposite angles are equal.

So, =
\begin{align} \hat {A} + \hat {B} + \hat {C} + \hat {D} & = 360^{\circ} \quad ( \text{sum of } \angle \text{s in quad} ) \\\ 120^{\circ} + \hat {B} + 120^{\circ} + \hat {D} & = 360^{\circ} \\ \hat {B} + \hat {D} + 240^{\circ} & = 360^{\circ} \\ \hat {B} + \hat {D} + 240^{\circ} - 240^{\circ} & = 360^{\circ} - 240^{\circ} \\ \hat {B} + \hat {D} & = 120^{\circ} \\ \hat {B} & = \hat {D} (\text{opp } \angle \text{s of parallelogram}) \\ \therefore \hat {D} & = 120^{\circ} \div 2 \\ &= 60^{\circ} \\ \therefore w & = 60^{\circ} \\ \end{align}
Sum of interior angles of other polygons
A polygon is a closed shape made of straight lines. In a closed shape, the sides are made using one line that follows another line until you get back to where you started, and there are no openings.
polygon A polygon is a closed shape made of straight lines.
We name polygons by the number of sides they have.
| Number of sides | Name of polygon |
|---|---|
| 3 | triangle |
| 4 | quadrilateral |
| 5 | pentagon |
| 6 | hexagon |
| 7 | heptagon |
| 8 | octagon |
| 9 | nonagon |
| 10 | decagon |
We can determine the sum of the interior angles of any polygon by dividing the polygon into triangles.
A pentagon is a polygon with five sides.

Draw lines from one vertex of the pentagon and divide the pentagon into triangles, as shown below:

The pentagon can be divided into three triangles.
\begin{align} \text{Sum of interior angles of pentagon} & = \text{ sum of interior angles of three } \triangle \text{s} \\ & = 3 \times 180^{\circ} \\ & = 540^{\circ}\\ \end{align}Worked example 12.4: Finding the sum of the interior angles of a polygon by dividing into triangles
Determine the sum of the interior angles of the polygon by dividing it into triangles.
-
Step 1: Count the number of sides and identify the polygon.
This polygon has 6 sides, so it is a hexagon.
-
Step 2: Draw lines from one vertex and divide the polygon into triangles. Write down the number of triangles.
The polygon can be divided into four triangles.
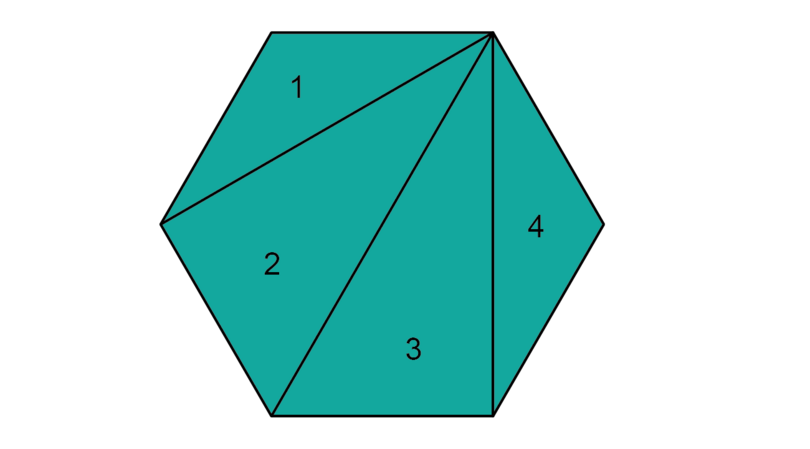
-
Step 3: Determine the sum of the interior angles of the polygon.
\begin{align} \text{Sum of interior angles of hexagon} & = \text{ sum of interior angles of four } \triangle \text{s} \\ & = 4 \times 180^{\circ} \\ & = 720^{\circ}\\ \end{align}
We have seen that:
- a polygon with 4 sides can be divided into 2 triangles
- a polygon with 5 sides can be divided into 3 triangles
- a polygon with 6 sides can be divided into 4 triangles.
This pattern will continue, so:
- a polygon with 7 sides can be divided into 5 triangles
- a polygon with 8 sides can be divided into 6 triangles
- a polygon with 9 sides can be divided into 7 triangles
- a polygon with 10 sides can be divided into 8 triangles, and so on.
There is a pattern when we divide a polygon into triangles: the number of triangles is always 2 less than the number of sides of the polygon.
The sum of the interior angles of a triangles is .
= + .
So, we can also say that is the sum of two right angles.
A table shows the pattern very clearly:
| Number of sides | Number of triangles | Number of right angles |
|---|---|---|
| 4 | 2 | 4 |
| 5 | 3 | 6 |
| 6 | 4 | 8 |
| 7 | 5 | 10 |
| 8 | 6 | 12 |
| 9 | 7 | 14 |
| 10 | 8 | 16 |
This means we can use a formula to calculate the sum of the interior angles of a polygon:
A right angle is , so we can write:
Worked example 12.5: Finding the sum of the interior angles of a polygon using a formula
Identify the polygon below and determine the sum of the interior angles by using a formula.
-
Step 1: Count the number of sides and identify the polygon.
The diagram in this question shows a polygon with 5 sides. This polygon is called a pentagon.
-
Step 2: Write down the formula to determine the sum of the interior angles of the polygon.
Sum of interior angles =
-
Step 3: Substitute the correct value for .
A pentagon has 5 sides, so .
-
Step 4: Solve the equation.
\begin{align} \text{Sum of interior } \angle \text{s of pentagon} & = (2 \times 5 - 4) \text { right angles} \\ & = (10 - 4) \text { right angles} \\ & = 6 \times \text {right angles} \\ & = 6 \times 90^{\circ} \\ \therefore \text{Sum of interior } \angle \text{s of pentagon} & = 540^{\circ} \\ \end{align}So, this polygon is a pentagon and the sum of the interior angles of a pentagon is .
Keep the rules of BODMAS in mind when you have to simplify the following calculation:
- You have to multiply first: =
- Subtraction follows after multiplication: =
Exercise 12.3: Find the sum of interior angles of polygons
-
Identify the polygon below and determine the sum of the interior angles by using the formula.

The diagram shows a polygon with 6 sides. This polygon is called a hexagon.
A hexagon has 6 sides, so .
\begin{align} \text{Sum of interior } \angle \text{s of hexagon} & = (2 \times 6 - 4) \text { right angles} \\ & = (12 - 4) \text { right angles} \\ & = 8 \times \text {right angles} \\ & = 8 \times 90^{\circ} \\ \therefore \text{Sum of interior } \angle \text{s of hexagon} & = 720^{\circ} \\ \end{align} -
Identify the polygon, and determine the sum of the interior angles, using a formula.
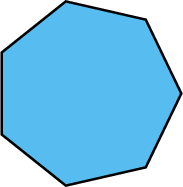
A polygon with 7 sides is called a heptagon.
\begin{align} \text{Sum of interior } \angle \text{s of heptagon} & = (2 \times 7 - 4) \text { right angles} \\ & = (14 - 4) \text { right angles} \\ & = 10 \times \text {right angles} \\ & = 10 \times 90^{\circ} \\ \therefore \text{Sum of interior } \angle \text{s of heptagon} & = 900^{\circ} \\ \end{align} -
Identify the polygon and use the formula to determine the sum of the interior angles.

A polygon with 8 sides is called an octagon.
\begin{align} \text{Sum of interior } \angle \text{s of octagon} & = (2 \times 8 - 4) \text { right angles} \\ & = (16 - 4) \text { right angles} \\ & = 12 \times \text {right angles} \\ & = 12 \times 90^{\circ} \\ \therefore \text{Sum of interior } \angle \text{s of octagon} & = 1,080^{\circ} \\ \end{align} -
Identify the polygon and use the formula to determine the sum of the interior angles.

A polygon with 10 sides is called a decagon.
\begin{align} \text{Sum of interior } \angle \text{s of decagon} & = (2 \times 10 - 4) \text { right angles} \\ & = (20 - 4) \text { right angles} \\ & = 16 \times \text {right angles} \\ & = 16 \times 90^{\circ} \\ \therefore \text{Sum of interior } \angle \text{s of decagon} & = 1,440^{\circ} \\ \end{align} -
Identify the polygon and use the formula to determine the sum of the interior angles.

A polygon with 4 sides is called a quadrilateral.
\begin{align} \text{Sum of interior } \angle \text{s of quadrilateral} & = (2 \times 4 - 4) \text { right angles} \\ & = (8 - 4) \text { right angles} \\ & = 4 \times \text {right angles} \\ & = 4 \times 90^{\circ} \\ \therefore \text{Sum of interior } \angle \text{s of quadrilateral} & = 360^{\circ} \\ \end{align}
12.2 Angles of elevation and depression
In this section you are going to learn about two new types of angles. These angles depend on the way that we look at things.
Recognising angles of elevation and angles of depression
Angles of elevation and angles of depression are angles that are formed by looking upwards or downwards from a horizontal line.
If the line of sight is upward from the horizontal line, the angle is an angle of elevation. For example, when you sit outside and look up at a bird, the position of the bird is higher than your position. So you are looking at the bird at an angle of elevation.

If the line of sight is downward from the horizontal line, the angle is an angle of depression. For example, when you stand on a cliff and look down at a friend on the road below, the position of your friend is lower than your position. So you are looking at an angle of depression.

It is important to realise that the angle of elevation is equal to the angle of depression if the two angles are taking place between the same horizontal lines. This is because the horizontal lines are parallel. When two parallel lines are intersected by a transversal, the alternate angles are equal.
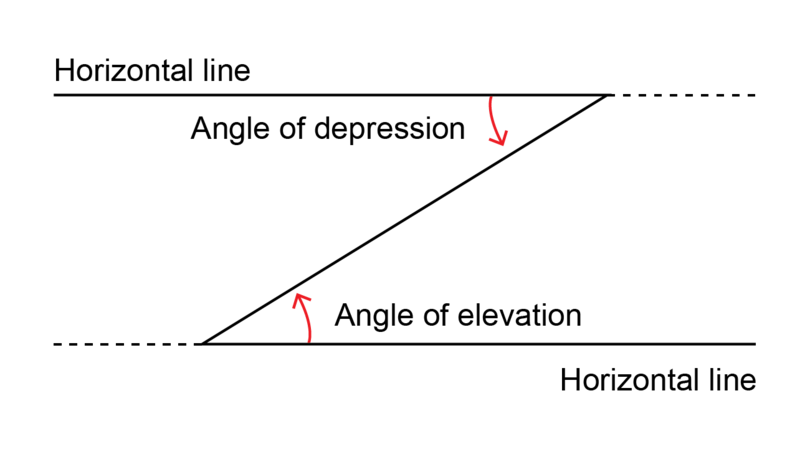
angle of elevation An angle of elevation is the angle formed when the line of sight is upward from a horizontal line.
angle of depression An angle of depression is the angle formed when the line of sight is downward from a horizontal line.
Worked example 12.6: Recognising angles of elevation and angles of depression
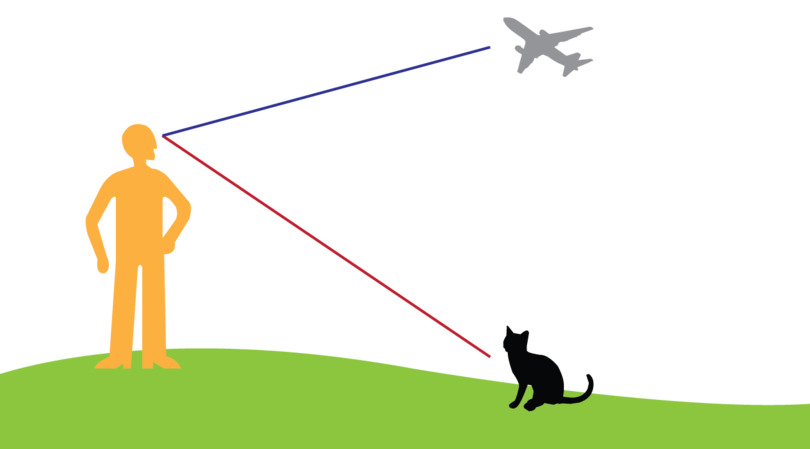
Wole is standing outside his house. He sees an aeroplane as well as a cat.
Show the angle of elevation and the angle of depression in the diagram.
-
Step 1: Draw the horizontal line.
Draw a horizontal line at the line of sight (from Wole's eyes).
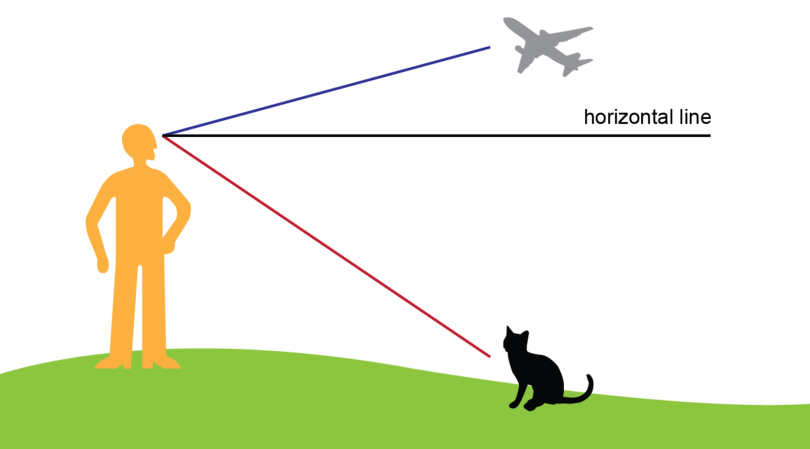
-
Step 2: Mark the angle of elevation.
An angle of elevation is formed when the line of sight is upward from the horizontal line.
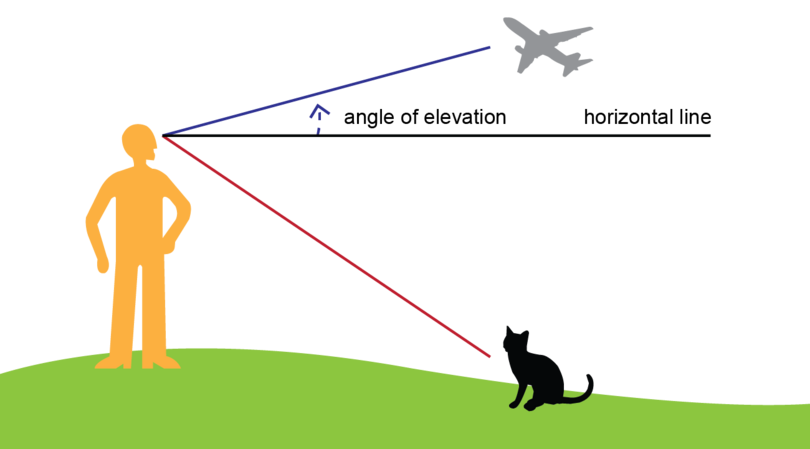
-
Step 3: Mark the angle of depression.
An angle of depression is formed when the line of sight is downward from the horizontal line.
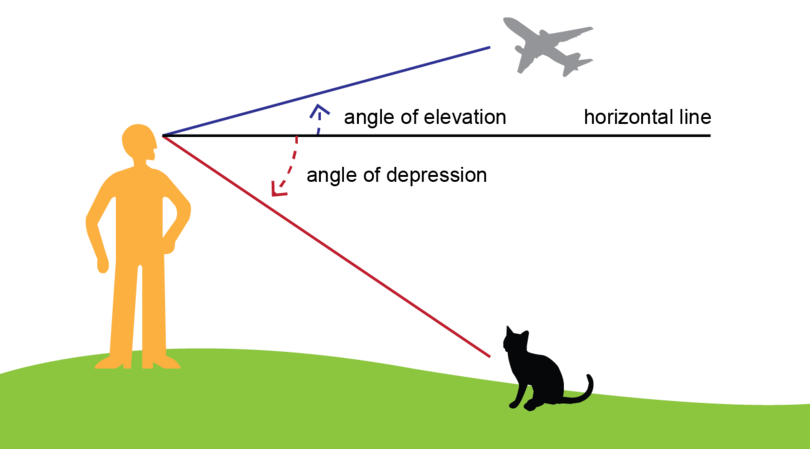
Exercise 12.4: Recognise angles of elevation and angles of depression
-
Yuwa is sitting outside the classroom. She looks at the top of flag pole.
Is the angle marked an angle of elevation or an angle of depression? Explain your answer.

The angle marked is an angle of elevation.
Yuwa is looking upwards from the horizontal line.
-
Habib is standing on a cliff next to a lake. He sees a fishing boat.
Is the angle marked an angle of elevation or an angle of depression? Explain your answer.

The angle marked is an angle of depression.
Habib is looking downwards from the horizontal line.
-
A bird is sitting at point on the roof of a building. Which angle in the diagram is an angle of depression? Which angle in the diagram is an angle of elevation?

is an angle of depression.
is an angle of elevation. -
In the diagram below is a tree. The angle of elevation from to is .
Which other angle in the diagram is also equal to ? Give a reason for your answer.

= .
Reason: because they are both horizontal lines.
If two parallel lines are intersected by a transversal, the alternate angles are equal.
12.3 Practical applications
It is not always possible to measure the actual size of an object, for example the height of a tall tree. Then we can make use of a scale drawing where we also include an angle of elevation.
We need to know what the ratio is in which we have to reduce (or enlarge) the real life object to do a scale drawing. This ratio is called the scale of the drawing.
For example, a scale of means that 1 unit on the scale drawing represents 5 units in real life.
scale drawing A scale drawing is a diagram of a real object where every measurement is reduced (or enlarged) in the same proportion.
scale The scale of a scale drawing tells us what ratio to use to reduce (or enlarge) the size of the real life object to make the scale drawing.
Worked example 12.7: Using scale in scale drawings
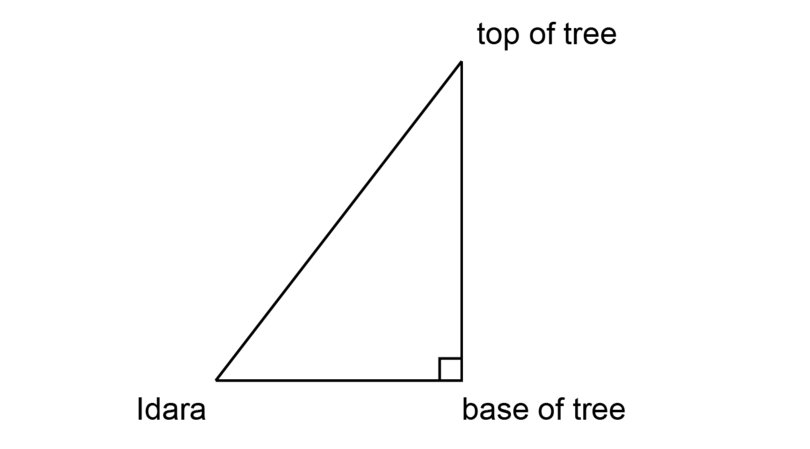
Idara wants to know the height of a tree that is standing across the road from her house. The tree is too high to measure, but she knows that the angle of elevation from the road to the top of the tree is . The distance between Idara and the base of the tree is 10 metres.
Make use of your knowledge of scale drawing and angles of elevation to calculate the height of the tree. Use a scale of .
-
Step 1: Fill in all the given information on a rough sketch.
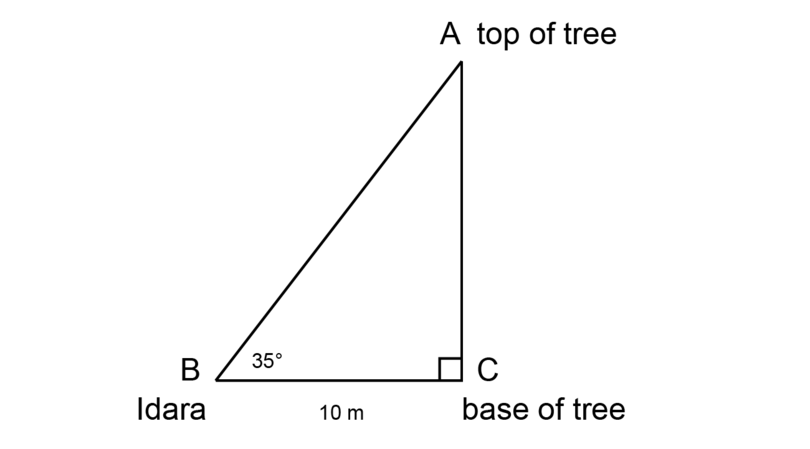
It is a good idea to label the vertices of the triangle. It is easier to work with a named triangle, for example , when you have to do calculations.
-
Step 2: Use the given scale to calculate the length of the line segment on the scale drawing.
1 metre = 100 cm, so 10 metres = 1,000 cm
\begin{align} \text {Length BC in real life} & = \text{1,000 cm}\\ \text {Length of BC on scale drawing} & = \text{1,000 cm} \div 100\\ &= \text{10 cm} \end{align} -
Step 3: Make an accurate scale drawing.
Use the following steps:
- Construct line segment = 10 cm.
- Construct = .
- Construct .
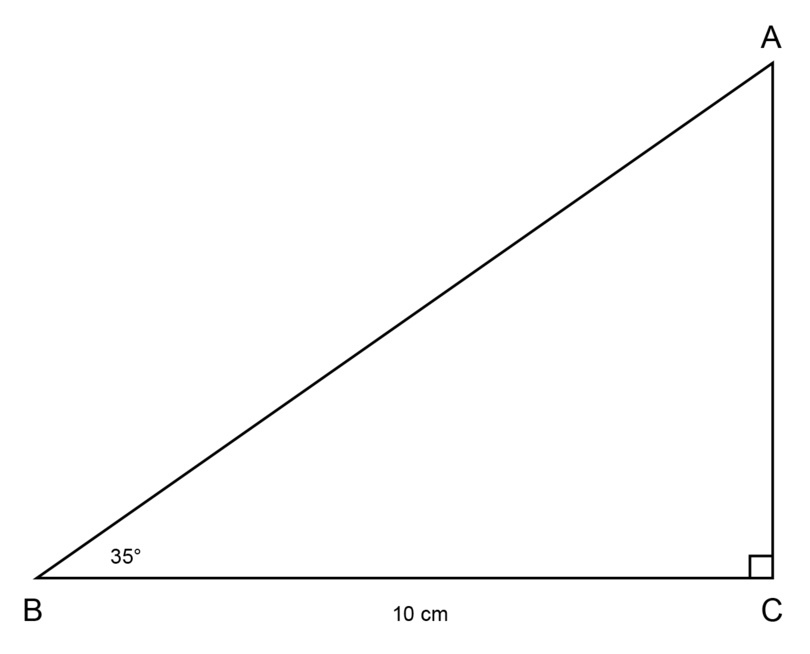
It is possible that the diagram given above does not display correctly on your device. The accurate scale drawing should have the given measurements.
-
Step 4: Measure the line segment representing the height of the tree.
Line segment represents the height of the tree.
= 7 cm
-
Step 5: Calculate the height of the tree in real life.
\begin{align} \text {Length of AC on scale drawing} & = \text{7 cm}\\ \text {Length of AC in real life} & = \text{7 cm} \times 100\\ &= \text{700 cm}\\ &= \text {7 metres} \end{align}The height of the tree is 7 metres.
When we do scale drawings, we have to measure the lengths of line segments on diagrams accurately. It is possible that the given diagrams do not display correctly on your device. If so, you will not be able to measure the lengths of the line segments as expected.
To assist you, the expected measurements are given in each question in the exercise below. You may use these measurements to do the necessary calculations.
Exercise 12.5: Use scale in scale drawings
-
The distance from where Uyai is standing to the foot of a pole is 420 cm. The angle of elevation from to the top of the pole is .

Make a scale drawing to determine the height of the pole. Use a scale of .
\begin{align} \text {Length AC in real life} & = \text{420 cm}\\ \text {Length of AC on scale drawing} & = \text{420 cm} \div 100\\ &= \text{4.2 cm} \end{align}
Construct a scale drawing, using the following steps:
- Construct = 4.2 cm.
- Construct = .
- Construct .

Measure the length of .
Expected measurement for : = 9 cm
\begin{align} \text {Length of BC on scale drawing} & = \text{9 cm}\\ \text {Length of BC in real life} & = \text{9 cm} \times 100\\ &= \text{900 cm}\\ &= \text {9 metres} \end{align}The height of the pole is 9 metres.
-
Yabani is standing on a bridge (point ). He looks downward at an angle of to his friend who is swimming in the river below (at point ). How far is his friend from him if the distance from to is 40 metres in real life?
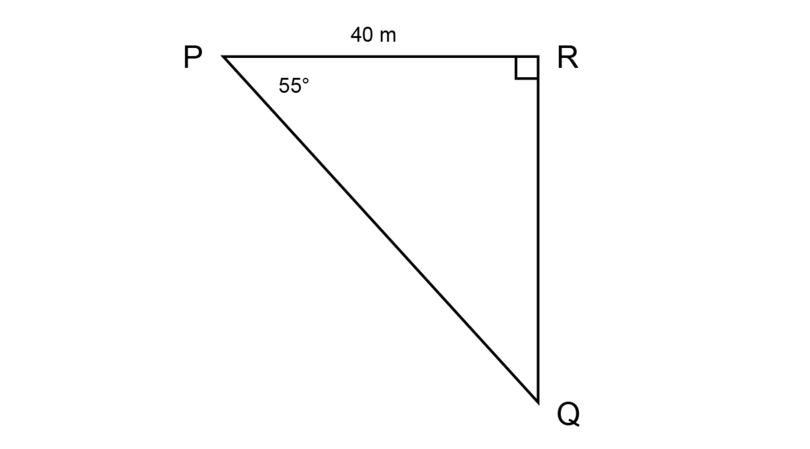
Draw a scale drawing, using a scale of .
1 metre = 100 cm, so 40 metres = 4,000 cm
\begin{align} \text {Length PR in real life} & = \text{4,000 cm}\\ \text {Length of PR on scale drawing} & = \text{4,000 cm} \div 1,000\\ &= \text{4 cm} \end{align}Construct a scale drawing, using the following steps:
- Construct = 4 cm.
- Construct = .
- Construct .
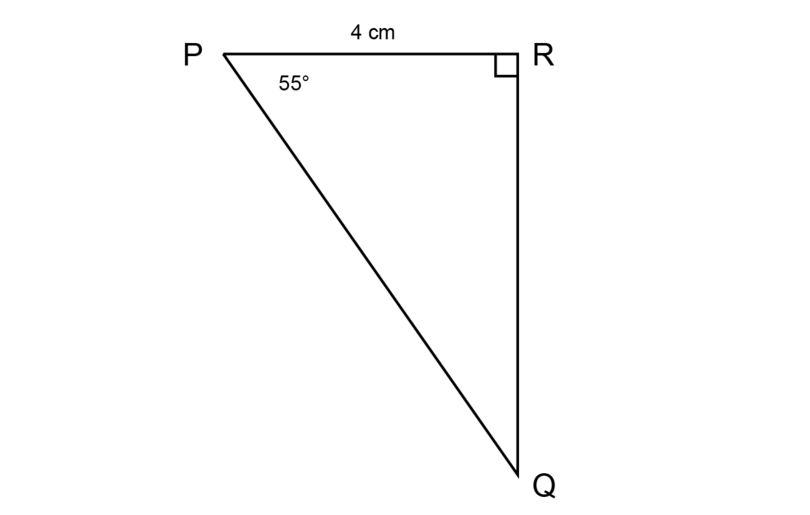
Measure the length of .
Expected measurement for : = 7 cm
\begin{align} \text {Length of PQ on scale drawing} & = \text{7 cm}\\ \text {Length of PQ in real life} & = \text{7 cm} \times 1,000\\ &= \text{7,000 cm}\\ &= \text {70 metres} \end{align}The distance between Yabani and his friend is 70 metres.
-
Two buildings are 20 metres apart from each other. The angles of elevation and depression from the roof of the one building are shown in the diagram below.
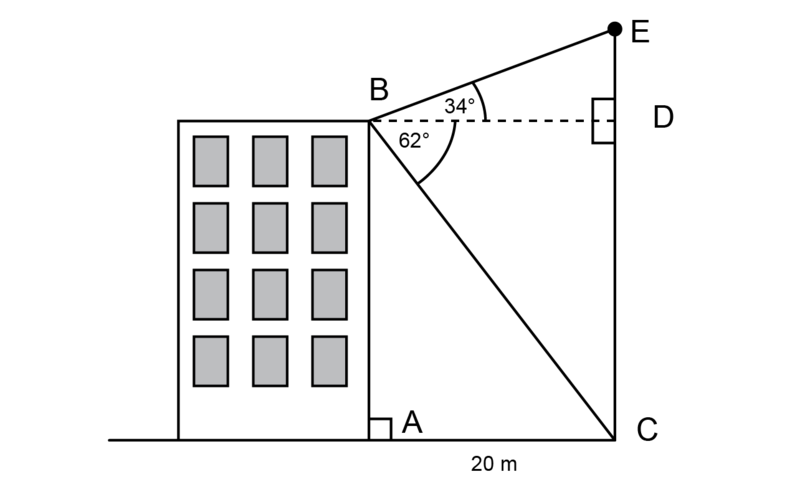
If is the height of the second building), make use of a scale drawing to determine this height. Use a scale of .
If the buildings are 20 metres apart, it means that = 20 m also.
1 metre = 100 cm, so 20 metres = 2,000 cm
\begin{align} \text {Length BD in real life} & = \text{2,000 cm}\\ \text {Length of BD on scale drawing} & = \text{2,000 cm} \div 400\\ &= \text{5 cm} \end{align}Construct a scale drawing of using the following steps:
- Construct = .
- Construct = .
- Construct = .
- Construct .
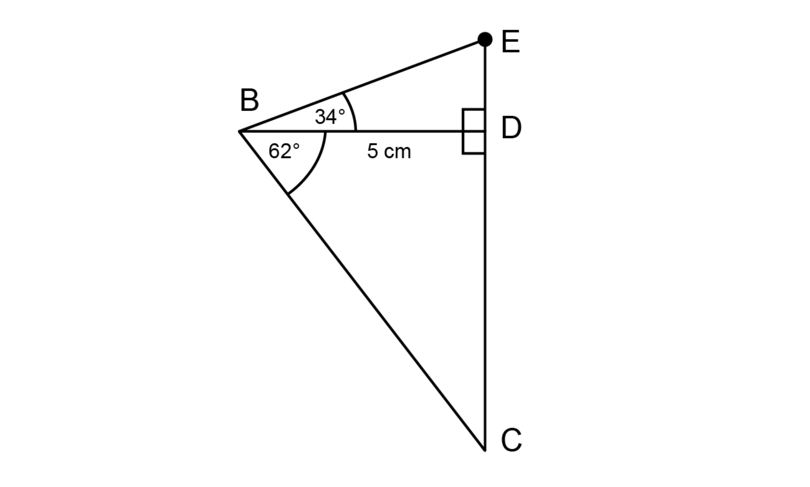
Measure the length of on the scale drawing.
Expected measurement for : = 12.7 cm
\begin{align} \text {Length of EC on scale drawing} & = \text{12.7 cm}\\ \text {Length of EC in real life} & = \text{12.7 cm} \times 400\\ &= \text{5,080 cm}\\ &= \text {50.8 metres} \end{align}The height of the second building is 50.8 metres.
12.4 Summary
- An angle is the amount of turn between two straight lines that have a common end point. The common end point is called the vertex of the angle.
- A 2D shape has interior angles as well as exterior angles.
- Interior angles are inside the shape.
- Exterior angles are outside the shape.
- The sum of the interior angles of a triangle is .
- The sum of the interior angles of a quadrilatral is .
- Polygons are named according to the number of sides they have:
| Number of sides | Name of polygon |
|---|---|
| 3 | triangle |
| 4 | quadrilateral |
| 5 | pentagon |
| 6 | hexagon |
| 7 | heptagon |
| 8 | octagon |
| 9 | nonagon |
| 10 | decagon |
- We can determine the sum of the interior angles of any polygon by dividing the polygon into triangles. This table shows the pattern:
| Number of sides | Number of triangles | Number of right angles |
|---|---|---|
| 3 | 1 | 2 |
| 4 | 2 | 4 |
| 5 | 3 | 6 |
| 6 | 4 | 8 |
| 7 | 5 | 10 |
| 8 | 6 | 12 |
| 9 | 7 | 14 |
| 10 | 8 | 16 |
- The formula to calculate the sum of the interior angles of a polygon is: sum of interior angles of a polygon with sides right angles
- An angle of elevation is the angle formed when the line of sight is upward from a horizontal line.
- An angle of depression is the angle formed when the line of sight is downward from a horizontal line.
- The angle of elevation is equal to the angle of depression, because the horizontal lines are parallel. When two parallel lines are intersected by a transversal, the alternate angles are equal.
- We can make use of a scale drawing and an angle of elevation or an angle of depression to solve practical problems.