Chapter 5: Multiplication and division
5.1 Multiplication and division of integers
Last year you learnt how to add and subtract integers. The set of integers is all the positive and negative whole numbers, including zero. You used a number line to represent integers.
- Numbers to the right of zero on the number line are called positive numbers. We represent them with or without a plus sign in front. For example, the positive number five may be written as or just .
- Numbers to the left of zero are called negative numbers. We always represent them with a minus sign in front. For example, the negative number three is written as .
- The number is neither positive nor negative.
integer The integers are the positive and negative whole numbers, including zero.
positive number Positive numbers are numbers that are larger than zero; they lie to the right of zero on a number line.
negative number Negative numbers are numbers that are smaller than zero; they lie to the left of zero on a number line.
Positive and negative numbers are sometimes called directed numbers. This is because the sign of the number (positive or negative) tells us in which direction from zero they appear on the number line.
directed number Directed numbers are positive and negative numbers. The sign of a directed number tells us in which direction from zero it lies on the number line.
In this section, you will learn how to multiply and divide directed numbers.
Multiplying directed numbers
From earlier grades you know that we can multiply numbers in any order. For example, and .
In Mathematics, the commutative laws of addition and multiplication state that the order in which we add or multiply numbers does not affect the answer. This means we can swap numbers around and still get the same answer.
From last year you know that multiplication may be seen as a form of addition. Therefore:
or
This means that you get a positive answer when you multiply two positive numbers:
We may use the same method to find out what happens when we multiply a positive number by a negative number or a negative number by a positive number.
or
Remember means we start at on the number line and count three units to the left. This brings us to .
This shows that you get a negative answer when you multiply two numbers with opposite signs:
It is a bit more complicated to explain what happens when we multiply two negative numbers. One way of thinking states that, for all the laws of Mathematics to work, we accept by convention that . Another way is to look at number patterns. This table shows multiplication by :
\begin{array}{|c|c|c|c|c|} \hline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline -2 & \times & & = & \newline \hline \end{array}Let's insert a number pattern in the middle column:
\begin{array}{|c|c|r|c|c|} \hline -2 & \times & +4 & = & \newline -2 & \times & +3 & = & \newline -2 & \times & +2 & = & \newline -2 & \times & +1 & = & \newline -2 & \times & 0 & = & \newline -2 & \times & -1 & = & \newline -2 & \times & -2 & = & \newline -2 & \times & -3 & = & \newline -2 & \times & -4 & = & \newline \hline \end{array}We know that a negative number multiplied by a positive number gives a negative number as an answer. Use this knowledge to complete the first four rows of the table:
\begin{array}{|r|c|r|c|r|} \hline -2 & \times & +4 & = & -8 \newline -2 & \times & +3 & = & -6 \newline -2 & \times & +2 & = & -4 \newline -2 & \times & +1 & = & -2 \newline -2 & \times & 0 & = & \newline -2 & \times & -1 & = & \newline -2 & \times & -2 & = & \newline -2 & \times & -3 & = & \newline -2 & \times & -4 & = & \newline \hline \end{array}Now, without looking at what is happening in the rows, simply complete the pattern of the numbers in the last column from top to bottom:
\begin{array}{|r|c|r|c|r|} \hline -2 & \times & +4 & = & -8 \newline -2 & \times & +3 & = & -6 \newline -2 & \times & +2 & = & -4 \newline -2 & \times & +1 & = & -2 \newline -2 & \times & 0 & = & 0 \newline -2 & \times & -1 & = & +2 \newline -2 & \times & -2 & = & +4 \newline -2 & \times & -3 & = & +6 \newline -2 & \times & -4 & = & +8 \newline \hline \end{array}The last four rows of the table show that:
Whenever you multiply directed numbers, remember:
Therefore, multiplying:
- the same signs gives
- opposite signs gives .
There are different ways in which we may write multiplication. The following notations all mean the same:
Note that and does NOT mean the same. When you did algebraic expressions last year, you learnt that:
- brackets written next to each other mean multiply:
- plus and minus signs between two numbers separate terms:
Worked example 5.1: Multiplying directed numbers
Carry out the calculation:
-
Step 1: Identify plus and minus signs that separate terms.
-
Step 2: Do multiplication before addition or subtraction. Use the multiplication rules for the signs when you multiply.
Remember the correct order of operations: Brackets, Of, Division, Multiplication, Addition, Subtraction
-
Step 3: Do addition and subtraction last.
Remember, to subtract a negative number is the same as adding the positive of that number.
Exercise 5.1: Multiply directed numbers
Calculate each of the following.
-
-
-
-
-
Remember that when you multiply any number by 1, the number stays the same. But you still need to use the multiplication rules to determine the sign of the answer.
-
\begin{align} &(-2)(-8)(4)(5) \\ =&\;(+16)(4)(5) \\ =&\;(64)(5) \\ =&\;320 \end{align}
-
\begin{align} &(2)(-2)(-4)(4)(-1) \\ =&\;(-4)(-4)(4)(-1) \\ =&\;(+16)(4)(-1) \\ =&\;(64)(-1) \\ =&\;-64 \end{align}
-
\begin{align} &-2\times-2\times5-4\times2 \\ =&\;+4\times5-8 \\ =&\;20-8 \\ =&\;12 \end{align}
-
\begin{align} &-3-8-(2)(-1) \\ =&\;-3-8-(-2) \\ =&\;-3-8+(+2) \\ =&\;-3-6 \\ =&\;-9 \end{align}
-
\begin{align} &2\times-1\times-3+(-2)-(-2)(-4)(-1) \\ =&\;-2\times-3+(-2)-(+8)(-1) \\ =&\;+6+(-2)-(-8) \\ =&\;4+(+8) \\ =&\;12 \end{align}
Dividing directed numbers
From earlier grades you know that we can divide things like money and sweets amongst a certain number of people. For example, if you divide a packet of 48 sweets amongst 3 children, each child gets 16 sweets. We may write this as: or .
You get a positive number when you divide two positive numbers:
We can use bank balances to explain the division of positive and negative numbers. Suppose three friends have a shop. In a certain month, the shop does not do well. It makes a loss and its bank balance shows as \(- ₦15,000\). This means the business owes the bank money. If the debt is shared equally amongst the three friends, each of their bank statements will show \(- ₦5,000\). We may write this as: .
You get a negative number when you divide a negative number by a positive number:
Similarly, suppose the shop does well in another month and its bank balance is \(+ ₦6,000\). The three friends want to withdraw this money in three equal portions, so that they each get \(₦2,000\). Each of the withdrawals will be shown as a negative on the shop's bank statement. We can say there are 3 "negative" transactions that each remove the same amount from the bank account. So we may write this as: .
You get a negative number when you divide a positive number by a negative number:
Suppose the bank charges the shop \(₦750\) bank fees. Somebody at the bank makes a mistake and accidentally puts through the transaction a few times instead of only once. The shop's bookkeeper sees an amount of \(- ₦3,000\) on the bank statement and wants to work out how many times the bank fees were put through. She will do the following calculation: .
You get a positive number when you divide a negative number by a negative number:
Whenever you divide directed numbers, remember:
Therefore, dividing:
- the same signs give
- opposite signs give .
Note that, because the division of two opposite signs always gives a negative answer, it does not matter where we put the minus sign when we write a fraction:
When you give a final answer, you should write the minus sign in front of the whole fraction, as shown in the last step above.
Worked example 5.2: Dividing directed numbers
Calculate:
-
Step 1: Identify plus and minus signs that separate terms.
-
Step 2: First simplify the numerator. Do multiplication before addition or subtraction. Apply the rules for signs when you multiply.
-
Step 3: Now simplify the denominator. Do multiplication before addition or subtraction. Apply the rules for signs when you multiply.
-
Step 4: Simplify the fraction. Apply sign rules when you divide.
Exercise 5.2: Divide directed numbers
Calculate each of the following. Give your answers as mixed numbers where necessary.
-
-
-
-
-
Remember that the number 1 is also a divisive identity. This means when you divide any number by 1, the number stays the same. But you need to apply the rules for signs.
-
\begin{align} &\frac{(-2)(4)(-6)}{(-4)(3)} \\ =&\;\frac{(-8)(-6)}{-12} \\ =&\;\frac{+48}{-12} \\ =&\;-4 \end{align}
-
\begin{align} &\frac{5\times-1+(-15)}{-10\times-4} \\ =&\;\frac{-5+(-15)}{+40} \\ =&\;\frac{-20}{40} \\ =&\;-\frac{1}{2} \end{align}
-
\begin{align} &\frac{(-3)(4)(-2)(2)-(-2)(-3)}{(-1)(-2)(-3)} \\ =&\;\frac{(-12)(-2)(2)-(+6)}{(2)(-3)} \\ =&\;\frac{(24)(2)-(+6)}{-6} \\ =&\;\frac{(48)-(+6)}{-6} \\ =&\;\frac{42}{-6} \\ =&\;-7 \end{align}
-
Remember that zero divided by any number is zero.
\begin{align} &\frac{-3-5(-1)-2}{-1\times-5} \\ =&\;\frac{-3+5-2}{5} \\ =&\;\frac{-5+5}{5} \\ =&\frac{0}{5} \\ =&\;0 \end{align}
-
\begin{align} &\frac{8\times-3\times-1-4(-1)(-2)}{-2-4\times-2} \\ =&\;\frac{-24\times-1-(-4)(-2)}{-2+8} \\ =&\;\frac{+24-(+8)}{6} \\ =&\;\frac{16}{6} \\ =&\;2\frac{4}{6} \\ =&\;2\frac{2}{3} \end{align}
5.2 Squares and square roots
Squares
In Chapter 1 you learnt that a square is the answer we get when we multiply a number by itself. You should revise the section on squares in Chapter 1 before you proceed.
square A square is the answer obtained when any number is multiplied by itself.
From what you have learnt about multiplying directed numbers, you should be able to see that a square is always positive. A negative number cannot be a square, because there is no number that you can multiply by itself to give a negative number as an answer. This is because:
- a positive number multiplied by itself gives a positive answer, for example
- a negative number multiplied by itself also gives a positive answer, for example .
You have also learnt that a perfect square can always be expressed as a product of prime factors that all have a power of two. For example, we know that 144 is a perfect square because we can write it as: . We known that 72 is not a perfect square, because we cannot write it as a product of prime factors that all have the power two. The factors of 72 are .
Worked example 5.3: Determining square numbers
Determine whether is a square. It not, find the smallest number by which it must be multiplied so that the answer is a square.
-
Step 1: Determine whether the number is positive or negative. If it is negative, it is not a square. It must be multiplied by at least .
is negative, so it is not a square.
It must be multiplied by at least : -
Step 2: Express the number from Step 1 as a product of its prime factors.
\begin{array}{r | r} 2 & 162 \newline \hline 3 & 81 \newline \hline 3 & 27 \newline \hline 3 & 9 \newline \hline 3 & 3 \newline \hline & 1 \end{array} -
Step 3: Group the same prime factors in twos and write them in index form.
-
Step 4: Evaluate the powers of the grouped prime factors. If there are any powers NOT equal to 2, the number you obtained in Step 1 is still not a square.
In the prime factors of 162, the power of the 2 is NOT equal to 2. Therefore, 162 is NOT a square.
-
Step 5: Work out by which prime number(s) we must multiply so that all the powers are equal to 2.
In this case, we must multiply by another 2:
The new grouped prime factors are:
The new number is: -
Step 6: Combine the answers from Step 1 and Step 5.
For to be a square, it must be multiplied by and then by :
If is multiplied by , the answer is a square: 324.
Exercise 5.3: Determine square numbers
Determine whether the following numbers or fractions are squares or not. If not, find the smallest number by which each number or fraction must be multiplied to get a square.
-
196
\begin{array}{r | r} 2 & 196 \newline \hline 2 & 98 \newline \hline 7 & 49 \newline \hline 7 & 7 \newline \hline & 1 \end{array}
196 is a square.
-
The numerator is negative, so it is not a square.
The fraction must be multiplied by at least .is a square.
must be multiplied by and simplified to give the square .
-
The number is negative, so it is not a square.
\begin{array}{r | r} 2 & 700 \newline \hline 2 & 350 \newline \hline 5 & 175 \newline \hline 5 & 35 \newline \hline 7 & 7 \newline \hline & 1 \end{array}
It must be multiplied by at least :700 is not a square. It must be multiplied by another 7:
must be multiplied by to give the square 4,900.
Square roots
In Chapter 1 you learnt that a square root is the inverse of a square. The square root of a number is a factor of the number that, when multiplied by itself, gives the number. You should revise the section on square roots in Chapter 1 before you proceed.
square root The factor of a number that, when multiplied by itself, gives the number.
Do not confuse squares and square roots:
- 49 is the square of 7, and we write
- 7 is the square root of 49, and we write .
You have just seen that a negative number cannot be a square. This means that we cannot find the square root of a negative number. There is no factor of a negative number that you can multiply by itself to give that negative number as an answer. For example, does not exist. This is because:
As you can see, this means that a square has two square roots: a positive number and the same negative number. We write it as:
The sign means "plus or minus".
Worked example 5.4: Calculating square roots
Find the square root of .
-
Step 1: Write the fraction as an improper fraction, in the form .
-
Step 2: Write both the numerator and denominator as products of their prime factors.
-
Step 3: Find the square roots of the numerator and denominator separately. Write a sign before the answer.
Square and square root table
The following table shows all the numbers from 1 to 900 that are perfect squares.
\begin{array}{|r|r|r|r|r|r|} \hline 1^2=(-1)^2=1 & \sqrt1=\pm1 & 11^2=(-11)^2=121 & \sqrt{121}=\pm11 & 21^2=(-21)^2=441 & \sqrt{441}=\pm21 \newline 2^2=(-2)^2=4 & \sqrt4=\pm2 & 12^2=(-12)^2=144 & \sqrt{144}=\pm12 & 22^2=(-22)^2=484 & \sqrt{484}=\pm22 \newline 3^2=(-3)^2=9 & \sqrt9=\pm3 & 13^2=(-13)^2=169 & \sqrt{169}=\pm13 & 23^2=(-23)^2=529 & \sqrt{529}=\pm23 \newline 4^2=(-4)^2=16 & \sqrt{16}=\pm4 & 14^2=(-14)^2=196 & \sqrt{196}=\pm14 & 24^2=(-24)^2=576 & \sqrt{576}=\pm24 \newline 5^2=(-5)^2=25 & \sqrt{25}=\pm5 & 15^2=(-15)^2=225 & \sqrt{225}=\pm15 & 25^2=(-25)^2=625 & \sqrt{625}=\pm25 \newline 6^2=(-6)^2=36 & \sqrt{36}=\pm6 & 16^2=(-16)^2=256 & \sqrt{256}=\pm16 & 26^2=(-26)^2=676 & \sqrt{676}=\pm26 \newline 7^2=(-7)^2=49 & \sqrt{49}=\pm7 & 17^2=(-17)^2=289 & \sqrt{289}=\pm17 & 27^2=(-27)^2=729 & \sqrt{729}=\pm27 \newline 8^2=(-8)^2=64 & \sqrt{64}=\pm8 & 18^2=(-18)^2=324 & \sqrt{324}=\pm18 & 28^2=(-28)^2=784 & \sqrt{784}=\pm28 \newline 9^2=(-9)^2=81 & \sqrt{81}=\pm9 & 19^2=(-19)^2=361 & \sqrt{361}=\pm19 & 29^2=(-29)^2=841 & \sqrt{841}=\pm29 \newline 10^2=(-10)^2=100 & \sqrt{100}=\pm10 & 20^2=(-20)^2=400 & \sqrt{400}=\pm20 & 30^2=(-30)^2=900 & \sqrt{900}=\pm30 \newline \hline \end{array}Exercise 5.4: Calculate square roots
Calculate the square roots of the following numbers and fractions. You may use the square and square root table above.
-
From the table:
-
\begin{array}{r | r} 2 & 1,024 \newline \hline 2 & 512 \newline \hline 2 & 256 \newline \hline 2 & 128 \newline \hline 2 & 64 \newline \hline 2 & 32 \newline \hline 2 & 16 \newline \hline 2 & 8 \newline \hline 2 & 4 \newline \hline 2 & 2 \newline \hline & 1 \end{array}
-
From the table:
-
From the table:
-
From the table:
Square and square root notation
Note the following notations when you work with squares and square roots:
- The power of 2 only applies to whatever is directly before it. For example:
, but . - There is a difference between a minus sign that is outside (before) or inside a square root sign. For example:
, but does not exist.
Exercise 5.5: Calculate squares and square roots
Calculate the following. If there is more than one answer, give both.
-
Does not exist.
-
\begin{align} &-\sqrt{16}+(-4)^2 \\ =&\;-(+4)+(+16) \\ =&\;-4+16 \\ =&\; 12 \end{align}
or
\begin{align} &-\sqrt{16}+(-4)^2 \\ =&\;-(-4)+(+16) \\ =&\;+4+16 \\ =&\; 20 \end{align} -
\begin{align} &-3^2-2\times-3 \\ =&\;-9-(-6) \\ =&\;-9+6 \\ =&\; -3 \end{align}
-
\begin{align} &\frac{\sqrt{81}}{(-3)(-3)(3)} \\ =&\;\frac{+9}{(+9)(3)} \\ =&\;\frac{+9}{+27} \\ =&\; \frac{1}{3} \end{align}
or
\begin{align} &\frac{\sqrt{81}}{(-3)(-3)(3)} \\ =&\;\frac{-9}{(+9)(3)} \\ =&\;\frac{-9}{+27} \\ =&\; -\frac{1}{3} \end{align} -
\begin{align} &\frac{\sqrt 4 \times 2 - 2 \times -2}{-2} \\ =&\;\frac{+2\times2-(-4)}{-2} \\ =&\;\frac{4+4}{-2} \\ =&\; \frac{8}{-2} \\ =&\;-4 \end{align}
or
\begin{align} &\frac{\sqrt 4 \times 2 - 2 \times -2}{-2} \\ =&\;\frac{-2\times2-(-4)}{-2} \\ =&\;\frac{-4+4}{-2} \\ =&\; \frac{0}{-2} \\ =&\;0 \end{align}
5.3 Using tables, charts and schedules
Square root table
Apart from the square and square root table you used in the previous section, you can use the following table to determine the square roots of numbers that are not perfect squares. Worked example 5.5 will show you how to do this.
Where applicable, square roots are rounded to two decimal places in this table.
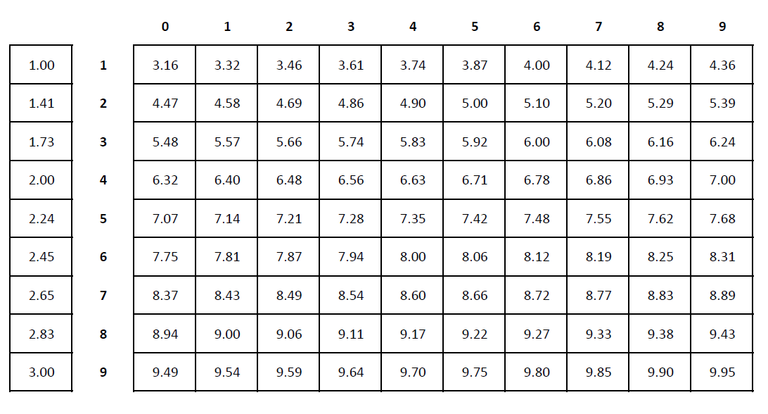
Worked example 5.5: Using a square root table
Find from the square root table.
-
Step 1: Look for the first digit in the vertical column listing the numbers 1 to 9.
The first digit is 7, so you are going to look along the row for the number 7.
-
Step 2: Look for the second digit in the horizontal row listing the numbers 0 to 9.
The second digit is 6, so you are going to look down the column numbered 6.
-
Step 3: The answer is where the row from Step 1 meets the column from Step 2.
-
Step 4: Check whether your answer makes sense.
The two perfect squares on either side of 76 are 64 and 81. This means must lie between and .
The answer 8.72 lies between 8 and 9.
The square roots of the single digits 1 to 9 are shown in the left-most column of the table.
Distance charts
A distance chart can be used to show the distances between different towns. We read a distance chart in a similar way to a square root table. This table shows the shortest distances by road, in kilometres, according to Google Maps, 2019.
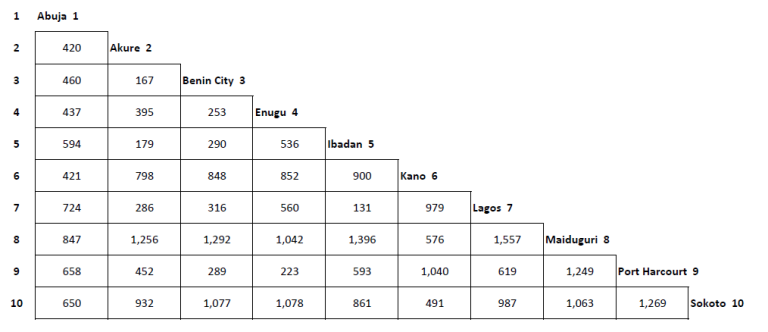
Worked example 5.6: Using a distance chart
Find the distance from Akure to Port Harcourt.
-
Step 1: Look for the names of the two towns. Note the number written next to each town.
Akure is number 2 and Port Harcourt is number 9.
-
Step 2: Go down the column of the town with the lowest number until you reach the row with the same number as the second town.
Go down the column marked Akure 2 until you reach row number 9.
-
Step 3: The answer is where the column and the row from Step 2 intersect. Write it down with the correct units.
The distance is 452 km.
Schedule of costs
The following schedule can be used to work out the cost of any number of articles.
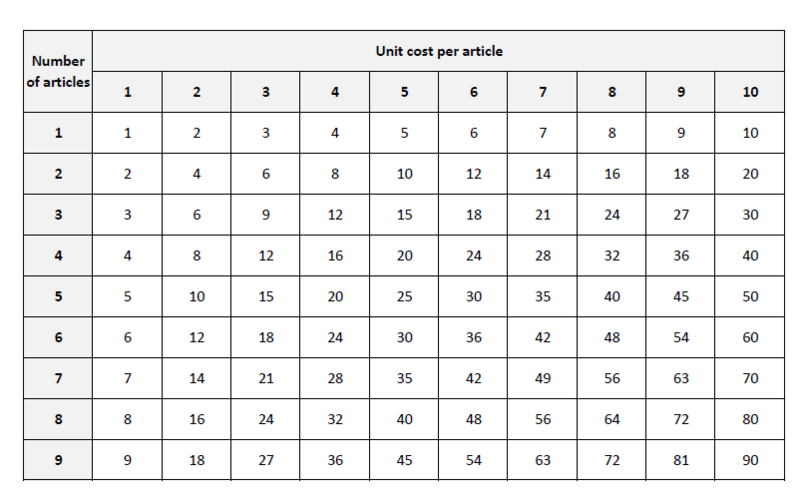
Worked example 5.7: Using a schedule of cost
Use the schedule of cost to determine the cost of 76 cups of beans at \(₦80.50\) per cup.
-
Step 1: Break up the number of items into tens and units. This tells you which rows in the schedule to use.
Use rows 6 and 7.
-
Step 2: Break up the price into hundreds, tens, units and tenths. This tells you which columns in the schedule to use.
\[₦80.50= ₦80+ ₦0.5=( ₦\color{red}8 \color{black} \times 10)+( ₦\color{red}5 \color{black} \div 10)\]Use columns 5 and 8.
-
Step 3: Write the rows and columns you identified in Steps 1 and 2 in a table.
\begin{array}{|c|c|c|} \hline \downarrow \, \rightarrow & 5 & 8 \\ \hline 6 & & \\ \hline 7 & & \\ \hline \end{array} -
Step 4: Insert the multiples of 10 you identified in Steps 1 and 2.
\begin{array}{|c|c|c|} \hline \downarrow \, \rightarrow & 5\, (\div 10) & 8\, (\times 10) \\ \hline 6\, (\times1) & & \\ \hline 7\, (\times 10) & & \\ \hline \end{array} -
Step 5: Refer to the cost schedule. Write down the numbers at the intersections of the rows and columns.
\begin{array}{|c|c|c|} \hline \downarrow \, \rightarrow & 5\, (\div 10) & 8\, (\times 10) \\ \hline 6\, (\times1) & 30 & 48 \\ \hline 7\, (\times 10) & 35 & 56 \\ \hline \end{array} -
Step 6: Determine the total cost by adding the numbers at the intersections of the rows and columns. Apply the multiplications or divisions that you inserted in Step 4.
\begin{align} &(30\times1\div10)+(48\times1\times10)+(35\times10\div10)+(56\times10\times10) \\ =&\;3+480+35+5,600 \\ =&\; ₦6,118 \end{align}
The schedule of cost does not include units, so it can be used for kobos as well.
Exercise 5.6: Use tables, charts and schedules
Use the tables, charts and schedules provided in this chapter to answer the following questions.
- Calculate:
- the side length of a square with an area of 83 cm
From the square root table:
- the area of a square with a side length of 22 cm
From the square and square root table:
- Mustapha wants to tile the floor of a square room. He has 95 tiles. He wants to work out whether there are
enough tiles or whether he must buy more.
- Calculate the maximum number of tiles that he can put along one side of the floor.
From the square root table:
It does not make sense to break the tiles, so the maximum he can put along one side is 9 tiles.- If he tiles the floor according to the previous answer, how many of the 95 tiles will be left over?
He will use tiles.
There will be tiles left over.- The length of one side of the floor is 150 cm. The tiles are square, each with a width of 15 cm. Calculate how many more tiles Mustapha has to buy.
For one length of the floor, he needs tiles.
The room is square, so this means that for the whole floor, he needs tiles.
He must buy another tiles. -
Compare the distance from Benin City to Kano with the distance from Port Harcourt to Abudja.
From the distance chart:
Distance from Benin City to Kano: 848 km
Distance from Port Harcourt to Abudja: 658 kmThe distance from Benin City to Kano is longer than the distance from Port Harcourt to Abudja.
-
Use the schedule of cost to calculate the price of 42 loaves of bread at ₦50 each.
Items:
\begin{align} \text{Cost}&=(20\times10\times10)+(10\times10) \\ &=2,000+100 \\ &= ₦2,100 \end{align}
Cost: ₦50
Numbers at intersections: row 4 and column 5 ; row 2 and column 5 -
A shop owner allows his customers to buy on credit. A brother and sister have the same account and the shop. At the end of a certain month, they owe the shop owner ₦1,250.00. They then decide to split the debit equally. After that, the sister buys 12 litres of vegetable oil at ₦580.00 per litre. They ask the shop owner to send each of them their own account. What will the balance on each account be?
\(\frac{- ₦1,250}{2}=- ₦625\) per person
Litres vegetable oil:
\begin{align} \text{Cost}&=(5\times10\times100)+(8\times10\times10)+(10\times100)+(16\times10) \\ &=5,000+800+1,000+160 \\ &= ₦6,960 \end{align}
Cost: \(₦500+ ₦80\)
Numbers at intersections:Sister's balance: \(-625+(-6,960)=- ₦7,585\)
Brother's balance: \(- ₦625\)
5.4 Summary
- Directed numbers are positive and negative numbers. The sign of a directed number tells us in which direction from zero it lies on the number line.
- Whenever you multiply directed numbers, remember:
- Whenever you divide directed numbers, remember:
- For multiplication and division of directed numbers:
- the same signs give a positive answer
- opposite signs give a negative answer.
- A negative number cannot be a square.
- The square root of a negative number does not exist.
- Square and square root tables, distance charts and cost schedules can be used to determine values without a calculator.
