Chapter 1: Numbers
1.1 Revision of binary numbers
From previous years you know that we use the base ten number system or decimal number system for everyday counting. When we count using the base ten number system, we put objects in groups of ten. We use the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 as digits to make any other number, no matter how big or how small it is.
You also learnt in previous years that the base two number system or binary number system is used in computers and other devices that use computing functions. When we count using the base two number system, we put objects in groups of two. We use only two digits, namely 0 and 1, to make up any number.
base ten number system (decimal number system) The base ten number system or decimal number system is a number system that counts in groups of 10, and uses the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 to represent any number.
base two number system (binary number system) The base two number system or binary number system is a number system that counts in groups of 2, and uses only the digits 0 and 1 to represent any number.
Counting in the base two number system
You have learnt how to count in the base two number system. Remember that we go to a new group each time we reach a number that is a power of 2. We therefore count as follows:
\begin{array}{l l} \circledast & 1 \text{ unit} \\ \color{green}{\circledast \, \circledast} & 1 \text{ group of two and } 0 \text{ units} \\ \color{green}{\circledast \, \circledast} \, \color{black}{\circledast} & 1 \text{ group of two and } 1 \text{ unit} \\ \end{array}If we add another object, we have 2 groups of two, which is 4. We continue counting as follows:
\begin{array}{l l} \color{blue}{\circledast \, \circledast \, \circledast \, \circledast} & 1 \text{ group of four}, \space 0 \text{ groups of two and } 0 \text{ units} \\ \color{blue}{\circledast \, \circledast \, \circledast \, \circledast}\, \color{black}{\circledast} & 1 \text{ group of four}, \space 0 \text{ groups of two and } 1 \text{ unit} \\ \color{blue}{\circledast \, \circledast \, \circledast \, \circledast} \, \color{green}{\circledast \, \circledast} & 1 \text{ group of four}, \space 1 \text{ group of two and } 0 \text{ units} \\ \color{blue}{\circledast \, \circledast \, \circledast \, \circledast} \, \color{green}{\circledast \, \circledast} \, \color{black}{\circledast} & 1 \text{ group of four}, \space 1 \text{ group of two and } 1 \text{ unit} \\ \end{array}If we add another object, we have 3 groups of two, which is 8. We continue counting as follows:
\begin{array}{l l} \color{orange}{\circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast} & 1 \text{ group of eight}, \space 0 \text{ groups of four}, \space 0 \text{ groups of two and } 0 \text{ units} \\ \color{orange}{\circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast} \, \color{black}{\circledast} & 1 \text{ group of eight}, \space 0 \text{ groups of four}, \space 0 \text{ groups of two and } 1 \text{ unit} \\ \color{orange}{\circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast} \, \color{green}{\circledast \, \circledast} & 1 \text{ group of eight}, \space 0 \text{ groups of four}, \space 1 \text{ group of two and } 0 \text{ units} \\ \color{orange}{\circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast} \, \color{green}{\circledast \, \circledast} \, \color{black}{\circledast} & 1 \text{ group of eight}, \space 0 \text{ groups of four}, \space 1 \text{ group of two and } 1 \text{ unit} \\ \color{orange}{\circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast \, \circledast} \, \color{blue}{\circledast \, \circledast \, \circledast \, \circledast} \, & 1 \text{ group of eight}, \space 1 \text{ group of four}, \space 0 \text{ groups of two and } 0 \text{ units} \\ \end{array}We can carry on like this. When we have 4 groups of two, we count in 16s.
Powers of ten and powers of two
In the base ten number system we work with powers of 10. You already know the following powers of 10:
\begin{array}{|l|r|c|} \hline \textbf{Name} & \textbf{Number} & \textbf{Powers of ten} \newline \hline \text{One} & 1 & 10^0 \newline \hline \text{Ten} & 10 & 10^1 \newline \hline \text{Hundred} & 100 & 10^2 \newline \hline \text{Thousand} & 1,000 & 10^3 \newline \hline \text{Ten thousand} & 10,000 & 10^4 \newline \hline \text{Hundred thousand} & 100,000 & 10^5 \newline \hline \text{Million} & 1,000,000 & 10^6 \newline \hline \text{Ten million} & 10,000,000 & 10^7 \newline \hline \text{Hundred million} & 100,000,000 & 10^8 \newline \hline \text{Billion} & 1,000,000,000 & 10^9 \newline \hline \text{Ten billion} & 10,000,000,000 & 10^{10} \newline \hline \text{Hundred billion} & 100,000,000,000 & 10^{11} \newline \hline \text{Trillion} & 1,000,000,000,000 & 10^{12} \newline \hline \end{array}Remember that any number to the power of zero is equal to one. Therefore, .
We can express any number in the base ten number system as the sum of powers of ten.
Worked example 1.1: Writing a decimal number as the sum of powers of 10
Write the number 3,721,568 as the sum of powers of 10.
-
Step 1: Write the number in a place value table.
\begin{array}{|c|c|c|c|c|c|c|} \hline ^\text{millions} & ^\text{hundred thousands} & ^\text{ten thousands} & ^\text{thousands} & ^\text{hundreds} & ^\text{ tens } & ^\text{ units } \newline 1,000,000 & 100,000 & 10,000 & 1,000 & 100 & 10 & 1 \newline (10^6) & (10^5) & (10^4) & (10^3) & (10^2) & (10^1) & (10^0) \newline \hline 3 & 7 & 2 & 1 & 5 & 6 & 8 \newline \hline \end{array} -
Step 2: Write the number as the sum of the values of its digits.
-
Step 3: Write the number as the sum of powers of ten.
\begin{align} \;&3,721,568 \\ &=(3\times10^6)+(7\times10^5)+(2\times10^4)+(1\times10^3)+(5\times10^2)+(6\times10^1)+(8\times10^0) \end{align}
In the base two number system, we work with powers of 2.
The first ten powers of 2 are:
\begin{array}{|l|r|c|} \hline \textbf{Name} & \textbf{Number} & \textbf{Power of 2} \newline \hline \text{One} & 1 & 2^0 \newline \hline \text{Two} & 2 & 2^1 \newline \hline \text{Four} & 4 & 2^2 \newline \hline \text{Eight} & 8 & 2^3 \newline \hline \text{Sixteen} & 16 & 2^4 \newline \hline \text{Thirty two} & 32 & 2^5 \newline \hline \text{Sixty four} & 64 & 2^6 \newline \hline \text{One hundred and twenty eight} & 128 & 2^7 \newline \hline \text{Two hundred and fifty six} & 256 & 2^8 \newline \hline \text{Five hundred and twelve} & 512 & 2^9 \newline \hline \text{One thousand and twenty four} & 1,024 & 2^{10} \newline \hline \end{array}We can also express a decimal number as the sum of powers of 2. This helps us write the decimal number as a binary number.
Worked example 1.2: Writing a decimal number as the sum of powers of 2
\begin{array}{|c|c|c|c|c|c|} \hline \text{thirty twos} & \text{sixteens} & \text{eights} & \text{fours} & \text{twos} & \text{units} \\ (2^5) & (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline & & & & & \\ \hline \end{array}Write the number 53 as the sum of powers of 2. Then write the number in this base two place value table.
-
Step 1: Find the largest power of 2 that is equal to or smaller than 53.
- There is not a power of 2 that is equal to 53.
- , so it is bigger than 53 and we can't use it.
- The next, smaller power of 2 is , and .
- So the largest power of 2 that is equal to or smaller than 53 is .
-
Step 2: Write the given number, 53, as the sum of this power of 2 and what is still left.
So written as a sum, we get:
-
Step 3: Now we have to deal with the 21. Find the largest power of 2 that is equal to or smaller than 21.
-
Step 4: Write the given number, 53, as the sum of all of these numbers.
\begin{align} 53&=32+21 \\ &=32+16+5 \end{align} -
Step 5: Now we have to deal with the 5. Find the largest power of 2 that is equal to or smaller than 5.
-
Step 6: Write the given number, 53, as the sum of all of these numbers.
\begin{align} 53&=32+21 \\ &=32+16+5 \\ &=32+16+4+1 \end{align} -
Step 7: Write the sum of powers of 2 in index form.
Remember that .
-
Step 8: Put the powers of 2 in a base two place value table.
Where you have a power of 2 in your sum, you write a 1 in the place value table.
Where you do not have a power of 2 in your sum, you write a 0 in the place value table. You do not have a or a , so for those place values you write 0.
\begin{array}{|c|c|c|c|c|c|} \hline \text{thirty twos} & \text{sixteens} & \text{eights} & \text{fours} & \text{twos} & \text{units} \\ (2^5) & (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 1 & 0 & 1 & 0 & 1 \\ \hline \end{array} -
Step 9: Write the decimal number as a binary number.
The decimal (base ten) number 53 written as a binary (base two) number is 110101.
We can use this method to write the numbers 1 to 16 in the decimal number system as binary numbers:
\begin{array}{|c|c|c|c|c||c|c|} \hline \text{sixteens} & \text{eights} & \text{fours} & \text{twos} & \text{units} & \text{binary number} & \text{decimal number} \\ (2^4) & (2^3) & (2^2) & (2^1) & (2^0) & & \\ \hline & & & & 1 & 1 & 1 \\ \hline & & & 1 & 0 & 10 & 2 \\ \hline & & & 1 & 1 & 11 & 3 \\ \hline & & 1 & 0 & 0 & 100 & 4 \\ \hline & & 1 & 0 & 1 & 101 & 5 \\ \hline & & 1 & 1 & 0 & 110 & 6 \\ \hline & & 1 & 1 & 1 & 111 & 7 \\ \hline & 1 & 0 & 0 & 0 & 1000 & 8 \\ \hline & 1 & 0 & 0 & 1 & 1001 & 9 \\ \hline & 1 & 0 & 1 & 0 & 1010 & 10 \\ \hline & 1 & 0 & 1 & 1 & 1011 & 11 \\ \hline & 1 & 1 & 0 & 0 & 1100 & 12 \\ \hline & 1 & 1 & 0 & 1 & 1101 & 13 \\ \hline & 1 & 1 & 1 & 0 & 1110 & 14 \\ \hline & 1 & 1 & 1 & 1 & 1111 & 15 \\ \hline 1 & 0 & 0 & 0 & 0 & 10000 & 16 \\ \hline \end{array}Exercise 1.1: Write decimal numbers as the sum of powers of 2
Write each decimal number as the sum of powers of 2. Then write the number in a base two place value table.
Remember the first ten powers of 2:
-
39
\begin{align} 39&=32+7 \\ &=32+4+3 \\ &=32+4+2+1 \\ &=2^5+2^2+2^1+2^0 \end{align} \begin{array}{|c|c|c|c|c|c|c|} \hline (2^6) & (2^5) & (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline & 1 & 0 & 0 & 1 & 1 & 1 \\ \hline \end{array}
-
75
\begin{align} 75&=64+11 \\ &=64+8+3 \\ &=64+8+2+1 \\ &=2^6+2^3+2^1+2^0 \end{align} \begin{array}{|c|c|c|c|c|c|c|} \hline (2^6) & (2^5) & (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 0 & 0 & 1 & 0 & 1 & 1 \\ \hline \end{array}
-
120
\begin{align} 120&=64+56 \\ &=64+32+24 \\ &=64+32+16+8 \\ &=2^6+2^5+2^4+2^3 \end{align} \begin{array}{|c|c|c|c|c|c|c|} \hline (2^6) & (2^5) & (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ \hline \end{array}
-
228
\begin{align} 228&=128+100 \\ &=128+64+36 \\ &=128+64+32+4 \\ &=2^7+2^6+2^5+2^2 \end{align} \begin{array}{|c|c|c|c|c|c|c|c|} \hline (2^7) & (2^6) & (2^5) & (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 \\ \hline \end{array}
-
277
\begin{align} 277&=256+21 \\ &=256+16+5 \\ &=256+16+4+1 \\ &=2^8+2^4+2^2+2^0 \end{align} \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline (2^8) & (2^7) & (2^6) & (2^5) & (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\ \hline \end{array}
Notation of numbers in different number systems
When we work with decimal and binary numbers together, we need a way to identify whether a number is a decimal number or a binary number. For example, the digits 101 represent one hundred and one objects in the base ten number system, but they represent five objects in the base two number system.
We use subscripts to tell us which system a certain combination of digits belong to. For example:
- or means
- or means
We can also work with number systems that have bases other than 10 or 2. In the base 5 number system, for example, we work with powers of five. Here are more examples of what the digits 101 mean in number systems with different bases:
- or means
- or means
- or means
1.2 Converting numbers between different number systems
Converting binary numbers to decimal numbers
Worked example 1.3: Converting binary numbers to decimal numbers
Write as a base ten number.
-
Step 1: Draw up a place value table for the powers of 2. Use the number of digits in the given number to help you do this.
The number has 5 digits. The place value table must have 5 columns.
Start at the right with , and count to the left. So this place value table goes up to .
\begin{array}{|c|c|c|c|c|} \hline \text{sixteens} & \text{eights} & \text{fours} & \text{twos} & \text{units} \\ (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline & & & & \\ \hline \end{array} -
Step 2: Write the given number in the place value table.
\begin{array}{|c|c|c|c|c|} \hline \text{sixteens} & \text{eights} & \text{fours} & \text{twos} & \text{units} \\ (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 1 & 0 & 1 & 0 \\ \hline \end{array} -
Step 3: Write down the place value of each digit. Add all the values to get the base ten number.
\begin{align} & \, 2^4+2^3+0+2^1+0 \\ = & \, 16+8+2 \\ = & \, 26\\ \therefore 11010_\text{two} = & \, 26_\text{ten} \end{align}
Exercise 1.2: Convert binary numbers to base ten numbers
Convert each of the following binary numbers to base ten numbers.
-
\begin{array}{|c|c|c|c|c|} \hline (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline & & 1 & 0 & 1 \\ \hline \end{array} \begin{align} 4 + 1 &= 5 \\ \therefore 101_\text{two}&=5_\text{ten} \end{align}
-
\begin{array}{|c|c|c|c|c|} \hline (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline & 1 & 0 & 0 & 1 \\ \hline \end{array} \begin{align} 8 + 1 &= 9 \\ \therefore 1001_\text{two}&=9_\text{ten} \end{align}
-
\begin{array}{|c|c|c|c|c|} \hline (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 0 & 0 & 1 & 1 \\ \hline \end{array} \begin{align} 16+2+1&=19\\ \therefore 10011_\text{two}&=19_\text{ten} \end{align}
-
\begin{array}{|c|c|c|c|c|} \hline (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 1 & 1 & 1 & 0 \\ \hline \end{array} \begin{align} 16+8+4+2&=30 \\ \therefore 11110_\text{two}&=30_\text{ten} \end{align}
-
\begin{array}{|c|c|c|c|c|c|} \hline (2^5) & (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 1 & 1 & 0 & 1 & 0 \\ \hline \end{array} \begin{align} 32+16+8+2&=58 \\ \therefore 111010_\text{two}&=58_\text{ten} \end{align}
Converting numbers in other bases to decimal numbers
We can use the method shown in the previous worked example to convert numbers in bases other than 2 to decimal numbers.
Whenever you have a number in a given base, you must remember to work with the powers of that base. Here are some examples.
In the base three number system, the first five powers of 3 are:
\begin{array}{|c|r|} \hline \textbf{Power of 3} & \textbf{Number} \newline \hline 3^0 & 1 \newline \hline 3^1 & 3 \newline \hline 3^2 & 9 \newline \hline 3^3 & 27 \newline \hline 3^4 & 81 \newline \hline 3^5 & 243 \newline \hline \end{array}In the base five number system, the first five powers of 5 are:
\begin{array}{|c|r|} \hline \textbf{Power of 5} & \textbf{Number} \newline \hline 5^0 & 1 \newline \hline 5^1 & 5 \newline \hline 5^2 & 25 \newline \hline 5^3 & 125 \newline \hline 5^4 & 625 \newline \hline 5^5 & 3,125 \newline \hline \end{array}In the base 6 number system, the first five powers of 6 are:
\begin{array}{|c|r|} \hline \textbf{Power of 5} & \textbf{Number} \newline \hline 6^0 & 1 \newline \hline 6^1 & 6 \newline \hline 6^2 & 36 \newline \hline 6^3 & 216 \newline \hline 6^4 & 1,296 \newline \hline 6^5 & 7,776 \newline \hline \end{array}Worked example 1.4: Converting numbers in other bases to decimal numbers
Write as a base ten number.
-
Step 1: Draw up a place value table for the powers of the given base. Here we must work with the powers of 5. Note the number of digits in the given number.
The number has 4 digits. The place value table must have 4 columns.
Start at the right with , and count to the left. So this place value table goes up to .
\begin{array}{|c|c|c|c|} \hline (5^3) & (5^2) & (5^1) & (5^0) \\ \hline & & & \\ \hline \end{array} -
Step 2: Write the given number in the place value table.
\begin{array}{|c|c|c|c|} \hline (5^3) & (5^2) & (5^1) & (5^0) \\ \hline 2 & 4 & 3 & 2 \\ \hline \end{array} -
Step 3: Write down the place value of each digit. Add all the values to get the base ten number.
Except for the base 2 number system, we may have more than one group of a specific power. Look at the place value table in Worked example 1.1 again.
\begin{align} & \, (2\times5^3)+(4\times 5^2)+(3\times 5^1)+(2\times5^0) \\ = & \, (2\times125)+(4\times 25)+(3\times 5)+(2\times1) \\ = & \, 250+100+15+2 \\ = & \, 367 \\ \therefore 2,432_\text{five} = & \,367_\text{ten} \end{align}
Exercise 1.3: Convert numbers in other bases to base ten numbers
Convert each of the following numbers to base ten numbers.
-
\begin{array}{|c|c|c|c|} \hline (3^3) & (3^2) & (3^1) & (3^0) \\ \hline 1 & 2 & 0 & 1 \\ \hline \end{array} \begin{align} 1,201_\text{three} &= (1\times3^3) + (2\times 3^2) + (0\times 3^1) + (1 \times 3^0) \\ &= (1\times27) + (2\times 9) + (0\times 3) + (1 \times 1) \\ &= 27+18+0+1\\ &=46_\text{ten} \end{align}
-
\begin{array}{|c|c|c|} \hline (6^2) & (6^1) & (6^0) \\ \hline 1 & 4 & 5 \\ \hline \end{array} \begin{align} 145_\text{six} &= (1\times 6^2) + (4\times 6^1) + (5 \times 6^0) \\ &= (1\times36) + (4\times 6) + (5\times 1) \\ &= 36+24+5\\ &=65_\text{ten} \end{align}
-
\begin{array}{|c|c|c|c|} \hline (9^3) & (9^2) & (9^1) & (9^0) \\ \hline 5 & 0 & 8 & 4 \\ \hline \end{array} \begin{align} 5,084_\text{nine} &= (5\times9^3) + (0\times 9^2) + (8\times 9^1) + (4 \times 9^0) \\ &= (5\times729) + (0\times 81) + (8\times 9) + (4 \times 1) \\ &= 3,645+0+72+4\\ &=3,721_\text{ten} \end{align}
-
\begin{array}{|c|c|c|} \hline (11^2) & (11^1) & (11^0) \\ \hline 1 & 2 & 8 \\ \hline \end{array} \begin{align} 128_\text{eleven} &= (1\times 11^2) + (2\times 11^1) + (8 \times 11^0) \\ &= (1\times 121) + (2\times 11) + (8\times 1) \\ &= 121+22+8\\ &=151_\text{ten} \end{align}
-
\begin{array}{|c|c|c|c|c|} \hline (7^4) & (7^3) & (7^2) & (7^1) & (7^0) \\ \hline 2 & 0 & 0 & 3 & 5 \\ \hline \end{array} \begin{align} 20,035_\text{seven} &= (2\times 7^4) + (0\times7^3) + (0\times 7^2) + (3\times 7^1) + (5 \times 7^0) \\ &= (2\times2,401) + (0\times 343) + (0\times 49) + (3 \times 7) + (5 \times 1) \\ &= 4,802+0+0+21+5\\ &=4,828_\text{ten} \end{align}
Converting decimal numbers to binary numbers
Worked example 1.5: Converting decimal numbers to binary numbers
Write as a base two number.
-
Step 1: Divide the given number repeatedly by 2, until you get zero. For each division, write down whether the remainder is 0 or 1.
\begin{array}{r|rr} 2 & 23 & \\ \hline 2 & 11 & \text{remainder: }1 \\ \hline 2 & 5 & \text{remainder: }1 \\ \hline 2 & 2 & \text{remainder: }1 \\ \hline 2 & 1 & \text{remainder: }0 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array} -
Step 2: Write down the remainders from bottom to top. This gives the corresponding binary number.
If you do not feel comfortable with the method explained here, you can write the decimal number as the sum of powers of 2 and then use a place value table. This is shown in Worked example 1.2.
Exercise 1.4: Convert decimal numbers to base two numbers
Convert each of the following decimal numbers to base two numbers.
Remember that when you write down the remainders to get the binary number, you start from the bottom remainder and go up to the top one.
-
\begin{array}{r|rr} 2 & 7 & \\ \hline 2 & 3 & \text{remainder: }1 \\ \hline 2 & 1 & \text{remainder: }1 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array}
-
\begin{array}{r|rr} 2 & 11 & \\ \hline 2 & 5 & \text{remainder: }1 \\ \hline 2 & 2 & \text{remainder: }1 \\ \hline 2 & 1 & \text{remainder: }0 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array}
-
\begin{array}{r|rr} 2 & 29 & \\ \hline 2 & 14 & \text{remainder: }1 \\ \hline 2 & 7 & \text{remainder: }0 \\ \hline 2 & 3 & \text{remainder: }1 \\ \hline 2 & 1 & \text{remainder: }1 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array}
-
\begin{array}{r|rr} 2 & 36 & \\ \hline 2 & 18 & \text{remainder: }0 \\ \hline 2 & 9 & \text{remainder: }0 \\ \hline 2 & 4 & \text{remainder: }1 \\ \hline 2 & 2 & \text{remainder: }0 \\ \hline 2 & 1 & \text{remainder: }0 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array}
-
\begin{array}{r|rr} 2 & 65 & \\ \hline 2 & 32 & \text{remainder: }1 \\ \hline 2 & 16 & \text{remainder: }0 \\ \hline 2 & 8 & \text{remainder: }0 \\ \hline 2 & 4 & \text{remainder: }0 \\ \hline 2 & 2 & \text{remainder: }0 \\ \hline 2 & 1 & \text{remainder: }0 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array}
Converting decimal numbers to numbers in other bases
We can use the method shown in the previous worked example to convert decimal numbers to numbers in bases other than 2.
Worked example 1.6: Converting decimal numbers to numbers in other bases
Write as a base six number.
-
Step 1: Divide the given number repeatedly by the given base, until you get zero. For each division, write down the remainder.
The given base is 6.
\begin{array}{r|rr} 6 & 1,352 & \\ \hline 6 & 225 & \text{remainder: }2 \\ \hline 6 & 37 & \text{remainder: }3 \\ \hline 6 & 6 & \text{remainder: }1 \\ \hline 6 & 1 & \text{remainder: }0 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array} -
Step 2: Write down the remainders from bottom to top. This gives the corresponding base six number.
If you do not feel comfortable with the method explained here, you can write the decimal number as the sum of powers of 6:
\begin{align} 1,352&=1,296+56 \\ &= 1,296+36+20 \\ &=1,296+36+6+6+6+2 \\ &= 6^4+6^2+6^1+6^1+6^1+2 \end{align} \begin{array}{|c|c|c|c|c|} \hline (6^4) & (6^3) & (6^2) & (6^1) & (6^0) \\ \hline 1 & 0 & 1 & 3 & 2 \\ \hline \end{array}
Exercise 1.5: Convert decimal numbers to numbers in other bases
Convert each of the following decimal numbers to numbers in the given bases.
Remember that when you write down the remainders, you start from the bottom one and go up to the top one.
-
Convert to a base 3 number.
\begin{array}{r|rr} 3 & 11 & \\ \hline 3 & 3 & \text{remainder: }2 \\ \hline 3 & 1 & \text{remainder: }0 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array}
-
Convert to a base 7 number.
\begin{array}{r|rr} 7 & 25 & \\ \hline 7 & 3 & \text{remainder: }4 \\ \hline & 0 & \text{remainder: }3 \\ \hline \end{array}
-
Convert to a base 4 number.
\begin{array}{r|rr} 4 & 121 & \\ \hline 4 & 30 & \text{remainder: }1 \\ \hline 4 & 7 & \text{remainder: }2 \\ \hline 4 & 1 & \text{remainder: }3 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array}
-
Convert to a base 5 number.
\begin{array}{r|rr} 5 & 326 & \\ \hline 5 & 65 & \text{remainder: }1 \\ \hline 5 & 13 & \text{remainder: }0 \\ \hline 5 & 2 & \text{remainder: }3 \\ \hline & 0 & \text{remainder: }2 \\ \hline \end{array}
-
Convert to a base 12 number.
\begin{array}{r|rr} 12 & 2,065 & \\ \hline 12 & 172 & \text{remainder: }1 \\ \hline 12 & 14 & \text{remainder: }4 \\ \hline 12 & 1 & \text{remainder: }2 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array}
Convert between number systems that have bases other than ten
Worked example 1.7: Converting between number systems that have bases other than ten
Write as a base two number.
-
Step 1: Convert the given number to a decimal number. Start with a place value table that has the powers of the given base.
- The given base is 4, so we must work with the powers of 4.
- The number has 3 digits, so the place value table must have 3 columns.
-
Step 2: Write down the place value of each digit. Add all the values to get the decimal number.
Remember that we may have more than one group of a specific power.
\begin{align} & \, (1\times 4^2)+(1\times 4^1)+(3\times4^0) \\ = & \, (1\times 16)+(1\times 4)+(3\times1) \\ = & \, 16+4+3 \\ = & \, 23 \\ \therefore 113_\text{four} = & \, 23_\text{ten} \end{align} -
Step 3: Convert the decimal number from Step 2 to a number with the required base. Start by dividing the decimal number repeatedly by the required base, until you get zero. Write down the remainders.
The required base is 2.
\begin{array}{r|rr} 2 & 23 & \\ \hline 2 & 11 & \text{remainder: }1 \\ \hline 2 & 5 & \text{remainder: }1 \\ \hline 2 & 2 & \text{remainder: }1 \\ \hline 2 & 1 & \text{remainder: }0 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array} -
Step 4: Write down the remainders from bottom to top. This gives the corresponding base two number.
-
Step 5: Write down the answer.
Exercise 1.6: Convert between number systems that have bases other than ten
Convert each of the following numbers.
-
Convert to a base 4 number.
\begin{array}{|c|c|c|c|} \hline (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 0 & 1 & 1 \\ \hline \end{array} \begin{align} 1011_2&=2^3+0+2^1+2^0\\ &= 8+2+1\\ &=11_{10} \end{align} \begin{array}{r|rr} 4 & 11 & \\ \hline 4 & 2 & \text{remainder: }3 \\ \hline & 0 & \text{remainder: }2 \\ \hline \end{array} \begin{align} 11_{10}& =23_4 \\ \therefore 1011_\text{two}& =23_\text{four} \end{align}
-
Convert to a base 2 number.
\begin{array}{|c|c|} \hline (8^1) & (8^0) \\ \hline 6 & 2 \\ \hline \end{array} \begin{align} 62_8&=(6\times8^1)+(2\times8^0)\\ &= 48+2\\ &=50_{10} \end{align} \begin{array}{r|rr} 2 & 50 & \\ \hline 2 & 25 & \text{remainder: }0\\ \hline 2 & 12 & \text{remainder: }1\\ \hline 2 & 6 & \text{remainder: }0 \\ \hline 2 & 3 & \text{remainder: }0 \\ \hline 2 & 1 & \text{remainder: }1 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array} \begin{align} 50_{10}& =110010_2 \\ \therefore 62_\text{eight}& =110010_\text{two} \end{align}
-
Convert to a base 5 number.
\begin{array}{|c|c|c|c|c|} \hline (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 0 & 0 & 1 & 1 \\ \hline \end{array} \begin{align} 10011_2&=2^4+0+0+2^1+2^0\\ &= 16+2+1\\ &=19_{10} \end{align} \begin{array}{r|rr} 5 & 19 & \\ \hline 5 & 3 & \text{remainder: }4 \\ \hline & 0 & \text{remainder: }3 \\ \hline \end{array} \begin{align} 19_{10}&=34_5 \\ \therefore 10011_\text{two}&=34_\text{five} \end{align}
-
Convert to a base 2 number.
\begin{array}{|c|c|} \hline (6^2) & (6^1) & (6^0) \\ \hline 3 & 0 & 4 \\ \hline \end{array} \begin{align} 304_6&=(3\times6^2)+0+(4\times6^0)\\ &= (3\times 36)+(4\times 1)\\ &=112_{10} \end{align} \begin{array}{r|rr} 2 & 112 & \\ \hline 2 & 56 & \text{remainder: }0\\ \hline 2 & 28 & \text{remainder: }0\\ \hline 2 & 14 & \text{remainder: }0 \\ \hline 2 & 7 & \text{remainder: }0 \\ \hline 2 & 3 & \text{remainder: }1 \\ \hline 2 & 1 & \text{remainder: }1 \\ \hline & 0 & \text{remainder: }1 \\ \hline \end{array}
\begin{align} 112_{10}&=1110000_2 \\ \therefore 304_\text{six}&=1110000_\text{two} \end{align}
-
Convert to a base 7 number.
\begin{array}{|c|c|c|c|c|} \hline (2^4) & (2^3) & (2^2) & (2^1) & (2^0) \\ \hline 1 & 1 & 1 & 0 & 1 \\ \hline \end{array} \begin{align} 11101_2&=2^4+2^3+2^2+0+2^0\\ &= 16+8+4+1\\ &=29_{10} \end{align} \begin{array}{r|rr} 7 & 29 & \\ \hline 7 & 4 & \text{remainder: }1 \\ \hline & 0 & \text{remainder: }4 \\ \hline \end{array} \begin{align} 29_{10}&=41_7 \\ \therefore 11101_\text{two}&=41_\text{seven} \end{align}
1.3 Interpretation of word problems
In previous years you used algebraic expressions and equations to solve word problems. Here are some tips that you should already know:
- The sum of two numbers means they must be added, for example the sum of 15 and 20 is .
- The difference between two numbers means they must be subtracted, for example the difference between 20 and 15 is . Unless otherwise stated, subtract the smaller number from the larger number.
- The product of two numbers means they must be multiplied, for example the product of 5 and 3 is .
- Three consecutive numbers can be represented as .
- More than means we must add, for example 5 more than is .
- Less than means we must subtract, for example 5 less than is .
- Double or twice means we must multiply by 2, for example double or twice is .
- Half means we must divide by 2, for example half of is or .
- Seconds in minutes and hours are and .
- Kobo in naira is .
- The area of a square is given by . The perimeter of a square is given by .
- The area of a rectangle is given by . The perimeter of a rectangle is given by .
Exercise 1.7: Practise interpreting word problems
-
Find the sum of , , and .
\begin{align} &6x+(-2x)+6y+y \\ &=4x+7y \end{align}
-
Double the difference between and .
\begin{align} &(16a-12a)\times 2 \\ &=4a\times2 \\ &=8a \end{align}
-
A daughter is currently half the age of her father. If her father's current age is years, how old will the daughter be in 10 years' time?
The father is currently years old.
The daughter is therefore years old.
In ten years' time the daughter will be years.
-
A long-distance athlete covers an average distance of per minute. How far does she run in ?
Minutes in hours:
She runs:
-
The sum of three consecutive numbers is . If the first of the three numbers is , determine .
The numbers are , and .
\begin{align} y&=a+(a+1)+(a+2) \\ &=a+a+1+a+2 \\ &=a+a+a+1+2 \\ &=3a+3 \end{align} -
A shop owner sells rice at \(₦\,x\) per cup. She also sells maize per cup, at half the price of the rice. If she sold 50 cups of rice and 30 cups of maize, what was her income?
The price of her rice is per cup.
The price of her maize is therefore per cup.
Her income is:
\begin{align} &(50\times x)+(30\times \frac{1}{2}x) \\ &=50x+15x \\ &=65x \end{align} -
The length of a rectangle is 3 cm more than its breadth. Calculate the perimeter of the rectangle.
\begin{align} P&=2l+2b \\ &=2(b+3)+2b \\ &=2b+6+2b \\ &=4b+6 \text{ cm} \end{align}
-
The product of three numbers is 180. If two of the numbers are 15 and 3, find the third number.
Let the number be .
\begin{align} 15\times3\times x &= 180 \\ 45x&=180 \\ \frac{45x}{45}&=\frac{180}{45} \\ x&=4 \end{align} -
The product of 5 and two more than a certain number is 20. Find the number.
Let the number be .
\begin{align} 5\times(x+2) &= 20 \\ 5(x+2) &= 20 \\ 5x+10&=20 \\ 5x+10-10&=20-10 \\ 5x&=10 \\ \frac{5x}{5}&=\frac{10}{5} \\ x&=2 \end{align} -
The side length of square P is units. The side length of square Q is 4 units longer than that of square P. Calculate the area of each square.
Square P:
Square Q:
\begin{align} A&=(x+4)^2\\ &=(x+4)(x+4)\\ &=x^2+8x+16 \text{ square units} \end{align}
1.4 Simplifying algebraic expressions
From previous years you know that an algebraic expression is a mathematical phrase or statement that contains numbers, symbols, variables (such as or ) and operators (such as , , and ). Algebraic expressions do not have equals signs.
algebraic expression An algebraic expression is a mathematical statement that contains a combination of numbers, symbols, variables and mathematical operators. It does not have an equals sign.
Simplifying algebraic expressions with brackets
We expand an algebraic expression when we use the distributive law to remove brackets and then collect like terms. Here are some examples of how this law can be applied:
expand We expand an algebraic expression by using the distributive law to remove brackets and then collecting like terms.
distributive law The distributive law states that the multiplying factor or coefficient of a bracket can be distributed across each of the terms inside the bracket, for example .
Remember that the correct order of operations is:
- Brackets
- Of
- Division
- Multiplication
- Addition
- Subtraction
Worked example 1.8: Expanding algebraic expressions
Expand and simplify:
-
Step 1: Start with the brackets. Multiply the two terms that stand first in each bracket.
Remember, when you multiply or divide positive and negative numbers:
- The same signs give a positive answer.
- Opposite signs give a negative answer.
-
Step 2: Multiply the two terms that stand on the outsides, that is, the furthest away from each other.
-
Step 3: Multiply the two terms that stand on the insides, that is, the closest together.
-
Step 4: Multiply the two terms that stand last in each bracket.
-
Step 5: Combine the answers from Steps 1 to 4. All three terms must be multiplied by .
The acronym FOIL may help you remember the above method:
First term in each bracket
Outside terms
Inside terms
Last term in each bracket -
Step 6: Collect like terms.
-
Step 7: Apply the distributive law again.
Exercise 1.8: Expand algebraic expressions
Expand and simplify the following algebraic expressions.
-
\begin{align} &\,(4b-2c)(2b-4c) \\ = &\,8b^2-16bc-4bc+8c^2 \\ = &\,8b^2-20bc+8c^2 \\ \end{align}
-
\begin{align} &\,2(x+y)-3(x-y) \\ =&\,2 \times x +2 \times y -3 \times x -3 \times -y \\ =&\,2x+2y-3x+3y \\ =&\,-x+5y \end{align}
-
\begin{align} &\,5(2b-c)(2b+c) \\ =&\,5(4b^2-c^2) \\ =&\,20b^2-5c^2 \\ \end{align}
-
\begin{align} &\,2+(2m-3)(6m-4) \\ =&\,2+12m^2-8m-18m+12 \\ =&\,12m^2-26m+14 \\ \end{align}
-
\begin{align} &\,(p+q)^2-2(p+q)^2 \\ =&\,p^2+p \times q \times 2 +q^2 -2(p^2+p \times q \times 2+q^2) \\ =&\,p^2+2pq+q^2-2(p^2+2pq+q^2) \\ =&\,p^2+2pq+q^2-2p^2-4pq-2q^2 \\ =&\,-p^2-2pq-q^2 \end{align}
Simplifying algebraic expressions with fractions
Worked example 1.9: Multiplying and dividing fractions
Simplify:
-
Step 1: Do the division first.
- Find the HCF of the coefficients and simplify them. The HCF of 4 and 10 is 2.
- Write out the variables and simplify them.
- Decide what the sign of the answer must be.
-
Step 2: Use the answer from Step 1 to do the multiplication.
- Multiply the coefficients.
- Multiply the variables.
- Decide what the sign of the answer must be.
-
Step 3: Repeat Step 1 if needed.
Worked example 1.10: Adding and subtracting fractions
Simplify:
-
Step 1: Find the LCD of the denominators.
- The LCD of 2 and 4 is 4.
- The LCD of and is .
-
Step 2: Find equivalent fractions with the LCD from Step 1 as their denominator.
Remember, to find an equivalent fraction, you multiply or divide both the numerator and the denominator by the same numbers or variables.
\begin{align} &\frac{5}{4x}-\frac{1+x}{x^2}+\frac{4}{2x} \\ =&\frac{5\;{\color{red}{(\times x)}}}{4x\;{\color{red}{(\times x)}}}-\frac{1+x\;{\color{red}{(\times4)}}}{x^2\;{\color{red}{(\times 4)}}}+\frac{4\;{\color{red}{(\times 2x)}}}{2x\;{\color{red}{(\times 2x)}}} \\ =&\frac{5x-4(1+x)+4(2x)}{4x^2} \\ \end{align}Remember, when fractions have the same denominator, we simply add or subtract the numerators.
-
Step 5: If needed, expand the numerators.
\begin{align} &\frac{5}{4x}-\frac{1+x}{x^2}+\frac{4}{2x} \\ =&\frac{5x-4(1+x)+4(2x)}{4x^2} \\ =&\frac{5x-4-4x+8x}{4x^2} \end{align} -
Step 6: Collect like terms and simplify.
\begin{align} & \frac{5}{4x}-\frac{1+x}{x^2}+\frac{4}{2x} \\ =&\frac{5x-4(1+x)+4(2x)}{4x^2} \\ =&\frac{5x-4-4x+8x}{4x^2}\\ =&\frac{9x-4}{4x^2} \end{align}
Exercise 1.9: Simplify algebraic expressions with fractions
Simplify the following algebraic expressions.
-
\begin{align} &\frac{1}{3x}-\frac{2}{3y} \\ &= \frac{y(1)-x(2)}{3xy} \\ &= \frac{y-2x}{3xy} \\ \end{align}
-
\begin{align} &\frac{2b+3a}{6}-\frac{4a}{5} \\ &=\frac{5(2b+3a)-6(4a)}{30} \\ &=\frac{10b+15a-24a}{30} \\ &=\frac{10b-9a}{30} \end{align}
-
\begin{align} &-\frac{3x^3}{4xy} \times \frac{8y^2}{9x} \\ &=-\frac{3\times x \times x \times x \times 8 \times y \times y}{4 \times x \times y \times 9 \times x} \\ &=-\frac{\cancel 3^1 \times \cancel x \times \cancel x \times x \times \cancel 8^2 \times \cancel y \times y}{\cancel 4^1 \times \cancel x \times \cancel y \times \cancel 9^3 \times \cancel x} \\ &=-\frac{2xy}{3} \end{align}
-
\begin{align} &\frac{m+2}{ab}+\frac{3}{a^2} \\ &=\frac{a(m+2)+b(3)}{a^2 b} \\ &=\frac{am+2a+3b}{a^2b} \\ \end{align}
-
\begin{align} &\frac{x^3}{5}\times\frac{10}{x^2}+\frac{3}{x}\times\frac{x}{6x} \\ &=\frac{x \times x \times x \times 10}{5\times x \times x}+\frac{3\times x}{x\times6 \times x} \\ &=\frac{\cancel x \times \cancel x \times x \times \cancel{10}^2}{\cancel 5^1 \times \cancel x \times \cancel x}+\frac{\cancel 3^1 \times \cancel x}{\cancel x\times \cancel 6^2 \times x} \\ &=\frac{2x}{1}+\frac{1}{2x} \\ &=\frac{2x \;(\times 2x)}{1\;(\times 2x)}+\frac{1}{2x} \\ &=\frac{4x^2}{2x}+\frac{1}{2x}\\ &=\frac{4x^2+1}{2x} \end{align}
Simplifying algebraic expressions with brackets and fractions
Sometimes it is necessary to factorise part of an algebraic expression before we can simplify it. Factorising an algebraic expression is the reverse of expanding it. We can represent the two processes as follows:
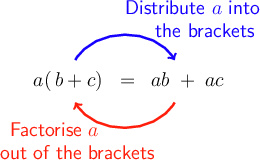
factorise We factorise an algebraic expression by writing it as a product of factors that can be multiplied to give the original expression.
Worked example 1.11: Simplifying algebraic expressions with brackets and fractions
Simplify:
-
Step 1: If the numerator or denominator of a term already has brackets, factorise the rest of the term as well.
\begin{align} &\frac{(x+2)(x-4)}{x^2+2x}+\frac{2}{3x}\\ =&\frac{(x+2)(x-4)}{x(x+2)}+\frac{2}{3x}\\ \end{align} -
Step 2: Simplify each term before you add or subtract.
\begin{align} &\frac{(x+2)(x-4)}{x^2+2x}+\frac{2}{3x}\\ =&\frac{\cancel{(x+2)}(x-4)}{x\cancel{(x+2)}}+\frac{2}{3x}\\ =&\frac{x-4}{x}+\frac{2}{3x}\\ \end{align}Treat a bracket as you would treat a single variable. Just as , so .
-
Step 3: Find the LCD, create equivalent equations, and then add and subtract terms and simplify.
\begin{align} &\frac{x-4}{x}+\frac{2}{3x}\\ =&\frac{3(x-4)}{3x}+\frac{2}{3x}\\ =&\frac{3x-12+2}{3x} \\ =&\frac{3x-10}{3x} \end{align}
Exercise 1.10: Simplify algebraic expressions with brackets and fractions
Simplify the following algebraic expressions.
-
\begin{align} &\frac{(x-3)(x-1)}{x^2-x} \\ &=\frac{(x-3)(x-1)}{x(x-1)} \\ &=\frac{(x-3)\cancel{(x-1)}}{x\cancel{(x-1)}}\\ &=\frac{x-3}{x} \end{align}
-
If you cannot simplify anything, factorise the numerator and denominator.
\begin{align} &\frac{a^2b+ab^2}{a^2+ab} \\ &=\frac{ab(a+b)}{a(a+b)} \\ &=\frac{ab\cancel{(a+b)}}{a\cancel{(a+b)}}\\ &=\frac{\cancel a b}{\cancel a}\\ &=b \end{align}
-
Simplify the first term before you add.
\begin{align} &\frac{x^2+2x}{2x^3+4x^2}+\frac{5}{x} \\ &=\frac{x(x+2)}{2x^2(x+2)}+\frac{5}{x} \\ &=\frac{\cancel x\cancel{(x+2)}}{2\times x \times \cancel x \cancel{(x+2)}}+\frac{5}{x}\\ &=\frac{1}{2x}+\frac{5}{x}\\ &=\frac{1}{2x}+\frac{5\;(\times2)}{x\;(\times 2)}\\ &=\frac{1+10}{2x} \\ &=\frac{11}{2x} \end{align}
-
Just as the LCD of and is , the LCD of and is .
\begin{align} &\frac{y+2}{y-2}-\frac{y+3}{y-3} \\ &=\frac{y+2\phantom{0}\times(y-3)}{y-2\phantom{0}\times(y-3)}-\frac{y+3\phantom{0}\times(y-2)}{y-3\phantom{0}\times(y-2)} \\ &=\frac{(y+2)(y-3)-(y+3)(y-2)}{(y-2)(y-3)}\\ &=\frac{y^2-y-6-(y^2+y-6)}{y^2-5y+6}\\ &=\frac{y^2-y-6-y^2-y+6}{y^2-5y+6}\\ &=\frac{y^2-y^2-y-y-6+6}{y^2-5y+6}\\ &=\frac{-2y}{y^2-5y+6}\text{ OR } \frac{-2y}{(y-2)(y-3)} \\ \end{align}
Remember, when we add or subtract fractions with the same denominator, we add or subtract the numerators and write the answer over the common denominator.
-
\begin{align} &\frac{1}{a+1}-\frac{a+1}{4}+\frac{a^2-5}{4(a+1)} \\ &=\frac{1\phantom{0}\times(4)}{a+1\phantom{0}\times(4)}-\frac{a+1\phantom{0}\times(a+1)}{4\phantom{0}\times(a+1)}+\frac{a^2-5}{4(a+1)} \\ &=\frac{4-(a+1)(a+1)+a^2-5}{4(a+1)}\\ &=\frac{4-(a^2+2a+1)+a^2-5}{4(a+1)}\\ &=\frac{4-a^2-2a-1+a^2-5}{4(a+1)}\\ &=\frac{-a^2+a^2-2a-5-1+4}{4(a+1)}\\ &=\frac{-2a-2}{4(a+1)}\\ &=\frac{-2(a+1)}{4(a+1)}\\ &=\frac{-\cancel 2^1\cancel{(a+1)}}{\cancel 4^2\cancel{(a+1)}}\\ &=-\frac{1}{2} \end{align}
1.5 Direct and inverse proportion
Direct proportion
A direct proportion is a relationship between two variable quantities of which the ratio is constant. The one quantity is a constant multiple of the other. We say the quantities are directly proportional to each other. This means if one quantity increases, the other increases in the same ratio. Similarly, if one quantity decreases, the other decreases in the same ratio.
If is directly proportional to , we write in symbols:
Because the two variables have a constant ratio, we can write:
The value of remains constant and is therefore called the proportionality constant.
We can rearrange the equation as follows:
This shows that is a constant multiple of .
direction proportion A direct proportion is a relationship between two variable quantities of which the ratio is constant because the one quantity is a constant multiple of the other.
directly proportional Two variable quantities are directly proportional if their ratio is constant because the one quantity is a constant multiple of the other.
proportionality constant In a direct proportion, the proportionality constant is the constant ratio of one variable quantity to another.
Worked example 1.12: Applying a direct proportion
The following table of values represents the movement of a cyclist.
\begin{array}{|l|c|c|c|c|c|} \hline \text{Time passed in hours } (t) & 1 & 2 & 3 & 4 & 5 \\ \hline \text{Distance travelled in kilometres }(D) & 20 & 40 & 60 & 80 & 100 \\ \hline \end{array}
- Prove that the distance the cyclist travelled is directly proportional to the time that passed.
- What does the proportionality constant represent?
- Write an equation for the relationship between distance and time.
- Draw a graph of distance versus time.
-
Step 1: If the two variables are directly proportional, their ratio must be constant.
From the table of values:
\begin{align} \frac{D}{t}&=\frac{20}{1}=20 \\ \frac{D}{t}&=\frac{40}{2}=20 \\ \frac{D}{t}&=\frac{60}{3}=20 \\ \frac{D}{t}&=\frac{80}{4}=20 \\ \frac{D}{t}&=\frac{100}{5}=20 \end{align}The ratio is constant, therefore .
-
Step 2: The proportionality constant is the constant ratio of the two variables.
In this case, the proportionality constant represents the speed of the cyclist, which is 20Â km/h.
-
Step 3: Distance must be a constant multiple of time.
The equation is:
-
Step 4: Plot the graph from the table of values.
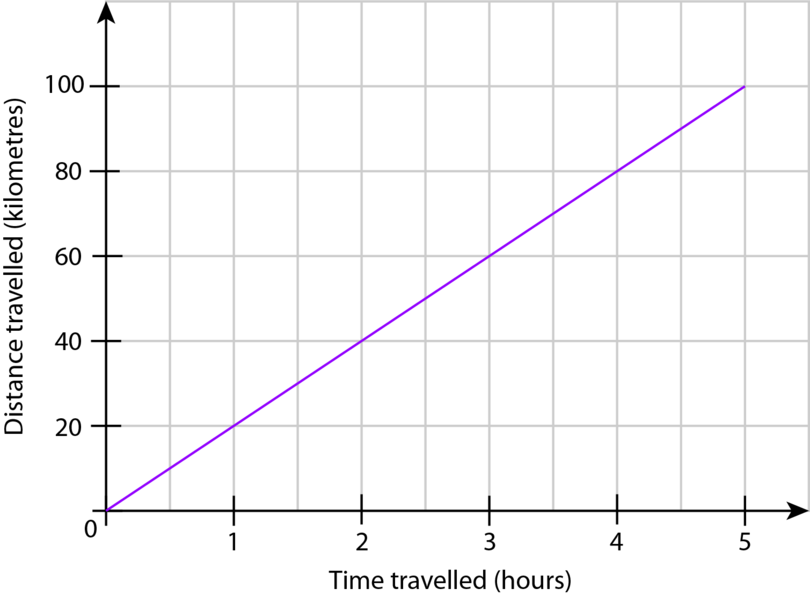
The graph is a straight line through the origin.
Exercise 1.11: Apply direct proportion
-
The volume of fuel used by a truck is directly proportional to the distance the truck travels. The truck can travel 400Â km on 50Â litres of fuel.
- Calculate the proportionality constant for the relationship between volume of fuel and distance.
\begin{align} \frac{\text{volume of fuel}}{\text{distance}} &= \frac{50}{400} \\ &=\frac{1}{8} \end{align}
- What does the proportionality constant represent?
It represents the fuel consumption of the truck, which is  L/km or 0.125 L/km.
- Calculate how much fuel the truck needs to travel 20Â km.
\begin{align} \frac{\text{volume of fuel}}{20 \text{ km}} &= \frac{1}{8} \\ \frac{20}{1}\times \frac{\text{volume}}{20} &= \frac{1}{8} \times \frac{20}{1} \\ \text{volume}&=\frac{20}{8} \\ &=\frac{5}{2}\text{ L or } 2.5\text{ L} \end{align}
- Calculate how far the truck can travel with 20Â litres of fuel.
\begin{align} \frac{20\text{ L}}{ \text{distance}} &= \frac{1}{8} \\ \frac{1}{20}\times \frac{20}{\text{distance}} &= \frac{1}{8} \times \frac{1}{20} \\ \frac{1}{\text{distance}}&=\frac{1}{160} \\ \therefore \text{distance}&=160\text{ km} \end{align}
-
In a factory that produces tinned milk powder, a machine is used to put lids on the tins. The table of values shows the production rate of the machine.
\begin{array}{|l|c|c|c|} \hline \text{Time in minutes } (t) & 2 & 4 & 6 \\ \hline \text{Number of lids }(N) & 30 & 60 & 90 \\ \hline \end{array}- Calculate the proportionality constant for the relationship between number of lids and time.
\begin{align} \frac{N}{t} &= \frac{30}{2} \\ &=15 \end{align}
You can use any pair of values from the table.
- What does the proportionality constant represent?
It represents the production rate of the machine, which is 15 lids/min.
- Write an equation for the relationship between number of lids and time.
- Draw a graph of number of lids versus time.
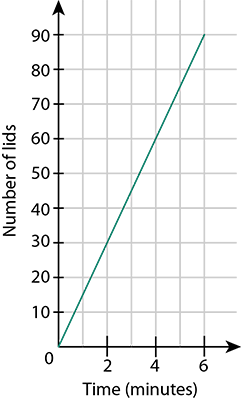
-
The principal wants to cover a rectangular area of the schoolyard with concrete blocks. Each block is 1Â m 1Â m. The available area has a fixed breadth. The length of the area that will be covered depends on how many blocks the school can afford.
- The principal works out that she needs 360 blocks if she wants to cover an area with a length of 20Â m. Calculate the fixed breadth of the available area.
The number of blocks needed is equal to the area of the rectangle, because one block has an area of 1Â m .
\begin{align} A &= l \times b \\ 360 &= 20 \times b \\ \frac{360}{20}&=\frac{20b}{20} \\ b&=18\text{ m} \end{align}- Write an equation for the relationship between the number of blocks needed and the length of the area that can be covered.
- Explain why the number of blocks is directly proportional to the length of the area to be covered.
The breadth is fixed, so the ratio of to is constant.
- If the school can afford 635 blocks, calculate the maximum length that can be covered.
\begin{align} N&=18l \\ 635&=18l \\ \frac{635}{18}&=\frac{18l}{18} \\ \therefore l&=35.28 \end{align}
The maximum length that can be covered is 35Â m, because each block is 1Â m long. The last 0.28Â m cannot be covered.
Inverse proportion
An inverse proportion is a relationship between two variable quantities such that one quantity increases in the same ratio as the other decreases. The one quantity is a constant multiple of the reciprocal of the other. This means the product of the two quantities is a constant. We say the quantities are inversely proportional to each other.
If is inversely proportional to , we write in symbols:
Because the one quantity is a constant multiple of the reciprocal of the other, we can write:
The value of remains constant and is called the proportionality constant.
We can rearrange the equation as follows:
This shows that the product of and is a constant.
inverse proportion An inverse proportion is a relationship between two variable quantities such that one quantity increases in the same ratio as the other decreases. This means one quantity is a constant multiple of the reciprocal of the other.
inversely proportional Two variable quantities are inversely proportional if one quantity increases in the same ratio as the other decreases.
proportionality constant In an inverse proportion, the proportionality constant is the constant product of two variable quantities.
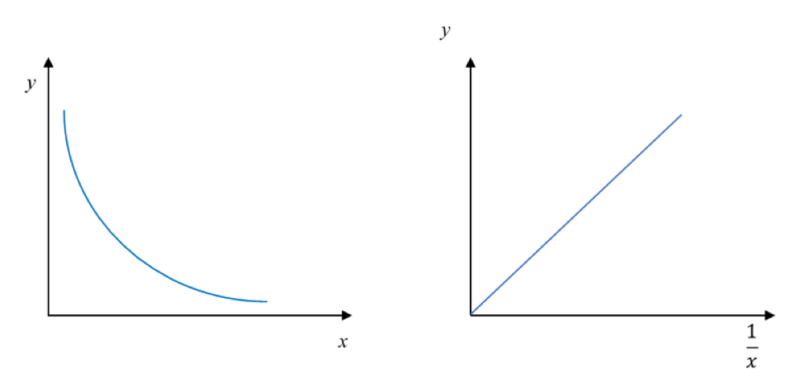
In inverse proportion, graphs of versus and versus look like this:
Worked example 1.13: Applying an inverse proportion
An amount of gas is put in a closed syringe at a constant temperature. The plunger of the syringe is used to change the pressure and volume of the gas. The following table of values give some of the readings.
\begin{array}{|l|c|c|c|c|} \hline \text{Pressure in kPa } (p) & 100 & 120 & 150 & 200 \\ \hline \text{Volume in cm}^3\;(V) & 30 & 25 & 20 & 15 \\ \hline \end{array}
- Determine whether the pressure and volume are directly proportional or inversely proportional to each other.
- Calculate the proportionality constant.
- Write an equation for the relationship between pressure and volume.
-
Step 1: If the two variables are directly proportional, their ratio must be constant. If the two variables are inversely proportional, their product must be constant.
From the table of values:
\begin{align} \frac{p}{V}&=\frac{100}{30}=3.33 \\ \frac{p}{V}&=\frac{120}{25}=4.8 \\ \frac{p}{V}&=\frac{150}{20}=7.5 \\ \frac{p}{V}&=\frac{200}{15}=13.33 \\ \end{align}The ratio is not constant, so is not directly proportional to .
From the table of values:
\begin{align} pV&=(100)(30)=3,000 \\ pV&=(120)(25)=3,000 \\ pV&=(150)(20)=3,000 \\ pV&=(200)(15)=3,000 \\ \end{align}The product is constant, so is inversely proportional to .
-
Step 2: The proportionality constant is the constant product of the two variables.
In this case, .
-
Step 3: Pressure is a constant multiple of the reciprocal of volume. This means the product of the pressure and the volume is constant.
The equation is:
\begin{align} p&=3,000 \times \frac{1}{V}\\ p&=\frac{3,000}{V} \end{align}or
Exercise 1.12: Apply inverse proportion
-
The relationship between the density and volume of different materials is investigated. Exactly the same mass of each material is used. The table of values show some of the readings.
\begin{array}{|l|c|c|c|c|} \hline \text{Density in g/ml } (D) & 0.25 & 0.5 & 1 & 1.6 \\ \hline \text{Volume in ml }(V) & 4 & 2 & 1 & 0.625 \\ \hline \end{array}- Calculate the proportionality constant for the relationship between density and volume.
\begin{align} DV &= (0.25)(4) \\ &=1 \end{align}
You can use any pair of values from the table.
- Write an equation for the relationship between density and volume.
\begin{align} D&=1 \times \frac{1}{V}\\ D&=\frac{1}{V} \end{align}
or
- What do you think the proportionality constant represents?
It represents the mass that was used: 1Â g.
- Calculate the density of a material with a mass of 1Â g and a volume of 2.5Â ml.
\begin{align} D&=1 \times \frac{1}{V}\\ D&=\frac{1}{2.5} \\ &=0.4\text{ g/ml} \end{align}
-
In an electric circuit, current is inversely proportional to resistance . In a certain circuit, the current is 2 amperes when the resistance is 6 ohms.
- Calculate the proportionality constant for the relationship between current and resistance.
\begin{align} IR &= (2)(6) \\ &=12 \end{align}
- Write an equation for the relationship between current and resistance.
\begin{align} I&=12 \times \frac{1}{R}\\ I&=\frac{12}{R} \end{align}
or
- If the resistance in the circuit is increased to 8 ohms, what will the new current be?
\begin{align} I&=\frac{12}{R} \\ &=\frac{12}{8}\\ &=1.5\text{ amperes} \end{align}
- If the resistance in the circuit is doubled, what will happen to the current?
The current will decrease in the same ratio, so it will halve.
-
The force between two spheres is inversely proportional to the square of the distance between their centres . For two specific spheres, the proportionality constant is 4.
- Write an equation for the relationship between force and square of distance.
\begin{align} F&=4 \times \frac{1}{r^2}\\ F&=\frac{4}{r^2} \end{align}
or
- If the value of the square of the distance is 9, calculate the value of the force.
\begin{align} F&=\frac{4}{r^2} \\ &=\frac{4}{9}\text{ or } 0.44\\ \end{align}
- If the value of the force is 0.25, calculate the value of the square of the distance.
\begin{align} Fr^2&=4 \\ (0.25)r^2&=4\\ \frac{0.25r^2}{0.25}&=\frac{4}{0.25}\\ r^2&=16 \end{align}
- If the value of the force is 0.16, calculate the value of the distance between the centres of the spheres.
The question asks for the distance, not the square of the distance.
\begin{align} Fr^2&=4 \\ (0.16)r^2&=4\\ \frac{0.16r^2}{0.16}&=\frac{4}{0.16}\\ r^2&=25\\ \therefore r&= \sqrt{25} \\ &= 5 \end{align}
1.6 Compound interest
Last year you learnt that interest is extra money you pay on a loan or money you earn on an investment. A loan is an amount of money you borrow, that you must normally pay back with interest. An investment is an amount of money you give to a business or bank in the hope of getting more money back.
interest Interest is extra money you pay on a loan or money you earn on an investment.
loan A loan is an amount of money you borrow, that you must normally pay back with interest.
investment An investment is an amount of money you give to a business or bank in the hope of getting more money back.
Revision of simple interest
When you take out a loan or make an investment, the original amount of money you borrow or invest is called the principal amount (P). Last year you worked with simple interest. This is interest that is calculated as a percentage of the principal amount. The interest rate (i) is the percentage of the principal amount that you pay or earn per specified time period. The number of time periods (n) is the number of months or years over which your loan or investment runs. The actual amount (A) is the actual amount of money you pay back or get out. It is the principal amount plus the simple interest.
We calculate simple interest as follows:
We calculate the actual amount as follows:
\begin{align} A &= P+SI \\ \therefore A&=P + P\times i \times n \\ \text{or } A&=P(1+in) \end{align}principal amount (P) The principal amount is the original amount of money borrowed when a loan is taken out, or paid in when an investment is made.
simple interest (SI) Interest that is calculated as a percentage of the principal amount is called simple interest.
interest rate (i) For simple interest, the interest rate on the loan or investment is the percentage of the principal amount that you pay or earn per specified time period.
number of time periods (n) The number of time periods is the number of months or years over which a loan or an investment runs.
actual amount (A) The actual amount is the actual amount of money you pay back on a loan or get out from an investment. It is the principal amount plus the simple interest.
Worked example 1.14: Calculating simple interest and actual amount
A person invests ₦50,000 in a fixed deposit account with an interest rate of 8% per annum. Calculate the interest earned over 5 years, as well as the balance of the account at the end of the 5 years.
The phrase "per annum" means per year.
-
Step 1: Make a list of the symbols A, P, SI, i, n. Insert the information you have next to each symbol. Write a question mark next to the symbol(s) you have to calculate.
\begin{align} A&=\,? \\ P&=₦50,000 \\ SI &=\, ? \\ i&=8 \% \\ n&=5 \end{align} -
Step 2: Write down the applicable formula(e).
For simple interest:
For the actual amount:
-
Step 3: Substitute the values you have and calculate the answer(s).
Remember that a percentage is a fraction:
The simple interest is:
\begin{align} SI&=P \times i \times n \\ &= ₦50,000 \times 8\% \times5 \\ &= ₦250,000 \times 8\% \\ &=₦250,000 \times \frac{8}{100} \\ &=₦20,000 \end{align}The actual amount is:
\begin{align} A&=P + SI \\ &= ₦50,000 + ₦20,000 \\ &= ₦70,000 \end{align}
Exercise 1.13: Revise calculations related to simple interest
-
Calculate the interest due on a loan of ₦60,000 to be repaid over 6 years at an interest rate of 8% per annum.
\begin{align} SI&=P \times i \times n \\ &= ₦60,000 \times 8\% \times6 \\ &=₦360,000 \times \frac{8}{100} \\ &=₦28,800 \end{align}
-
Calculate the total amount of money paid back over 5 years on a loan of ₦25,000 with an interest rate of 15% per annum.
\begin{align} A&=P(1+in) \\ &= ₦25,000(1 + 15\% \times5) \\ &= ₦25,000 (1 + \frac{15}{100} \times 5) \\ &= ₦25,000 (\frac{100}{100} + \frac{75}{100}) \\ &=₦25,000 \times\frac{175}{100} \\ &=₦43,750 \end{align}
-
If a bank offers an interest rate of 10% per annum, for how long must you invest ₦15,000 if you want it to increase to ₦25,500?
\begin{align} A&=P(1+in) \\ A&=P+Pin \\ A-P&=Pin \\ n&=\frac{A-P}{Pi} \\ &=\frac{₦25,500-₦15,000}{₦15,000\times \frac{10}{100}} \\ &=\frac{₦10,500}{₦1,500} \\ &=7\text{ years} \end{align}
-
The total repayments on a loan add up to ₦325,600 after 4 years. If the interest rate is 12% per annum, calculate the original amount of money borrowed.
\begin{align} A&=P(1+in) \\ P&=\frac{A}{1+in} \\ &=\frac{₦325,600}{1+12\%\times 4} \\ &=\frac{₦325,600}{100\%+48\%} \\ &=\frac{₦325,600}{\frac{148}{100}} \\ &=₦325,600 \times \frac{100}{148} \\ &=₦220,000 \end{align}
-
Calculate the annual interest rate offered by a bank where a deposit of ₦75,000 increases to ₦87,000 in 4 years.
The phrase "annual interest rate" means the interest rate per year.
\begin{align} A&=P(1+in) \\ A&=P+Pin \\ A-P&=Pin \\ i&=\frac{A-P}{Pn} \\ &=\frac{₦87,000-₦75,000}{₦75,000\times 4} \\ &=\frac{₦12,000}{₦300,000} \\ &=\frac{2}{50}\\ &=\frac{4}{100} \\ &=4\% \end{align}
Definition and formula for compound interest
Simple interest is calculated on only the principal amount, which is the original amount of money you borrowed or invested. Compound interest, however, can be described as interest charged on interest. The amount used to calculate the interest changes as an investment grows or a loan is paid off. This influences the actual amount.
compound interest Compound interest is interest that is calculated on both the original amount of money borrowed or invested, and the interest that has been earned or paid over time.
The formula we use to calculate the actual amount when there is compound interest on a loan or an investment is:
The meanings of the symbols are the same as before:
- is the total amount including interest, called the actual amount
- is the original amount borrowed or invested, called the principal amount
- is the interest rate expressed as a percentage
- is the number of periods
To calculate only the interest, excluding the principal amount, remember:
Remember that a percentage is a fraction, for example
Do not confuse the formulae for simple interest and compound interest.
- For simple interest:
- For compound interest:
Calculations related to compound interest
Worked example 1.15: Calculating compound interest and actual amount
A person invests ₦50,000 in a fixed deposit account with an interest rate of 8% per annum. Compound interest is added every 6 months. Calculate the balance of the account and interest earned after 5 years.
If interest is added every 6 months, it is added twice a year.
-
Step 1: Make a list of the symbols A, P, i, n. Insert the information you have next to each symbol. Write a question mark next to the symbol(s) you have to calculate.
\begin{align} A&=\,? \\ P&=₦50,000 \\ i&=8 \% \text{ per year } = 4\% \text{ per six months}\\ n&=5\times2 = 10 \end{align} -
Step 2: Write down the applicable formula.
For compound interest:
-
Step 3: Substitute the values you have and calculate the answer(s).
\begin{align} A&=P(1+i)^n \\ &= ₦50,000\Big(1+\frac{4}{100}\Big)^{10} \\ &= ₦50,000\Big(\frac{100}{100}+\frac{4}{100}\Big)^{10} \\ &= ₦50,000\Big(\frac{104}{100}\Big)^{10} \\ &=₦74,012.21 \end{align}The interest earned is:
\begin{align} \text{Interest }&=A-P \\ &= ₦74,012.21-₦50,000 \\ &= ₦24,012.21 \end{align}
Worked example 1.16: Calculating principal amount
A person invested an amount at 5% per annum for 3 years. Compound interest was added every year. At the end of the 3 years, the value of the investment was ₦17,250. Calculate the principal amount that was invested.
-
Step 1: Make a list of the symbols A, P, i, n. Insert the information you have next to each symbol. Write a question mark next to the symbol(s) you have to calculate.
\begin{align} A&=₦17,250 \\ P&=\,? \\ i&=5 \% \text{ per year } \\ n&=3 \end{align} -
Step 2: Write down the applicable formula.
For compound interest:
-
Step 3: Substitute the values you have and calculate the answer(s).
\begin{align} A&=P(1+i)^n \\ ₦17,250&= P\Big(1+\frac{5}{100}\Big)^3 \\ ₦17,250&= P\Big(\frac{100}{100}+\frac{5}{100}\Big)^3 \\ ₦17,250&= P\Big(\frac{105}{100}\Big)^3 \\ \Big(\frac{100}{105}\Big)^3\times₦17,250 &= P\Big(\frac{105}{100}\Big)^3 \times \Big(\frac{100}{105}\Big)^3\\ P&=₦14,901.20\end{align}
Worked example 1.17: Calculating a loan balance
A person takes out a loan of ₦20,000 that has an annual compound interest rate of 12%. He repays ₦5,000 per year. Calculate the balance of the loan at the end of the second year.
Because there are repayments at the end of each year, we have to do a calculation for every year.
-
Step 1: Calculate the balance at the end of the first year before any repayments.
\begin{align} A&=P(1+i)^n \\ &=₦20,000\Big(1+\frac{12}{100}\Big)^1 \\ &=₦20,000 \times\frac{112}{100} \\ &=₦22,400 \end{align} -
Step 2: Subtract the repayments.
-
Step 3: Repeat Steps 1 and 2 for the second year.
\begin{align} A&=P(1+i)^n \\ &=₦17,400\Big(1+\frac{12}{100}\Big)^1 \\ &=₦17,400 \times\frac{112}{100} \\ &=₦19,488 \end{align} \begin{array}{r} ₦19,488 \newline -\,₦5,000 \newline \hline ₦14,488\newline \hline \end{array}
Exercise 1.14: Do calculations related to compound interest
-
Calculate the total amount of money that will be owed to the bank after 5 years on a loan of ₦75,000 with a compound interest rate of 15% per annum, if no repayments were made.
\begin{align} A&=P(1+i)^n \\ &= ₦75,000\Big(1+\frac{15}{100}\Big)^{5} \\ &= ₦75,000\Big(\frac{115}{100}\Big)^{5} \\ &=₦150,851.79 \end{align}
-
An amount of ₦40,000 is invested for 4 years. Compound interest of 12% per annum is added monthly. Calculate the value of the investment at the end of the 4 years.
If interest is added monthly, and per month.
\begin{align} A&=P(1+i)^n \\ &= ₦40,000\Big(1+\frac{1}{100}\Big)^{48} \\ &= ₦40,000\Big(\frac{101}{100}\Big)^{48} \\ &=₦64,489.04 \end{align} -
Compound interest of 16% per year is added every 3 months to a loan of ₦20,000. If no repayments are made during the first 2 years, calculate the interest added to the loan over the 2 years.
If interest is added every 3 months, it is added 4 times a year. Therefore and per 3 months.
\begin{align} A&=P(1+i)^n \\ &= ₦20,000\Big(1+\frac{4}{100}\Big)^{8} \\ &= ₦20,000\Big(\frac{104}{100}\Big)^{8} \\ &=₦27,371.38 \end{align} \begin{align} \text{Interest }&=A-P \\ &= ₦27,371.38-₦20,000 \\ &= ₦7,371.38 \end{align} -
The balance of an investment is ₦29,440.96 after annual compound interest of 6% was added yearly for 5 years. What amount of money was invested?
\begin{align} A&=P(1+i)^n \\ ₦29,440.96&= P\Big(1+\frac{6}{100}\Big)^5 \\ ₦29,440.96&= P\Big(\frac{106}{100}\Big)^5 \\ \Big(\frac{100}{106}\Big)^5\times₦29,440.96 &= P\Big(\frac{106}{100}\Big)^5 \times \Big(\frac{100}{106}\Big)^5\\ P&=₦22,000\end{align}
-
The compound interest rate on a hire purchase amount of ₦5,000 is 20% per annum. Interest is added every 6 months, after which the customer makes a repayment of ₦1,500. Calculate the balance of the account at the end of the first year.
If interest is added every 6 months, it is added twice a year. Therefore for 6 months.
At the end of the first 6 months:
\begin{align} A&=P(1+i)^n \\ &=₦5,000\Big(1+\frac{10}{100}\Big)^1 \\ &=₦5,000 \times\frac{110}{100} \\ &=₦5,500 \\ \end{align} \begin{array}{r} ₦5,500 \newline -\,₦1,500 \newline \hline ₦4,000\newline \hline \end{array}At the end of the first year:
\begin{align} A&=P(1+i)^n \\ &=₦4,000\Big(1+\frac{10}{100}\Big)^1 \\ &=₦4,000 \times\frac{110}{100} \\ &=₦4,400 \\ \end{align} \begin{array}{r} ₦4,400 \newline -\,₦1,500 \newline \hline ₦2,900\newline \hline \end{array}
1.7 Summary
- The base ten number system or decimal number system is a number system that counts in groups of 10, and uses the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 to represent any number.
- The base two number system or binary number system is a number system that counts in groups of 2, and uses only the digits 0 and 1 to represent any number.
- We use subscripts to tell us which number base system a certain combination of digits belong to. For example:
- or means
- or means
- or means
- We can convert numbers from one number system to another:
- We start with the powers of the given base and convert the given number to a decimal number.
- We then convert the decimal number to the required number system by working with the powers of the required base.
- We can use algebraic expressions and equations to interpret and solve word problems.
- We expand an algebraic expression by using the distributive law to remove brackets and then collecting like terms.
- The distributive law states that the multiplying factor or coefficient of a bracket can be distributed across each of the terms inside the bracket, for example .
- Sometimes it is necessary to factorise part of an algebraic expression before we can simplify it. Factorising an algebraic expression is the reverse of expanding it.
- A direct proportion is a relationship between two variable quantities of which the ratio is constant because the one quantity is a constant multiple of the other.
- Two variable quantities are directly proportional if their ratio is constant because the one quantity is a constant multiple of the other.
- An inverse proportion is a relationship between two variable quantities such that one quantity increases in the same ratio as the other decreases.
- Two variable quantities are inversely proportional if their ratio is constant because the one quantity is a constant multiple of the reciprocal of the other quantity.
- A proportionality constant is the constant ratio of one variable quantity to another or the constant product of two variable quantities.
- Interest is extra money you pay on a loan or money you earn on an investment.
- Interest that is calculated as a percentage of the principal amount is called simple interest.
- Compound interest is interest that is calculated on both the original amount of money borrowed or invested, and the interest that has been earned or paid over time.
- We use these formulae to calculate interest:
- Simple interest:
- Compound interest:
